En este post les dejo un notebook de Mathematica, en el cual les muestro cómo explotar la potencia de esta herramienta de cálculo simbólico (y numérico!) para resolver problemas de flujos potenciales bidimensionales.
En particular, el notebook trata un problema ya conocido por ustedes: el flujo alrededor de un cilindro con una circulación atrapada que enfrenta un flujo uniforme al infinito.
La idea detrás de este post es que tengan una guía de cómo resolver y analizar este ejercicio en Mathematica, teniendo en cuenta que ustedes conocen ya la física del problema, cuyo detalle discutimos en clase practica. El propósito subyacente es que, si así lo desean, puedan extrapolar lo que aprendan aquí a la resolución de cualquier otro problema de la guía.
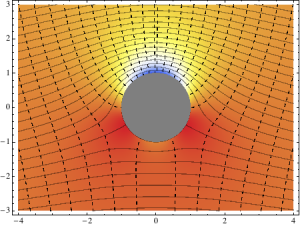
Curvas de nivel de la función corriente (trazo continuo), de potencial (líneas punteadas) y campo de presiones (en color) para un caso particular de los parámetros del problema.
Sólo a modo de sumario, les cuento qué tipo de cálculos aprenderán a hacer en Mathematica usando este notebook. Entre otras cosas, verán cómo: (i) definir un potencial complejo, (ii) aplicar el teorema del círculo de Milne-Thomson, (iii) determinar las funciones potencial y de corriente, (iv) calcular los campos de velocidad, (v) obtener el campo de presiones en todo punto del espacio usando el teorema de Bernoulli y (vi) calcular la fuerza sobre el obstáculo mediante: (a) la integral de presión sobre el contorno sólido y (b) el teorema de Blasius via el cálculo de residuos. Asimismo, podran ver como se representan usualmente en forma grafica cada uno de estos resultados y como generar dichos graficos en Mathematica.
El archivo/notebook de Mathematica podrán descargarlo (tanto en formato Mathematica como en formato PDF, para quienes no disponen del software) haciendo click derecho aquí y descomprimiendo el archivo .zip que descargaran.
Espero que les sirva.

