En la clase del martes 26 vimos que para una cuerda con N cuentas idènticas equiespaciadas hay infinitos valores discretos de la constante θ que satisfacen las condiciones para modos transversales con extremos fijos. Pero estos infinitos valores discretos tienen que representar sólo N modos distintos, no? Claro, eso es lo que habríamos obtenido si hubiéramos diagonalizado la matriz del sistema.
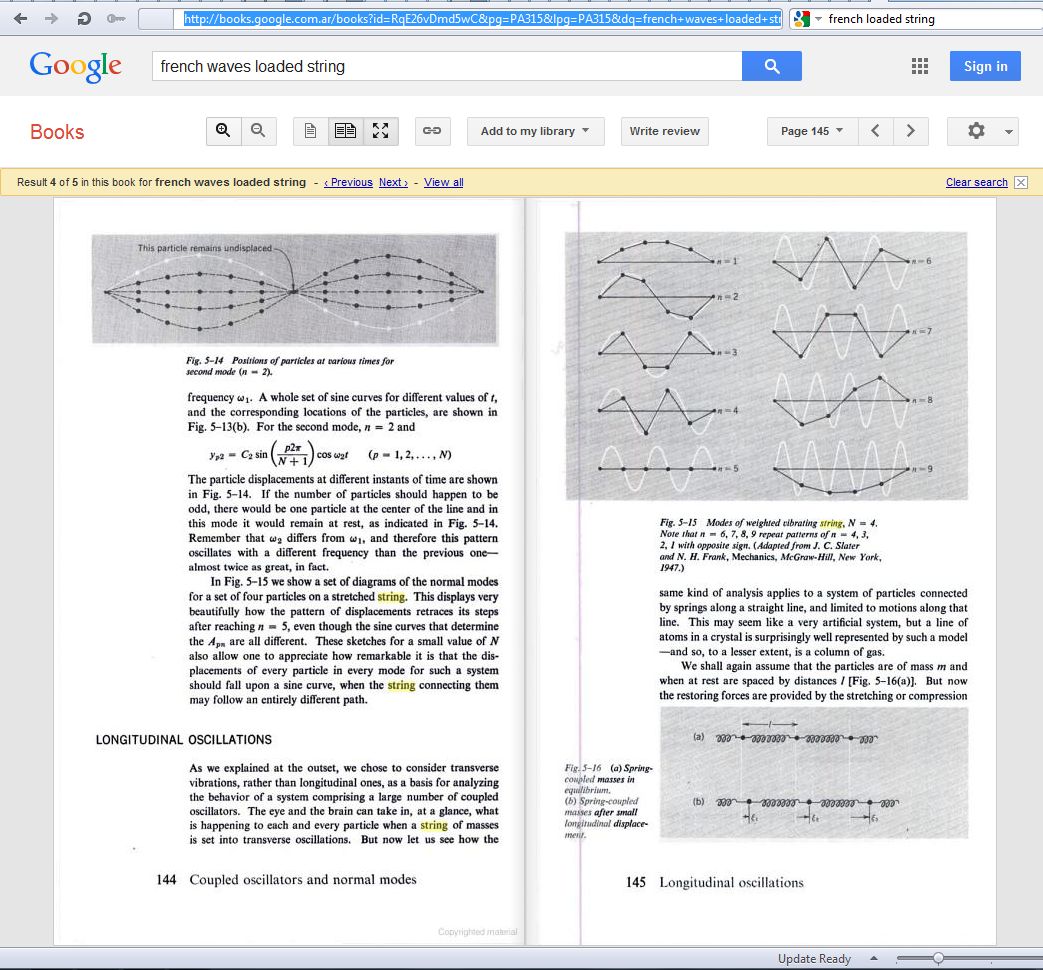
Para que quede claro que los valores de θ sub p, con p mayor que N, representan físicamente los mismos modos que los obtenidos para valores de p entre 1 y N, miren la Figura 5.15 del libro “Vibrations and Waves” de A. P. French. El libro (incompleto) está en Google Books, acá les dejo una captura de pantalla de las páginas 144 y 145 (click para ampliar)
La figura 5.15 muestra un sistema con N=4 (ojo, el n de la figura corresponde al p usado en clase). En la columna de la izquierda se ven los modos para p=1, 2, 3, 4 y 5. Claramente la solución para p=5 describe el equilibrio, igual que la solución para p=0. Y lo más importante: observen que el modo con p=6 es físicamente indistinguible del modo con p=4, que el modo con p=7 es físicamente indistinguible del modo con p=3, etc. O sea: tal como ya sabíamos hay N modos, a pesar de que hay infinitos valores de θ que satisfacen la condición de contorno que escribimos en clase. La demostración matemática para cualquier valor de N está en las páginas 142 y 143 (también en Google Books).
Para ir pensando y comentar en este post antes del próximo viernes: ¿Qué constantes quedaron sin determinar? ¿Cómo se escribe el movimiento más general del sistema?

 Follow
Follow