En la clase del martes 26 vimos que para una cuerda con N cuentas idènticas equiespaciadas hay infinitos valores discretos de la constante θ que satisfacen las condiciones para modos transversales con extremos fijos. Pero estos infinitos valores discretos tienen que representar sólo N modos distintos, no? Claro, eso es lo que habríamos obtenido si hubiéramos diagonalizado la matriz del sistema.
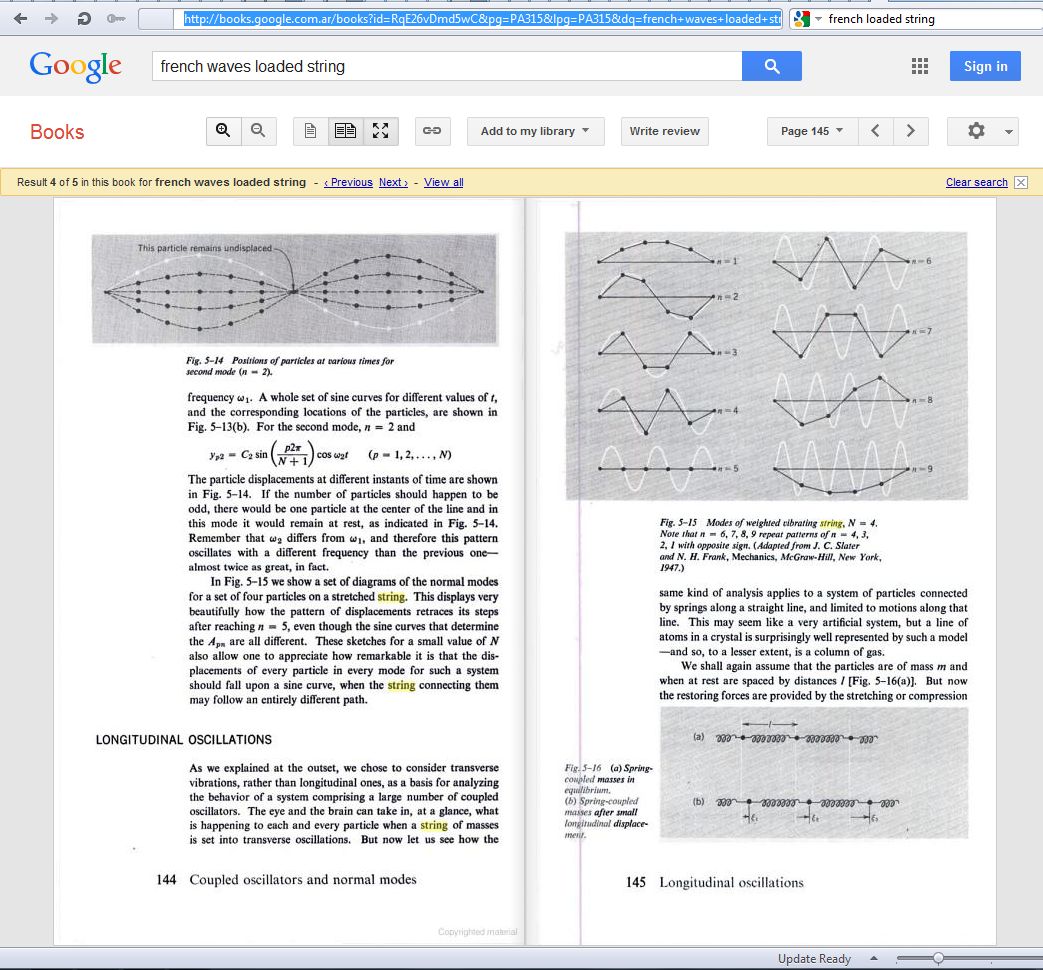
Para que quede claro que los valores de θ sub p, con p mayor que N, representan físicamente los mismos modos que los obtenidos para valores de p entre 1 y N, miren la Figura 5.15 del libro “Vibrations and Waves” de A. P. French. El libro (incompleto) está en Google Books, acá les dejo una captura de pantalla de las páginas 144 y 145 (click para ampliar)
La figura 5.15 muestra un sistema con N=4 (ojo, el n de la figura corresponde al p usado en clase). En la columna de la izquierda se ven los modos para p=1, 2, 3, 4 y 5. Claramente la solución para p=5 describe el equilibrio, igual que la solución para p=0. Y lo más importante: observen que el modo con p=6 es físicamente indistinguible del modo con p=4, que el modo con p=7 es físicamente indistinguible del modo con p=3, etc. O sea: tal como ya sabíamos hay N modos, a pesar de que hay infinitos valores de θ que satisfacen la condición de contorno que escribimos en clase. La demostración matemática para cualquier valor de N está en las páginas 142 y 143 (también en Google Books).
Para ir pensando y comentar en este post antes del próximo viernes: ¿Qué constantes quedaron sin determinar? ¿Cómo se escribe el movimiento más general del sistema?


 Follow
Follow
No sé cuales son esas constantes que quedaron sin determinar. El movimiento mas general del sistema se va a escribir como la multiplicación de dos cosenos con una amplitud. Un coseno que representa el espacio y otro el temporal. El espacial es el que va a depender de tita y tendrá una fase espacial y el coseno espacial dependiente de la frecuencia del modo excitado, del tiempo y de una fase temporal. No es así?. Sin embargo, esta representación es teniendo en cuenta hay distancia entre los cuerpos discretos. Habría que ver cómo la adaptamos para que funcione también para cuando la distancia tiende a cero y los cuerpos al infinito y se pueda considerar ahora sí como una onda propiamente dicha.
Tengo una pregunta para hacer. En la figura que usted cita la 5-15 se ve que “los modos se repiten” para distintos titas y esos titas son los que producen los armónicos, no? Entonces, al tocar por ejemplo la guitarra al ir poniendo los dedos se efectuan distintos armónicos tomando los distintos titas. Entonces es posible que en una misma cuerda con dos digitaciones distintas obtengamos la misma frecuencia, es decir la misma nota?
Saludos
Hola Romina, qué bueno que comentes en la página!!
Con respecto a lo de “poner los dedos” sobre una cuerda de guitarra (apretándola contra el mástil), lo que se logra es cambiar la longitud de la cuerda. En cambio, la tensión de cada cuerda se fija afjojando o ajustando el clavijero, como mostró Marcos, tu compañero que justo tenía su guitarra en la clase del martes pasado. Pero una vez fijada la longitud de la cuerda, los modos que intervienen en su movimiento dependen esencialmente de la condición inicial. Esto lo veremos con mas detalle en la clase de mañana.
Con respecto a los modos que se repiten en la figura 5-15, hay que convencerse de que los modos de la columna izquierda son indistinguibles físicamente de los modos de la columna derecha. Representan la misma situación física, es decir que ningún experimento que hagas te permitiría decir si estás en el modo de la columna izquierda (con un valor de tita) o en el modo de la columna derecha (con el valor pi menos tita).
Saludos!
No me había dado cuenta de esa distintición de la tensión de la cuerda y la longitud, interesante. En que influye la tensión de la cuerda?