Cuando se perturba la superficie de un líquido en equilibrio aparecen dos fuerzas restitutivas, la gravedad y la tensión superficial. Según cuál sea la fuerza restitutiva que predomina, se obtienen dos tipos de onda, las ondas de gravedad (como las olas producidas por el viento) o las ondas capilares. Les dejo un video donde se pueden visualizar las ondas capilares y las ondas de gravedad y donde además se discuten la dispersión “normal” versus la dispersión “anómala”.
El Puente del Milenio es un puente colgante que cruza el río Támesis. Se inauguró el 10 de junio del año 2000 y fue todo un acontencimiento, porque hacía mucho que en Londres no se construía un puente sobre el Támesis. El anterior fue el famoso Tower Bridge (Puente de la Torre) en 1894. Pueden hacer un paseo virtual con el Street View de Google Maps, dejo una captura de pantalla 
Debido a unas inesperadas vibraciones, el puente tuvo que ser cerrado dos días después de su apertura. Las primeras vibraciones obligaron a los transeúntes a caminar de manera sincronizada con el balanceo y esta sincronización aumentó el efecto. Hay un documental de la BBC sobre el tema, donde se pueden ver los movimientos del día de la inauguración (click en la imagen para reproducir un fragmento del documental)
Pregunta para el final: ¿Es correcto decir que la frecuencia natural del modo de torsión es parecida a la frecuencia del paso de los peatones?
Como se ve en este video (click en la imagen)
hay gente que se ocupa de excitar modos de vibraciòn de puentes colgantes, tanto los modos longitudinales (análogos a los de la cuerda) como los modos de torsión (los que dieron problemas a los ingenieros del Puente del Milenio).
Cuatro enlaces para saber más sobre el tema del puente:
En la clase del martes 26 vimos que para una cuerda con N cuentas idènticas equiespaciadas hay infinitos valores discretos de la constante θ que satisfacen las condiciones para modos transversales con extremos fijos. Pero estos infinitos valores discretos tienen que representar sólo N modos distintos, no? Claro, eso es lo que habríamos obtenido si hubiéramos diagonalizado la matriz del sistema.
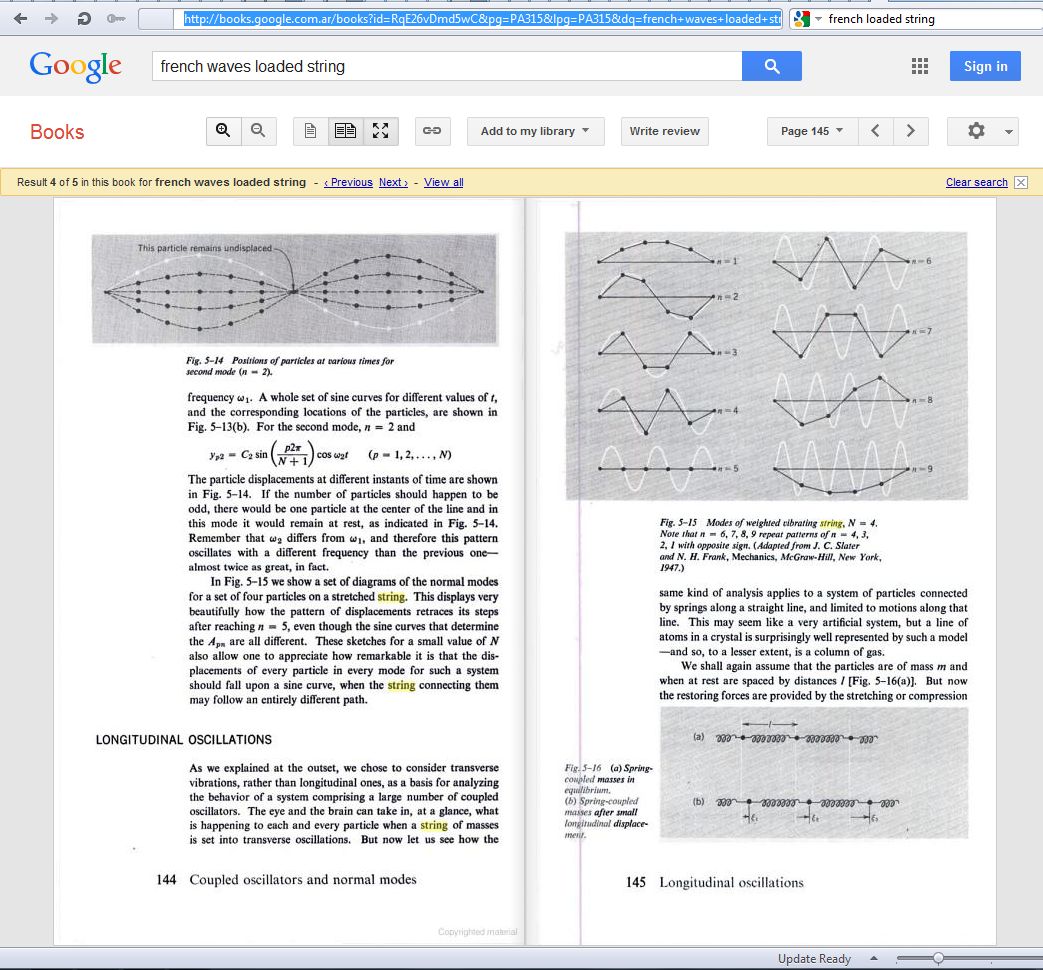
Para que quede claro que los valores de θ sub p, con p mayor que N, representan físicamente los mismos modos que los obtenidos para valores de p entre 1 y N, miren la Figura 5.15 del libro “Vibrations and Waves” de A. P. French. El libro (incompleto) está en Google Books, acá les dejo una captura de pantalla de las páginas 144 y 145 (click para ampliar)
La figura 5.15 muestra un sistema con N=4 (ojo, el n de la figura corresponde al p usado en clase). En la columna de la izquierda se ven los modos para p=1, 2, 3, 4 y 5. Claramente la solución para p=5 describe el equilibrio, igual que la solución para p=0. Y lo más importante: observen que el modo con p=6 es físicamente indistinguible del modo con p=4, que el modo con p=7 es físicamente indistinguible del modo con p=3, etc. O sea: tal como ya sabíamos hay N modos, a pesar de que hay infinitos valores de θ que satisfacen la condición de contorno que escribimos en clase. La demostración matemática para cualquier valor de N está en las páginas 142 y 143 (también en Google Books).
Para ir pensando y comentar en este post antes del próximo viernes: ¿Qué constantes quedaron sin determinar? ¿Cómo se escribe el movimiento más general del sistema?
a pedido de varios alumnos, la Secretaría del Departamento de Física mantendrá abierta la inscripcion en F2 (turno mañana) hasta el viernes 29 de agosto inclusive.
Este es el título del trabajo publicado en 1728 por Johann Bernoulli donde trata el problema de los modos de vibración de una cuerda con cuentas, el mismo problema que empezamos a ver hoy en clase.
El tema de las cuerdas ya había sido abordado por Brook Taylor (el de la serie). En 1715 Taylor había publicado Methodus incrementorum directa et inversa, donde planteaba los siguientes problemas (que todavía no vimos en clase)
El estudio matemático iniciado por Taylor de la cuerda vibrante dió lugar a una de las controversias más encendidas y más fructíferas en la historia de las matemáticas. El desarrollo del análisis matemático tiene como hilo conductor el deseo de proporcionar respuestas satisfactorias a las muchas preguntas originadas en el estudio de la cuerda vibrante, tal como se discute en el trabajo Impactos del análisis armónico, de Miguel de Guzmán, especialmente en la parte titulada El retorno de los armónicos.
Volviendo a lo que vimos el viernes, les recuerdo que terminamos con una relación entre dos períodos: la cantidad llamada θ, relacionada con un período espacial en nuestro sistema, y ω, la frecuencia angular del modo, relacionada con un período temporal. ¿Qué se puede decir sobre ω como función de θ?
Hacé click en este enlace para bajar un programa Java que simula el comportamiento de dos péndulos acoplados por un resorte. Al ejecutarlo, aparecerá la siguiente pantalla
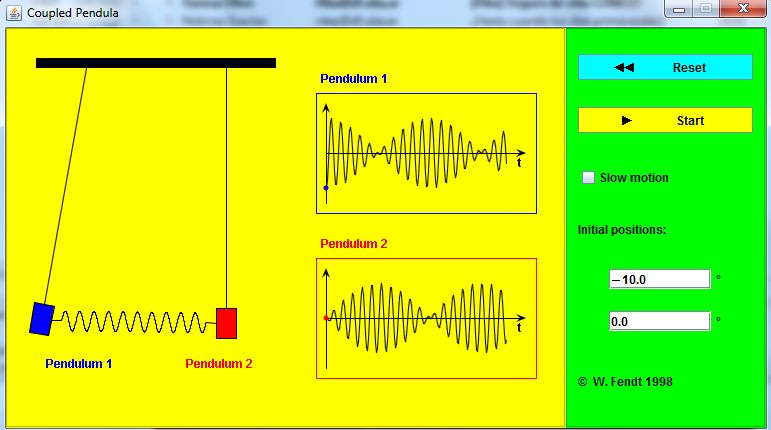
El programa permite elegir las posiciones iniciales de cada parte móvil, (y supone que los péndulos parten del reposo). Indicar qué sucede para las siguientes elecciones:
¿Cuándo hay flujo de energía entre partes móviles? El siguiente video muestra que el flujo de energía entre partes móviles también ocurre para otros acoplamientos
¿Podés explicar el mecanismo que provee el acoplamiento en el caso de este video?
En la clase de hoy hablamos sobre las pulsaciones y batidos que se obtienen al superponer dos oscilaciones armónicas de frecuencias similares. Los escuchamos haciendo sonar simultáneamente dos diapasones de la misma frecuencia nominal. Como aplicación, mencioné el primer instrumento musical electrónico del mundo, el Theremin, un instrumento que no se toca. Fue inventado (en realidad, descubierto por casualidad) por el físico ruso Lev Sergeyevich Termen, conocido en el mundo occidental como Léon Theremin. En este video, Theremin interpreta su propio instrumento
El sonido del theremin se produce por la combinación de las vibraciones de dos osciladores de radio-frecuencia: uno que opera a la frecuencia fija de 170 KHz, y otro que opera a frecuencias variables entre 168 y 170 KHz. El valor exacto de la frecuencia de vibración del segundo oscilador depende de la distancia entre el oscilador y las manos del intérprete. La diferencia entre las frecuencias de los dos osciladores está en el rango entre 0 and 2000 Hz, justamente el rango de frecuencias que corresponde al sonido audible (a la nota más aguda del piano le corresponde una frecuencia de aproximadamente 4200 Hz).
A continuación el video de un músico canadiense que interpreta Get Lucky (tema de Daft Punk) con un theremin sobre un loop de fagot
La primera virtuosa del theremín fue la intérprete Clara Rockmore. Leon se enamoró de Clara y le propuso casamiento, pero fue rechazado (esto no entra para el final). Aquí un video de Clara Rockmore, interpretando “El Cisne”, de Saint-Saëns
Mas info, en inglés, en este video del canal Sixty symbols (gracias Marcos Wappner). Recomiendo un documental excelente sobre la novelesca vida del físico Leon Theremin, se llama Theremin: An Electronic Odyssey.
Para comenzar, te propongo que leas éste artículo de Wikipedia, sobre el funcionamiento de un aparato utilizado en espionaje, que usa luz de un láser para detectar vibraciones sonoras de un objeto distante.
¿Por qué? Porque la luz es una onda. Y el sonido también. Y F2 trata de ondas.
Si entendés muy poco del artículo, no importa. Lo que importa es lo que entiendas cuando vuelvas a leer el mismo artículo al final del cuatrimestre.
Ojalá que entiendas N veces más de lo que entendés ahora!! (con N >> 1).
Para ver cómo hacer un micrófono laser casero, mirá este video
