Los sistemas de cadenas 1D nos conducirán naturalmente a las oscilaciones en cuerdas, un problema que ocupó la mente de grandes matemáticos y músicos de los siglos XVII y XVIII. Entre ellos Daniel Bernoulli, la familia Bach, d’Alembert, Euler y Fourier.
Las cadenas lineales de masas idénticas equiespaciadas hacen su aparición en F2A. El pdf ya está en el campus y la clase grabada en https://t.co/0XjvQA913R pic.twitter.com/HgBtI4scm8
— #F2Depine (@F2Depine_) September 12, 2020
Marcos se despertó fingiendo ser un biólogo especializado en aves y logró captar el canto del zorzal con Spectroid. Lo compartió en Twitter y dió origen a una cadena de tuits muy interesante. Gracias Marcos!
Hacé como Marcos, compartí vos también tu espectro favorito.
Las vocalizaciones en las aves evoluciona en respuesta a una multitud de factores y están también sujetas a la selección natural.
Aporte de @Mardago99 que podemos sumar al desafío de @ChuckleScience
En @Fisica_UBA tenenos a @GaboMindlin un especialista mundial en este tema. https://t.co/vAQLOIhWuy
— #F2Depine (@F2Depine_) September 13, 2020
Había una vez un tiempo en el que se explicaban cosas sin videos ni pdfs. Acá una prueba.
Un hilo sobre batidos y pulsaciones. Con diapasones muy parecidos a los del video que vimos en la clase 4 (incluido en el hilo). Y hay un error, no es el aula 2, es la 4 o la 5 (siempre las confundo).
Dedicada a les alumnes de F2 que aún no conocen el aula 2 del pabellón 1.
Imagen de una clase de #F2Depine de 2018, cuando hicimos sonar diapasones en el aula para ilustrar batidos y pulsaciones. pic.twitter.com/foqEzLeV7A— #F2Depine (@F2Depine_) September 12, 2020
Un hilo con cosas de la Tercera Clase Teórica. No hice a tiempo de bajar todos los espectrogramas que mandaron por el chat de zoom y ahora no los puede recuperar. Sugiero agregarlos al hilo de Twitter o en los comentarios del post, asi vemos los arpegios de Ali o las notas cantadas de Josefina.
Pdf de la Clase 3 en el campus y video en la playlist de F2 del canal de youtube de @Fisica_UBA https://t.co/o1H8hgtW4i pic.twitter.com/rFFJ6HUohj
— #F2Depine (@F2Depine_) September 8, 2020
Al comienzo de la teórica 2 reciclamos el código Python que habíamos hecho en la teórica 1 para un péndulo ideal, para el caso de un péndulo con rozamiento sin la aproximación de ángulos pequeños. Hicimos la simulación numérica con un valor del ángulo inicial igual a 3 radianes (casi coincidente con la vertical) y con un empujón que generaba una velocidad inicial de 10 1/s. En estas condiciones y sin rozamiento, el péndulo se quedaría dando vueltas eternamente. Pero debido a la fuerza de rozamiento, sólo da N vueltas y llega un momento en que el comportamiento del péndulo comienza a ser idéntico al predicho por la aproximación de ángulos pequeños.
En la simulación que vimos en clase, el número de vueltas era N=6. Ahora les dejo el resultado de una simulación con los mismos valores, excepto que bajé el valor del coeficiente de rozamiento. En consecuencia, el número de vueltas aumenta y ahora toma el valor N=11. El gráfico de posición en función del tiempo es el siguiente
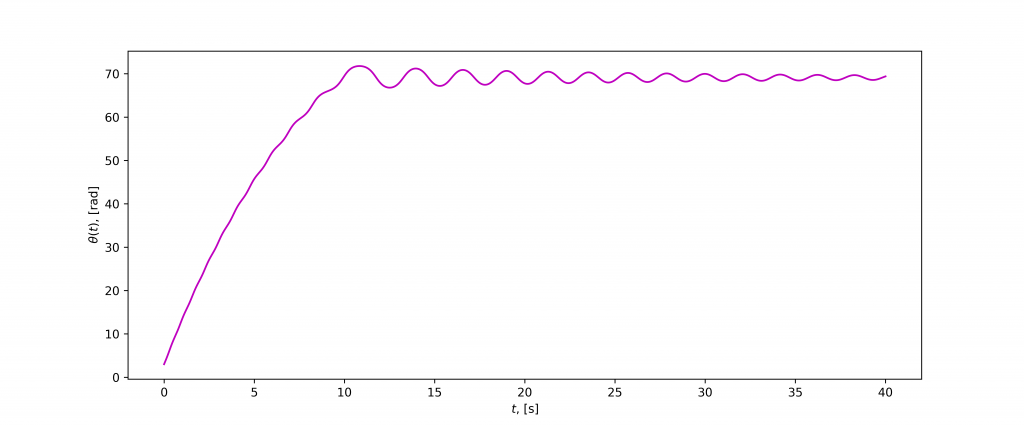
Y para que vean que son 11 vueltas, acá dejo la animación (click en imagen)
El desafío consiste en encontrar las condiciones iniciales para que el péndulo realice N vueltas, con N arbitrario.
“Batido entre dos tonos de frecuencia” es un tema que se estudia en F2. Raro verlo en un mural, no?
Desafío de comienzo del curso del segundo cuatrimestre virtual: ¿en qué lugar de la ciudad de Buenos Aires está este mural? #DesafíoF2 #Batidos pic.twitter.com/nFiy76efPz
— #F2Depine (@F2Depine_) August 30, 2020
