Física 2
Segundo cuatrimestre de 2019
Guía 1: Oscilador armónico

Oscilador armónico de un único grado de libertad

1. Péndulo. Considere un péndulo simple de longitud \(l\) y masa \(m\), tal como se muestra en la figura.

   

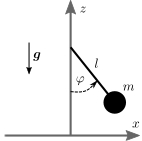
   1. Escriba la ecuación de movimiento del péndulo utilizando las coordenadas: (i) \(x\), \(z\), (ii) \(\varphi\). Escriba la energía potencial y cinética en dichas coordenadas. Discuta cuál elección es más conveniente.

   2. Resuelva la ecuación del péndulo en coordenadas angulares (\(\varphi\)) en la aproximación de pequeñas oscilaciones.

   3. Muestre que en la aproximación de pequeñas oscilaciones la combinación lineal de dos soluciones cualesquiera también es solución. ¿Sigue siendo esto cierto sin las aproximaciones?

   4. Calcule la tensión del hilo en función del ángulo para el péndulo en pequeñas oscilaciones. Discuta la validez de la hipótesis de longitud de hilo constante.

2. Demuestre que si \(\Psi\) es una solución matemática compleja de la ecuación del oscilador armónico, su parte real también es solución.

3. Considere una masa \(m\) sujeta a dos paredes mediante dos resortes iguales de constante \(k\) y longitud natural \(l_0\), tal como se muestra esquematizado en la figura. Inicialmente en equilibrio los resortes tienen una longitud \(l\). Para cada una de las siguientes situaciones, escriba y resuelva las ecuaciones de movimiento del sistema.

   

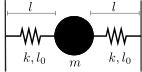
   1. Oscilaciones longitudinales de la masa \(m\).

   2. Oscilaciones transversales de la masa \(m\) (en ausencia de gravedad), para cada uno de los casos límite en que:

      1. la masa se aparta poco respecto de su posición de equilibrio (aproximación de pequeños apartamientos), de forma tal que la longitud del resorte nunca es mucho mayor que \(l\). Analice cuidadosamente las aproximaciones requeridas y describa la diferencia entre considerar que en la posición de equilibrio los resortes están estirados (\(l_{0} < l\)) o que están comprimidos (\(l_0 > l\)) o que están relajados (\(l_{0} = l\)).

      2. el resorte es muy elongable (aproximación “slinky”), de forma tal que puede considerarse \(l_{0} \approx 0\).

      Compare las frecuencias de los modos longitudinales y transversales.

   3. Un desplazamiento general de la masa, tanto longitudinal como transversal, tanto en la aproximación de pequeños desplazamientos como en la aproximación slinky. En particular, muestre que en cualquiera de estas dos aproximaciones los movimientos longitudinales y transversales quedan desacoplados.

4. Escriba y resuelva la ecuación de movimiento de un resorte vertical con un peso colgado usando como cero de coordenadas la longitud del resorte en reposo sin peso. Escriba la energía potencial (gravitatoria más elástica) y encuentre la posición de equilibrio. Analice la curvatura de dicho potencial. Al oscilar, ¿la energía potencial es solo la del resorte o también oscila la potencial gravitatoria?

Oscilador armónico amortiguado

1. Considere una masa \(m\) sujeta a un resorte de constante elástica \(k = m\omega_{0}^{2}\) y en presencia de una fuerza de disipación proporcional a la velocidad con constante de amortiguamiento por unidad de masa \(\Gamma\).

   1. Proponga como solución \(x(t) = C e^{-t/2\tau} \cos\left(\omega_{1}t + \theta\right)\) y halle los valores de \(\tau\) y de \(\omega_{1}\). ¿De qué depende el valor de \(C\) y de \(\theta\)?

   2. Repita el ítem anterior pero ahora proponiendo como solución una función compleja \(x(t) = C e^{\lambda t}\) y halle el valor de \(\lambda\).

   3. Describa bajo qué condiciones sobre \(\Gamma\) y \(\omega\) se obtienen oscilaciones libres subamortiguadas, amortiguamiento crítico y oscilaciones sobreamortiguadas.

2. Para un péndulo con fuerza de disipación proporcional a la velocidad calcule el trabajo que realiza la fuerza de rozamiento y compárelo con la pérdida de energía.

3. Verifique que si \(\Psi_1\) y \(\Psi_2\) son soluciones de la ecuación del oscilador armónico libre, cualquier combinación lineal \(\Psi = A_1 \Psi_1 + A_2 \Psi_2\) también es solución. Muestre que esto también vale si la fuerza disipativa es proporcional a la velocidad. ¿Vale si es un rozamiento constante?

4. Se tiene un péndulo que oscila con una disipación tal que su amplitud se reduce un 10% cada 10 oscilaciones. ¿Con que precisión deberíamos determinar su longitud para notar el corrimiento en su frecuencia debido al rozamiento?

5. Resuelva un oscilador armónico libre al que se le agrega una fuerza de rozamiento constante. Sugerencia: resuelva cada media oscilación agregando la fuerza que cambia la posición de equilibrio. Calcule el movimiento cada medio ciclo. Evalúe como cambia la amplitud cada medio ciclo. Calcule como es esa amplitud máxima en función del número de oscilación y compárela con una fuerza disipativa proporcional a la velocidad.

Oscilador armónico forzado

1. Considere un oscilador armónico en presencia de un rozamiento proporcional a la velocidad, sobre el que ahora se aplica también una fuerza dependiente del tiempo \(F(t) = F_{0}\cos(\Omega t)\).

   1. Suponga que t es suficientemente grande para que la solución transitoria haya decaído a cero (solución estacionaria). Proponga la solución particular \(x_{p}(t) = A\sin\left(\Omega t\right) + B\cos\left(\Omega t\right)\) y obtenga los valores de \(A\) y \(B\). Grafique cualitativamente \(A\) y \(B\) en función de \(\Omega\).

   2. Repita el ítem anterior pero ahora proponiendo como solución particular una función compleja \(x_{p}(t) = Ae^{i\Omega t}\). Para hacer esto, utilice la ecuación diferencial compleja con el forzado \(F(t) = F_0\,e^{i\Omega t}\) (¿porqué es lícito esto? ¿cómo recuperaría la solución particular real a partir de la solución particular compleja obtenida?).

   3. Grafique cualitativamente la posición de la masa en función del tiempo.

   4. Calcule la potencia media que se consume en el estado estacionario y la potencia media de pérdida por fricción. Verifique la igualdad de ambas potencias.

   5. Resuelva de manera completa el oscilador forzado excitado en el pico de resonancia (\(\omega = \omega_0\)) con la condición inicial de estar en reposo en su posición de equilibrio. Simplifique la expresión para el caso en que \(\gamma \ll \omega_0\) y grafíquela para poner en evidencia como el sistema tiende a su solución estacionaria.