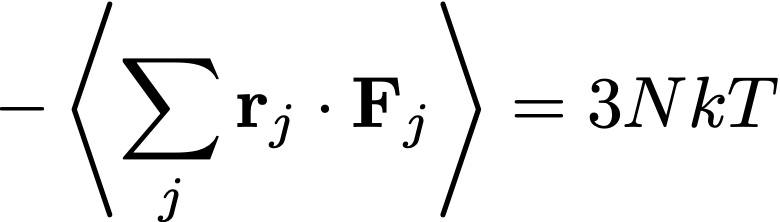Ya están disponibles en la página de la teórica el video de la clase de ayer y los apuntes para la clase de mañana. Y no dejen de ver el post con las excelentes noticias de la práctica.
En la clase de ayer vimos el teorema del virial. Este es un teorema muy útil, tanto en la versión de Mecánica Estadística como en su versión de Mecánica Clásica. Pero también es un teorema que puede ser fácilmente aplicado a situaciones en las que no se cumplen sus hipótesis, para obtener cualquier resultado (“No lo se Rick, parece falso”). Recuerden que las partículas en el sistema deben estar confinadas por el potencial. A continuación les doy dos ejemplos de aplicaciones (aunque no les voy a dar la fórmula para fabricar materia oscura condensada, y todos sabemos que no es dos partes de quarks plutónicos, una parte de cesio, y una botella de agua).
Comencemos con el gas ideal. Habíamos visto que el teorema del virial puede escribirse como
donde los r son las posiciones de las partículas, F son las fuerzas sobre cada partícula, N es el número de partículas, y T la temperatura. La suma es sobre todas las partículas. Para un gas ideal, la única fuerza que tenemos está asociada a la presión P. Usando que la fuerza total, sumada sobre todas las partículas, es ∑ r · F = – ∫ r · n P dA (donde n es la normal externa a la pared, y dA el diferencial de superficie), después de hacer algunas cuentas se puede llegar (usando el teorema de Gauss) a que el término de la izquierda es 3PV (con V el volúmen). ¡Por lo que recuperamos la ecuación de estado de un gas ideal: PV = NkT!
Veamos ahora una aplicación más oscura. Consideremos un clúster de N galaxias (es decir, una acumulación de galaxias en el universo), cada una con masa m y con masa total M = Nm. Las galaxias en el cluster están confinadas por la fuerza gravitatoria. Nos conviene ahora escribir el teorema del virial, para una fuerza que decae como el cuadrado de la distancia, como
donde U es la energía cinética y V ahora es la energía potencial. Asumiendo que el clúster es esférico, para la fuerza gravitatoria V = -3GM2/(5R), donde G es la constante de gravitación universal, y R el radio del clúster. Por otro lado la energía cinética media es <U> = M<v2>/2. De estas dos relaciones podemos estimar la masa del clúster como
La velocidad cuadrática media de las galaxias se puede medir, por ejemplo, por corrimiento Doppler. Y la masa del cluster se puede estimar de forma independiente a esta fórmula a partir de la luminosidad del cluster. Y aquí comienzan los problemas: esta fórmula da una masa M mayor que la que se estima con la luminosidad, sugiriendo que falta una fracción de materia no que no estamos observando. Este argumento puede ser ampliado para considerar otras formas de energía (por ejemplo, la energía en el campo magnético de las galaxias y el clúster), pero no cambia el resultado central. Este no es el único argumento a favor de la existencia de materia oscura, pero en conjunto con otros nos indica que cerca del 85% de la materia en el universo tiene que ser materia oscura.