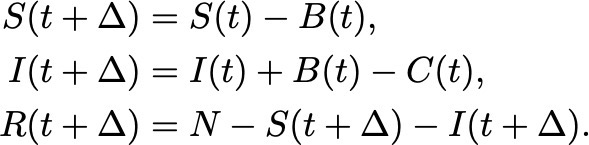Voy a contarles la historia de cómo John Snow aplicó la estadística en medicina, y cómo nos podría haber salvardo a todos del coronavirus. En 1854 John Snow salvó a Londres de un brote de cólera usando la estadística. ¿Pensaron que este posteo iba a ser sobre Jon Snow y Game of Thrones, o sobre el próximo House of the Dragon? ¿O sobre Elden Ring, guionado por el mismísimo G.R.R. Martin? Lo siento. Y va a ser aún mas aburrido, porque el Snow de esta historia no se revolcaba en la cama con aspirantes al trono de hierro. Pero el verdadero John Snow no solo salvó a Londres con la estadística, sino que por ese motivo es también considerado uno de los padres de la epidemiología moderna.
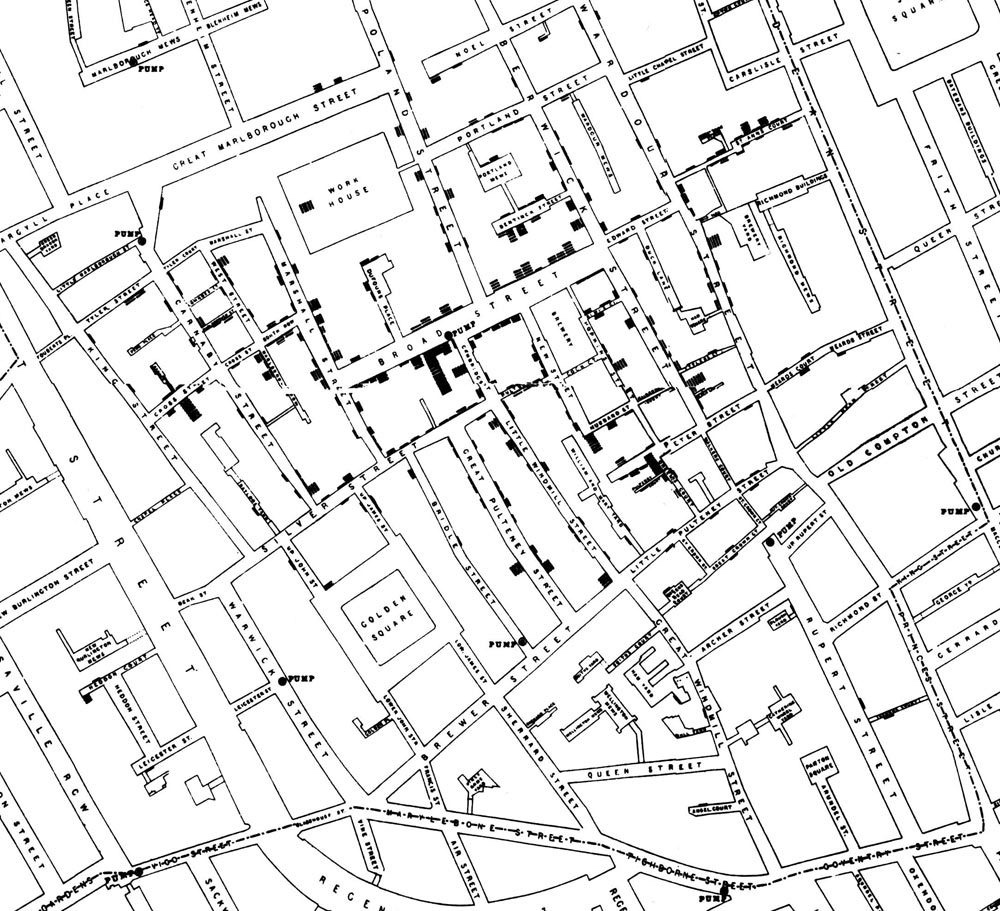
En esa época se pensaba que el cólera se transmitía por “miasmas” en el aire, que eran emitidos por material en descomposición y que enfermaban a quienes los respiraban. John Snow era médico en el Soho, y cuando se desató un brote de cólera desconfió de esta explicación. Sus vecinos y otros médicos lo acusaban de no saber nada (“You know nothing, John Snow”, ¡plop!), así que John Snow hizo el siguiente mapa con los casos de cólera que veía en el barrio:
Las barras negras son histogramas, y muestran el número de casos de cólera por casa (que están sospechosamente distribuidos en forma preferencial alrededor de un punto). Snow también hizo estudios “doble ciego” usando la información de que algunas casas usaban agua de una compañía y otras casas eran provistas con agua de otra empresa (y el número de enfermos en esas casas resultó ser diferente). Con estos datos, Snow concluyó que el cólera se debía contagiar por algún agente en el agua (Pasteur introduciría la idea de los gérmenes recién siete años después), e identificó a la posible fuente de agua contaminada como una bomba de agua en la esquina de Broad Street y Cambridge Street (que, efectivamente, había entrado en contacto con un pozo ciego). Los interesados pueden leer mas detalles sobre esta historia acá.
A fines prácticos, lo que nos importa es que John Snow realizó un experimento luego de identificar dicha bomba de agua para verificar su teoría: ordenó que remuevan la manija de la bomba, de forma tal que no se pudiera usar más. Y el número de casos de cólera disminuyó. Hoy en Londres, en el lugar donde se encontraba aquella bomba, está instalada una réplica (¡sin manija!) con una placa que recuerda los sucesos:
En el día de hoy la mecánica estadística se usa activamente para entender epidemias. Y también se usan modelos estocásticos similares al modelo de camino al azar que vimos en clase (aunque en el caso de epidemiología, suelen tener muchas más variables aleatorias). Los modelos más sencillos de epidemias tienen “compartimientos” (para individuos Susceptibles, Infectados y Recuperados, o SIR). Es decir, los números de individuos susceptibles (S), de individuos infectados (I) y de individuos recuperados (R) varían en cada paso (con el avance de los días) como variables aleatorias con alguna distribución de probabilidad conocida:
En estas ecuaciones, B(t) es una función de distribución (conocida) de la probabilidad de que un individuo susceptible se infecte en el tiempo t. Noten que cuando esto ocurre, el número de individuos susceptibles S disminuye, y el número de infectados I crece (t + Δ corresponde al tiempo luego de realizar un paso, por ejemplo, un día más tarde que el tiempo inicial t). De la misma forma, C(t) es una función de distribución, también conocida, de la probabilidad de que un individuo infectado se recupere. El número de individuos recuperados, R, se obtiene simplemente de pedir que la población total N no cambie en el tiempo. Noten cómo, a semejanza del modelo de camino al azar, contamos con algunas distribuciones de probabilidad conocidas (B y C, que describen propiedades de la enfermedad, equivalentes a la distribución de probabilidad f que vimos en clase), y el modelo nos permite calcular cantidades “macroscópicas” (la función de distribución de probabildad p): el número de infectados o de recuperados en una sociedad.
Partiendo de este modelo muy sencillo pueden construirse modelos más complejos (por ejemplo, con más “compartimientos” para considerar diferentes estadios de una enfermedad, para considerar poblaciones con diferentes edades, para considerar fallecimientos, o para considerar diferentes regiones de una ciudad o un país).
Este tipo de modelos, en el límite termodinámico tienden a ecuaciones diferenciales (más adelante también veremos cómo se obtiene el límite termodinámico de sistemas aleatorios) que describen cualitativamente la evolución de epidemias en poblaciones grandes. A lo largo del último año, en el medio de la epidemia de coronavirus, todo el mundo habló de estos modelos. Los que quieran saber más sobre modelos epidemiológicos pueden ver esta página, o leer este capítulo de un libro. El capítulo del libro tiene una discusión interesante sobre las limitaciones de los modelos, y sobre bajo qué condiciones se puede alcanzar la inmunidad de rebaño al introducir vacunas (esto no siempre ocurre). O pueden ver un trabajo que realicé con otros investigadores del Departamento de Física aplicado al caso particular de la transmisión de COVID-19 en la ciudad de Buenos Aires, o mirar un resumen de ese trabajo en este video.
Y los que se quedaron con ganas de Juego de Tronos, pueden seguir este link (aunque el link contiene lenguaje vulgar, y debido a su contenido, nadie debería verlo).