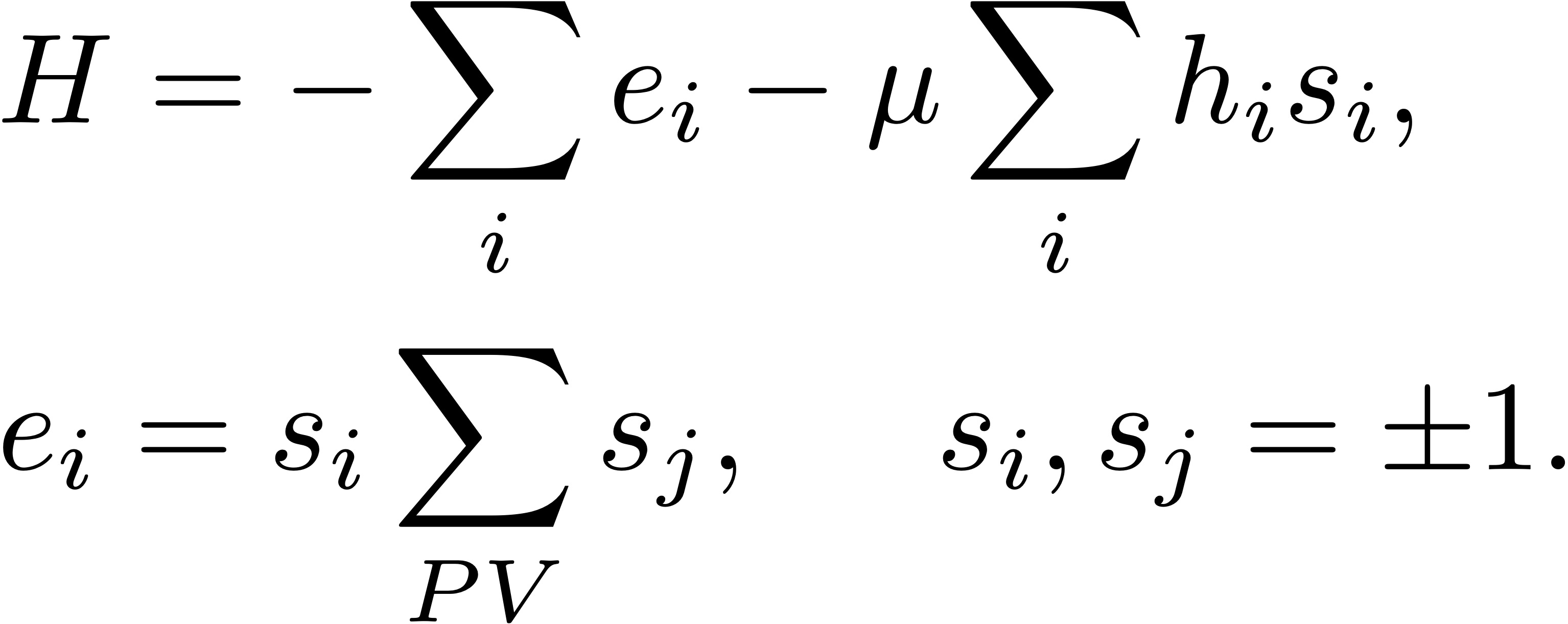Llegó el festival anual psicodélico de la criticalidad en la física y en áreas afines. Tenemos entradas para ver ejemplos de fenómenos críticos en física de materiales, sistemas biológicos, fluidos, cosmología, y hasta en neurociencias. Los links de bandas que tocaron en un festival de nombre similar llevan a videos en YouTube. ¡Y para escuchar más música está la playlist oficial de la materia! Y ahora sí, criticalidad y autosemejanza:

Comencemos con el lineup. En el escenario principal, después de Guns N’ Roses, tenemos dos ejemplos de física de materiales y materia condensada. Ya conocemos las transiciones de fase asociadas a los cambios de estado de la materia (sólido, líquido y gaseoso). ¡Pero existen muchos más cambios de fase! Así que veamos el show de bandas menos conocidas (y con ejemplos recientes de publicaciones en física). Primero tenemos a los cristales líquidos. Los cristales líquidos están formados por moleculas anisótropas (generalmente alargadas, por ejemplo con forma de largos cilindros), por lo que se comportan con propiedades intermedias entre los líquidos y los sólidos de acuerdo a en que dirección del material se aplican los esfuerzos. Y tienen al menos dos fases: en la fase nemática (a mayor temperatura) las moléculas están más desordenadas, pero se alinean a lo largo de sus ejes principales. En cambio, en la fase esméctica (a menor temperatura) las moléculas se acomodan en capas más ordenadas, y dentro de cada capa las moléculas están inclinadas con el mismo ángulo. El cambio entre ambas fases es una transición de fase con propiedades críticas. Los interesados pueden mirar un paper reciente (Gim, Beller & Yoon, Nat. Commun. 8, 15453, 2017), donde encontrarán esta figura alucinante con cambios morfológicos del material durante la transición (para temperatura creciente, de izquierda a derecha):

También pueden mirar este paper (el preprint de acceso libre está disponible acá) en el que los autores demuestran la existencia de una fase nemática en un modelo de cristales líquidos formados por barras en una red bidimensional. Y los que quieran leer otro ejemplo de transiciones de fase en materiales, pueden mirar este artículo sobre transiciones sólido-sólido que ocurren por cambios en la forma de partículas coloidales.

Vayamos a otro escenario del Criticalpalooza, y mientras escuchamos The Flaming Lips, veamos ejemplos recientes de transiciones de fase y autosemejanza observados en sistemas biológicos. Ciertas células cambian sus patrones de movimiento de acuerdo a la densidad de células en su entorno. A baja densidad muestran un movimiento desordenado, mientras que a alta densidad muestran patrones de movimiento colectivo y ordenado. La transición entre ambos comportamientos ocurre como una transición de fase. Pueden ver un ejemplo en Szabó et al., Phys. Rev. E 74, 061908 (2006) (el preprint está diponible en este link). La siguiente figura, de ese paper, muestra los patrones de movilidad al aumental la densidad de las células (de izquierda a derecha). Noten el cambio en el orden del sistema:

Los que tengan interés por ver más aplicaciones en biofísica, pueden mirar también un paper sobre fenómenos críticos en membranas lípidas (¡donde estiman exponentes críticos!).

En el mismo escenario donde toca Metallica tenemos una variedad de fenómenos autosemejantes que se observan en fluidos. El más conocido es el fenómeno de la turbulencia, que es heavy metal. Los fluidos más viscosos (donde la viscosidad se mide con un número adimensional, el número de Reynolds) fluyen en forma ordenada y laminar. Pero al aumentar el número de Reynolds (y reducirse la importancia de la viscosidad), generan flujos muy desordenados que tienen propiedades de invariancia de escala. En la siguiente figura, noten como zooms sucesivos en el flujo parecen repetir los patrones (algo similar a lo que vimos en el modelo de Ising en 2D):

Esta es una transición extraña, porque los flujos turbulentos tienen propiedades de criticalidad y autosemejanza, pero son un sistema fuera del equilibrio. Pueden ver más imágenes de flujos turbulentos aquí. Y pueden ver un ejemplo de una transición de fase en turbulencia en un condensado de Bose-Einstein en este paper.

Los que tengan interés por cosmología pueden ir al escenario donde tocan Empire of the Sun y Lee Smolin, y leer este artículo donde se discuten diversos problemas (como la formación de galaxias espirales, la estructura de gran escala del universo, o el universo temprano) desde el punto de vista de fenómenos críticos. Bastante más difícil de leer, pero que sirve como ilustración, es este paper donde se estudia una transición de fase al compactificar una dimensión en teorías de gravedad (compactificar es “enrollar” una dimensión sobre si misma, y hacer tender ese “rollo” a cero). Y en cosmología, algunas teorías predicen que otra transición de fase podría haber ocurrido en el universo temprano, cuando se formaron los primeros átomos. Luego de ese momento el universo se volvió transparente, pero antes de ese instante el universo puede haber sido opalescente en forma crítica (como la mezcla de un líquido y un gas cuando llega a la temperatura crítica y dejan de existir las diferencias entre ambas fases, como se ve en la foto del centro en esta imágen de una mezcla de etano líquido y gaseoso tomada de Wikipedia):

Ya que estamos en el festival, no nos olvidemos de ir a ver las bandas clásicas. El mecanismo de Higgs por el cual los bosones de gauge adquieren masa, es también un mecanismo de ruptura espontánea de la simetría.

Para cerrar el festival, este Criticalpalooza no tendrá a The Strokes, pero tiene ejemplos de fenómenos críticos en el cerebro (¿lo entendieron?). Las funciones cognitivas involucran procesos que van desde las neuronas individuales hasta regiones grandes del cerebro, y en los últimos años se encontró evidencia creciente de que el cerebro funciona en el borde entre el orden y el desorden, con propiedades de fenómenos críticos. Los interesados en ver ejemplos de criticalidad y autosemejanza en el cerebro pueden mirar este paper o este paper. La siguiente imagen, tomada de Cochi et al., Progress in Neurobiology 158, 132 (2017) (el primero de los dos papers) es bastante sugerente:

¿Matan las pulgas a sus pulgas con matapulgas? Y ¿sueñan los androides con ovejas eléctricas? Tanto el título de la novela de Philip K. Dick (que inspiró a la película Blade Runner), como un famoso poema de Jonathan Swift, exploran la idea de la repetición en diferentes grados o escalas. En la novela de Philip Dick los humanos crean a los androides, y los androides sueñan como los humanos pero con ovejas eléctricas. En el poema de Swift, las pulgas tiene pulgas más pequeñas que se alimentan de ellas, que a su vez también tienen sus pulgas:

So, naturalists observe, a flea
has smaller fleas that on him prey;
and these have smaller still to bite ‘em,
and so proceed ad infinitum.
Jonathan Swift, On poetry: A rhapsody (1733).

Maurits Escher exploró una idea similar en su xilografía Más y más pequeño (1956), en la que un patrón de reptiles se repite hasta alcanzar tamaños infinitamente pequeños y números infinitamente grandes:

Sorprendentemente, en ausencia de campo magnético externo y cerca de la temperatura crítica (T_c) en la cual se pierde la magnetización permanente, el modelo de Ising en dos dimensiones presenta estructuras similares, que se repiten en diferentes escalas. En las próximas clases comenzaremos a estudiar este comportamiento en forma teórica y usando simulaciones (también pueden explorarlo mientras hacen la práctica computacional). Pero comencemos por ver un video que muestra un barrido del sistema en función de la temperatura, en el entorno cercano a la temperatura crítica:

La barra de colores de la derecha muestra la temperatura (normalizada por la temperatura crítica). Al principio del video (T > T_c) el sistema no tiene magnetización permanente. En la mitad del video (T ≈ T_c, cerca del minuto 0:50) se observan islas magnéticas de tamaños muy diferentes y con bordes rugosos. Y finalmente, hacia el final del video (T < T_c) se observan islas muy grandes, con el tamaño característico del dominio, y con bordes más suaves.

Cerca de la temperatura crítica, la presencia de islas de diferentes tamaños vuelve al sistema invariante de escala, como las pulgas del poema de Jonathan Swift, o como los reptiles en la xilografía de Maurits Escher (aunque en el caso del modelo de Ising, los patrones están más desordenados). Esto está muy bien ilustrado en el siguiente video, que muestra un estado del modelo de Ising con 1,7×10¹⁰ nodos, cerca de T_c. Al principio el video muestra lo que parecen ser cuatro realizaciones independientes del modelo de Ising, pero en realidad son partes más chicas de la simulación completa:

Ex Machina es una película de 2014 con algunos giros de tuerca inquietantes alrededor de la idea de construir máquinas con inteligencia artificial. Y, sorprendentemente, los temas de esta materia tienen una relación cercana con este problema. El premio Nobel de Física 2021 fue otorgado a Giorgio Parisi, Syukuro Manabe y Klaus Hasselmann por contribuciones fundamentales a la comprensión de los sistemas complejos. Y en particular, la mitad del premio Nobel fue para Giorgio Parisi, entre otras cosas, por sus aportes al estudio de los vidrios de spin. Los vidrios de spin son un modelo sencillo para sistemas magnéticos amorfos, un caso en cierto sentido más general que el de los modelos de Ising que estamos considerando en el curso.

Ustedes podrán preguntarse qué relación hay entre vidrios de spin e inteligencia artificial. Comencemos por un problema más sencillo (o tal vez mucho más difícil): el juego de Go. El Go es un juego de mesa, pariente del ajedrez, en el que dos jugadores ponen piedras blancas o negras en turnos, en cualquier lugar del tablero, en una cuadrícula de 19×19 puntos. El objetivo del juego es rodear la mayor cantidad de territorio posible con las piedras del color del jugador.

Las reglas son muy sencillas: (1) Una piedra sin libertades (es decir, completamente rodeada por piedras del color opuesto) es capturada y removida del tablero. (2) No se pueden hacer jugadas que recreen la situación previa del tablero. Y (3) cuando un jugador pasa su turno dos veces seguidas, el juego termina. A pesar de esta simpleza (o tal vez como resultado de la misma), es un juego muy complejo. El número de posiciones legales en el tablero es mayor a 10¹⁷⁰ , muchísimo más grande que en el ajedrez, y más grande que el número de átomos en el universo. Como resultado, los métodos para hacer que computadoras jueguen al Go calculando todas las jugadas posibles (como se hace con el juego de ajedrez) son inviables. Así, el juego de Go resulta un desafío más que interesante para la inteligencia artificial.

Hasta hace unos años, uno de los métodos preferidos para programar computadoras para jugar al Go era aplicar el método de Montecarlo para encontrar configuraciones del tablero que minimicen la energía (o el Hamiltoniano) de un modelo de Ising que tuviera alguna relación con las reglas del juego de Go y con las condiciones para ganar una partida. Por ejemplo, un posible Hamiltoniano es el siguiente, donde s_i es el color de las piedras en cada posición (+1 o -1 para blanco o negro), h_i es el número de libertades de la piedra i-ésima (cuantos casilleros tiene libre alrededor), PV indica que la suma se hace sobre los primeros vecinos, y μ (>0) es una “energía” que premia las configuraciones en las que las piedras propias (+1) tienen libertades (es decir, no están rodeadas):

¡De pronto, el modelo de Ising y el método de Montecarlo encuentran aplicaciones muy lejos de la física de materiales magnéticos! Sin embargo, estos métodos resultan en programas de Go que juegan apenas tan bien como un jugador humano mediocre. Y cuando el problema de jugar bien al Go parecía inaccesible para las computadoras, Google presentó en 2016 una red neuronal profunda que le ganó a todos los grandes campeones humanos del juego.

Una red neuronal profunda es una red con muchas capas de neuronas artificiales: los datos ingresan (en la siguiente figura, por la izquierda), son multiplicados por coeficientes (llamados “pesos”) en cada conexión entre neuronas, y el resultado es procesado con alguna operación sencilla por cada neurona (que puede estar “activada” o “inactivada”). El procedimiento se repite en cada capa de neuronas, hasta que se obtiene un resultado final (por dar un ejemplo muy crudo y simplificado, ingresa el estado actual del tablero de Go y obtenemos como resultado la próxima jugada que conviene realizar):

Las redes neuronales son entrenadas con muchísimas jugadas, de forma tal de ajustar los pesos en cada una de las conexiones de las neuronas y obtener un resultado óptimo. Pero noten que la estructura de la red no es muy diferente a la de los sistemas magnéticos que estuvimos estudiando en el curso: tenemos nodos que interactúan con sus vecinos con algún coeficiente de acoplamiento, y su equilibrio corresponde al mínimo de alguna función (el error en la respuesta que obtenemos). La diferencia es que ahora esos coeficientes (los pesos) no están fijos, y pueden cambiar durante el entrenamiento.

En física ocurre algo similar en materiales magnéticos amorfos. La estructura de la red de spines en esos materiales puede ser muy compleja, y los spines pueden interactuar con otros spines muy lejanos (en la peor situación posible, pueden interactuar todos contra todos). Y los spines pueden tener coeficientes de acoplamiento diferentes para cada par, que en la siguiente figura se indican como J_ij para el acomplamiento del par (i,j). La variante de los modelos de Ising que se usa para estudiar este tipo de sistemas es conocida como vidrios de spin:

Los vidrios de spin son formalmente equivalentes a un tipo particular de redes neuronales (llamadas redes de Hopfield), pero muchos de los resultados que se obtuvieron para vidrios de spin se trasladan a la teoría de redes neuronales en forma muy general. Al construir la mecánica estadística de estos sistemas, la dificultad radica en que no solo es necesario armar ensambles con copias de todos los alineamientos posibles de los spines, sino que también es necesario armar réplicas del sistema con diferentes acoplamientos J_ij (ya que uno no sabe cuánto valdrán los pesos, o los acoplamientos). Parisi hizo contribuciones muy relevantes que permitieron atacar este problema, y entender propiedades generales de los estados de equilibrio.

Los vidrios de spin, dada su complejidad, no tienen un único equilibrio: tienen una variedad muy grande de equilibrios posibles, que corresponden a mínimos locales de su energía libre. Así, la mecánica estadística de los vidrios de spin también nos da información sobre a qué estados posibles puede decaer una red neuronal durante el proceso de aprendizaje, o nos permite saber que ciertas redes neuronales pueden guardar “recuerdos”, y calcular la máxima cantidad de información que puede almacenarse en esas redes en función de su estructura, del número de neuronas, y del número de conexiones entre las neuronas.

Los que quieran saber más sobre el premio Nobel de Física 2021 (que también tiene aplicaciones en el estudio del cambio climático) pueden ver este coloquio que di en el DF con Gabriel Mindlin.

“Now I am become Death,
the destroyer of worlds.”
Robert Oppenheimer (1904-1967).

La mecánica estadística, que nació a fines del siglo XIX y principios del siglo XX a partir de los trabajos de Boltzmann, Maxwell y Gibbs, tuvo un rol importante durante la Segunda Guerra Mundial. El proyecto Manhattan, que entre 1939 y 1946 reunió a varios de los científicos más brillantes de la época, usó frecuentemente sus herramientas e impulsó el desarrollo de métodos que ampliaron enormemente su área de aplicación. Los científicos que participaron del proyecto entendían lo que estaban haciendo. Albert Einstein y Leo Szilard instaron a Roosevelt, el presidente de los Estados Unidos, a construir una bomba atómica frente a la amenaza de que los alemanes la construyeran antes. Comprendían las consecuencias y más tarde sintieron remordimiento por los muertos que la bomba causó, o firmaron manifiestos alertando sobre los riesgos de la carrera armamentista. Pero aunque a veces la bondad o la maldad pueden relativizarse, en ciertas ocasiones las personas se encuentran frente a la maldad en estado puro, absoluta. Y frente a eso hasta el famoso pacifismo de Einstein pudo aceptar un hiato.

En las últimas clases comenzaron a aparecer métodos, y diversos nombres de científicos, que estuvieron relacionados con el proyecto Manhattan. Así que vamos a dedicar este posteo a algunos de ellos. El proyecto Manhattan tuvo como objetivo fabricar armas nucleares para los Estados Unidos durante la guerra. Jugó un rol central en el fin de la guerra del Pacífico, mostró lo que puede hacer la colaboración científica a gran escala, y generó desarrollos rápidos e importantes. Pero, como ya mencioné, aún hoy se sigue discutiendo la necesidad de bombardear Hiroshima y Nagasaki, o la carrera armamentista nuclear que siguió a continuación. Sobre esa época, y para reflexionar sobe esos temas, les aconsejo “Dr. Strangelove, or How I Learned to Stop Worrying and Love the Bomb” (1964), una película satírica de Stanley Kubrick que es un clásico del cine, y en la que el genial Peter Sellers tiene tres papeles (el presidente de los Estados Unidos, un capitán británico, y el científico nazi Dr. Strangelove).

En particular, en la última clase vimos el método de campo medio para el problema de Ising desarrollado por Hans Bethe. Bethe publicó este resultado en 1935, el año en que se mudó a los Estados Unidos (pueden ver el paper original aquí). Bethe trabajó en el proyecto Manhattan y luego en el desarrollo de la bomba de hidrógeno junto con Edward Teller y Stanislaw Ulam (yo tuve la suerte de conocer y hablar varias veces con Stirling Colgate, que trabajó con Teller y Bethe en ese proyecto; probablemente el apellido les resulte conocido de algún lado). Luego Bethe trabajó en la formación de elementos químicos por fusión nuclear en el interior de las estrellas, por el que ganó el premio Nobel en 1967. La mecánica estadística jugó roles importantes en estos trabajos. Pero su paper más famoso es un paper en el que no trabajó. En 1948, luego de la guerra, Ralph Alpher y George Gamow escribieron un trabajo sobre la formación de los primeros átomos en el universo. Gamow, al enterarse que el paper iba a salir publicado el 1 de abril (“April fools’ day“, el equivalente a nuestro día de los inocentes), agregó a Hans Bethe como segundo autor. Así, el paper de Alpher, Bethe y Gamow se volvió conocido como el paper α-β-γ (alfa, beta y gama). Más tarde, cuando Ralph Alpher trabajó con Robert Herman en el cálculo de la temperatura de la radiación cósmica de fondo, Gamow quiso convencer a Herman de que cambiara su apellido por “Delter”, para poder escribir un paper con autores Alpher, Bethe, Gamow y Delter (α-β-γ-δ). Herman se negó rotundamente.

El método de Montecarlo que se usa para resolver numéricamente el modelo de Ising también fue creado durante el proyecto Manhattan. Muchas veces se dice que Stanislaw Ulam inventó al método tal como lo conocemos hoy mientras trabajaba en el proyecto de la bomba atómica. Sin embargo, el método fue el resultado del trabajo conjunto de varias personas, que formaban parte de un grupo liderado por Nicholas Metropolis, y entre las que se encontraban Ulam, John von Neumann, Edward Teller, Augusta H. Teller, Marshall Rosenbluth y Arianna W. Rosenbluth. Casualmente los Teller (Edward y Augusta) se mudaron de su Hungría natal a Estados Unidos en 1935, antes de la segunda guerra mundial, por invitación de George Gamow (el del paper α-β-γ), mostrando como todo se conecta con todo.

Es muy probable que la idea original para el método de Montecarlo haya nacido de von Neumann y Ulam. Y que los Teller y los Rosenbluth (dos parejas de físicos) hicieran el grueso del trabajo, desarrollado las ideas e implementando el código numérico para poder probarlo en MANIAC I, una de las primeras computadoras de Los Alamos. En particular, hoy sabemos que el trabajo de Augusta Teller y de Arianna Rosenbluth fue central, aunque en aquella época no fue tan valorado. Augusta Teller escribió la primera versión del programa de Montecarlo para MANIAC I, mientras que Arianna Rosenbluth fue la encargada de escribir el programa definitivo (¡en código de máquina!) que fue usado para calcular, usando mecánica estadística, la difusión de neutrones en el material para la fisión nuclear, y más tarde (luego de terminada la guerra) para calcular los resultados sobre el algoritmo que se reportaron en los papers. Lamentablemente los prejuicios de la época, y el hecho de que ambas dejaran de ejercer su profesión para dedicarse a sus familias, hicieron que no recibieran el crédito merecido y que quedasen pocos documentos y fotos de ellas:

Luego de la guerra, Metropolis y Ulam publicaron el primer paper no clasificado explicando el método en detalle. Y más tarde Metropolis, Marshall y Arianna Rosenbluth, y Edward y Augusta Teller publicaron otro paper, famoso y que usualmente se considera la referencia para el algoritmo. Hoy el método de Montecarlo se usa para resolver en forma numérica una gran variedad de problemas en física y en ciencia de datos, y es central en el modelado de problemas de mecánica estadística.

Los que quieran leer más sobre Arianna W. Rosenbluth, y sobre el desarrollo del método de Montecarlo, pueden mirar estos links:

• El obituario de Arianna Rosenbluth en The New York Times: tiene muchos detalles interesantes sobre su carrera, incluyendo el hecho de que Felix Bloch se negó a tomarla como estudiante doctoral porque él no trabajaba con estudiantes mujeres.
• Un paper en Physics of Plasmas sobre la creación del método de Montecarlo tal como lo contó Marshall Rosenbluth en un congreso, en el que también destaca el rol de Arianna. El paper tiene una breve (pero clara) descripción del método.

Los que quieran leer más historias sobre el proyecto Manhattan pueden mirar también las memorias de Richard Feynman (¡este texto está muy recomendado, incluye lecciones sobre cómo abrir cajas fuertes!):

• Los Alamos from below

El modelo de Ising es un modelo de juguete para el ferromagnetismo. Sin embargo, esto no significa que sea un modelo poco importante, o que solo tenga utilidad pedagógica. En cierto sentido, el modelo de Ising es el Buzz Lightyear de los modelos de juguete. El modelo, en su forma más sencilla y en dos dimensiones, consiste en un arreglo de espines (o dipolos magnéticos) que solo pueden tomar dos valores (+1 o -1). En ausencia de un campo magnético externo, los dipolos interactúan entre sí tratando de alinearse con sus vecinos más cercanos. A bajas temperaturas este arreglo de espines tiende a generar islas con la misma orientación, y si tenemos más espines con un signo que con el otro, entonces el material estará magnetizado. La transición entre el material no magnetizado y el material magnetizado, al bajar la temperatura, es una transición de fase similar (aunque no del mismo orden) a los cambios en los estados de agregación de la materia.

El desarrollo de la mecánica estadística entre fines del siglo XIX y principios del siglo XX, de la mano de Boltzmann y de Gibbs, permitió a los físicos comprender mejor varios sistemas y procesos (como el gas ideal, o los fenómenos de transporte), formalizar conceptos (como la noción de equilibrio, los microestados, el desorden, y la entropía), y estudiar fenómenos nuevos (como el condensado de Bose-Eistein, o la superfluidez y la superconductividad). Además, la mecánica estadística amplió el campo de aplicación de la física a otras áreas y a temas interdisciplinarios, como vimos en este post.

Sin embargo, aún en 1944 (más de 70 años después de la publicación de la ecuación de Boltzmann) no estaba claro si la mecánica estadística podría capturar y ayudar a comprender las transiciones de fase, como ocurren en la transición de agua líquida a vapor de agua, o en la magnetización espontánea de ciertos materiales (reales, no de juguete) al bajar su temperatura. Y aquí es donde el modelo de Ising, y Lars Onsager, abrieron las puertas a muchos desarrollos cruciales para la física en la segunda mitad del siglo XX. En 1944 Onsager encontró una solución exacta al modelo de Ising en dos dimensiones, calculando la función de partición del sistema, mostrando que podía sufrir una transición de fase y magnetizarse espontáneamente, y calculando la temperatura a la que ocurre la transición. La solución mostró por primera vez que las transiciones de fase aparecen como singularidades de las funciones termodinámicas del sistema, y convenció a los físicos de que la mecánica estadística podía ser usada para estudiar estos fenómenos. Fue tan relevante que al terminar la segunda guerra mundial, cuando varios físicos volvieron a la investigación básica, Hendrik Casimir le comentó en una carta a Wolfgang Pauli que estaba preocupado y dudaba de si podría volver a trabajar en física teórica luego de haber perdido contacto con el tema por tanto tiempo. Pauli (que era famoso por evaluar las teorías de sus colegas muy duramente) lo tranquilizó respondiendo que durante la guerra solo hubo un resultado que debía mirar: “No ha ocurrido mucho que sea de interés, excepto por la solución exacta de Onsager al modelo de Ising en dos dimensiones“.

Onsager es un personaje interesante. Muchos de sus resultados no fueron publicados en papers. La solución exacta al modelo de Ising apreció como una discusión de otro paper, su formula para la temperatura de la transición quedó en un pizarrón luego de un seminario que dió László Tisza, y la predicción de la cuantización de vórtices en un superfluido (luego redescubierta por Feynman) apareció en una paper resumiendo un seminario de otro investigador, en la sección de preguntas y respuestas del público.

Los que quieran jugar un poco con el modelo de Ising en 2D (antes de la práctica numérica), pueden mirar la siguiente página donde pueden simular el sistema con el método de Montecarlo, y variar la temperatura y el campo magnético externo. Para un campo externo igual a cero, prueben ver que pasa con la amplitud de las fluctuaciones en la magnetización si se acercan a la temperatura crítica (T_c ≈ 2.27) desde arriba (es decir, desde temperaturas altas):

• Modelo de Ising en 2D

Para terminar, no se pierdan el video en el que Onsager le explica a Ising que solo es un juguete:

“¡Todos pueden ser súper! ¡Y cuando todos sean súper, nadie lo será!” La película Los increíbles (2004) tiene a uno de los villanos más interesantes de las películas de superhéroes. Syndrome no busca dominar al mundo, no desea poder o dinero. Desea que todos sean iguales, y que los superhéroes dejen de ser especiales. ¿Eso es algo bueno, no? ¿Por qué Syndrome sería entonces un villano? Sin embargo, al ver la película, algo parece incorrecto (y casi perverso) en pedirle a Dash con sus 10 años que no participe en el equipo de atletismo de su escuela porque sería excepcional. La película, que a primera vista parece un simple pasatiempo, plantea una discusión interesante sobre la excepcionalidad, la igualdad, y el festejo de la mediocridad.

Los superfluidos son excepcionales. Y algunas de las cosas que hacen son realmente increíbles. Un superfluido es un fluido que fluye sin viscosidad, lo que les permite atravesar canales muy delgados o medios porosos (por los que un fluido viscoso no podría pasar), o trepar por las paredes del recipiente que los contiene. El fenómeno de superfluidez se debe a la formación, a temperaturas muy bajas, de un condensado de Bose-Einstein en el que una fracción de los átomos que formal el fluido (usualmente Helio-4) dejan de tener agitación térmica (sin embargo, la teoría de condensados que vimos en clase corresponde a gases débilmente interactuantes, mientras que el Helio-4 superfluido es un líquido, con una energía potencial de interacción entre sus átomos que no es despreciable). El fenómeno está relacionado también con el de superconductividad.

El siguiente video, muy corto (1:44 minutos) pero muy recomendable, muestra varias de las propiedades más llamativas de los superfluidos, como la capacidad de trepar por las paredes de un recipiente, o el “efecto fuente”:

Luego pueden ver un video mas reciente (en castellano) con experimentos de vórtices cuantizados en He-4 superfluido. Como vimos en clase, el hecho de que los bosones que forman el superfluido sean indistinguibles, hacen que los vórtices en el flujo no puedan rotar a cualquier velocidad, y que su circulación se cuantice. Las lineas blancas sobre fondo negro que se ven en los primeros 5 segundos del video son vórtices cuantizados observados en el laboratorio:

Para los que quieran leer mas sobre He-4 superfluido, les aconsejo leer el siguiente trabajo de Richard Feynman. Aunque es un poco antiguo y la interpretación actual de los rotones es diferente a la planteada en el artículo, muchas de las especulaciones que hace Feynman fueron mas tarde confirmadas en experimentos:

• Application of quantum mechanics to liquid Helium

Este trabajo tiene una historia interesante atrás. Feynman presentó, antes de escribir el artículo, sus resultados en un congreso al que asistió Lars Onsager (que era famoso en el área). Feynman estaba bastante orgulloso de si mismo (por estos resultados, pero también se encontraba en ese estado la mayor parte del tiempo), y Onsager decidió darle una lección. La narración completa la pueden encontrar en “Surely You’re Joking, Mr. Feynman!“, pero en palabras de Feynman es más o menos así:

“Bueno, Feynman”, dijo Onsager con voz ronca, “escuché que crees que has entendido el helio líquido”.
“Bueno, sí…”
“Umm…” ¡Y eso fue todo lo que me dijo durante toda la cena! No fue muy estimulante.

Al día siguiente di mi charla, y expliqué todo sobre el helio líquido. Al final, mencioné que había algo que todavía no había logrado entender: si la transición entre una fase y la otra del helio líquido era de primer orden (como cuando un sólido se derrite o un líquido hierve, y la temperatura se mantiene constante) o de segundo orden (como ocurre en el magnetismo, donde la temperatura puede cambiar).

Entonces el profesor Onsager se levantó y dijo duramente: “Bueno, el profesor Feynman es nuevo en nuestra área, y creo que necesita ser educado. Hay algo que tiene que aprender y que debemos decirle”.
Pensé: “¡Oh no! ¿Qué hice mal?”
Onsager dijo: “Deberíamos decirle a Feynman que nadie ha podido obtener el orden de una transición a partir de primeros principios, por lo que el hecho de que su teoría no le permita calcular eso no significa que no haya entendido todo los otros aspectos del helio líquido satisfactoriamente”. Resultó ser un cumplido, pero por la forma en que comenzó, ¡pensé que me iba a dar una paliza!

Aunque Onsager probablemente nos daría una paliza, en nuestro grupo de investigación trabajamos (entre otros temas) en el estudio de flujos y turbulencia en superfluidos y en condensados de Bose-Einstein. En los dos primeros links pueden ver algunas imágenes y videos de simulaciones que hicimos de vórtices cuantizados. Para los mas curiosos (o valientes), en el tercer link les dejo un paper que publicamos hace unos años sobre viscosidad en superfluidos a temperatura finita; el paper usa muchas herramientas de la materia como el ensamble gran-canónico, el potencial químico, fonones y relaciones de dispersión, y teoría cinética y camino libre medio:

• Imágenes de simulaciones de turbulencia cuántica
• Videos de nudos de vórtices cuantizados
• Paper: Quantitative estimation of effective viscosity in quantum turbulence
• Finalmente, la página de nuestro grupo de investigación con más información

En la película Spectral (no recomendada por esta materia), unos condensados de Bose-Einstein toman vida y congelan a las personas hasta la muerte. Por suerte, gracias al poder de la ciencia, pueden ser atrapados por materiales cerámicos y por el hierro, y por una pistola de pulsos que destruye al condensado (Yeah, science!). En el laboratorio hay pocas chances de que un condensado de Bose-Einstein cobre vida (pero por las dudas, no se acerquen al Laboratorio de Iones y Átomos Fríos del DF). Así que en este post vamos a ver qué es y cómo se ve un condensado en la realidad.

¿Qué es un condensado de Bose-Einstein? Comencemos por recordar que en la naturaleza toda la materia que conocemos se separa en dos tipos: fermiónica y bosónica. Los fermiones (como los electrones) satisfacen el principio de exclusión de Pauli: no podemos encontrar dos electrones en el mismo estado. Todos quieren ser diferentes. Los bosones (como los átomos de helio) tienen el comportamiento social contrario: no les molesta ser todos iguales, y estar todos juntos. Los fermiones escuchan jazz, los bosones son rolingas. Entonces, un gas de bosones (como los átomos de helio), muy frío, no se comporta como un gas clásico (es decir, como un montón de partículas separadas). Se comporta como si fuera una única partícula cuántica muy gorda, que puede tener tamaños que podemos observar a simple vista, pero que está descripta por una única función de onda. La noción de “átomos” como pelotitas independientes se borra. Y se borra en escalas macroscópicas: tenemos una bola de gas que actúa como un único objeto cuántico.

A continuación les dejo algunos videos sobre condensados de Bose-Einstein. Como los videos son largos, para aquellos que tienen síndrome de déficit de atención les digo también a qué instante pueden saltear para ver algunas cosas interesantes. Como mencioné en la clase de hoy, recién en 1995 se realizaron los primeros experimentos de condensados de Bose-Einstein en gases diluídos de átomos ultrafríos, en los que la interacción entre los átomos es débil:

El video muestra un experimento con un gas de átomos de sodio. La descripción del experimento ocurre entre el minuto 0:46 hasta 2:50. A partir del minuto 3:10 hasta 3:50 pueden ver mediciones de la temperatura en el gas, y la formación del condensado de Bose-Einstein.

Los que tengan un poco mas de paciencia pueden ver la charla completa de Eric Cornell cuando recibió, junto con Carl Wieman y Wolfgang Ketterle, el premio Nobel por conseguir el primer condensado de Bose-Einstein gaseoso en el laboratorio:

• Nobel Lecture by Eric A. Cornell

El video dura 39 minutos. Los que quieran pueden saltear la introducción e ir al minuto 5:23 hasta 7:03, donde Cornell explica el rol que juega la longitud de onda de de Broglie en la transición de fase (algo que vimos en la última clase). A partir del minuto 28:49, Cornell muestra imagenes de vórtices cuantizados en el condensado, un tema que veremos en la próxima clase. Entre otras cosas, en el próximo post pondré videos de superfluidos escapándose espontáneamente de sus recipientes (¡seguro hay una película de ciencia ficción que se aprovecha de este fenómeno!).

Pero antes de despedirnos, recuerden que el espacio es la frontera final. Hace unos pocos años la NASA consiguió generar un condensado de Bose-Einstein en el espacio (más precisamente, en la estación espacial internacional).

¿Para qué hicieron esto? Para poder realizar mediciones, en los experimentos se debe “soltar” al condensado: se apaga el potencial armónico que lo mantiene atrapado, y se deja que el gas se expanda libremente. En la Tierra, la gravedad hace que al liberar el condensado llegue un instante en el que esa nube de gas degenerado se separe en sus átomos originales, diferentes y con sus propias funciones de onda (es decir, los rolingas recuperan sus personalidades individuales, y luego del recital, vuelven a sus trabajos de oficina). La gravedad también pone un límite a cuán grande puede ser el condensado original, porque la gravedad hace eso: intenta tirar a las partículas para abajo. Como dice la canción de Charly García, la gravedad “te tira para atrás, te pide más y más, y llega a un punto en que no querés“. En este caso, el que no quiere más es el condensado. Pero sin gravedad (o en realidad, en la constante caída libre de la estación espacial internacional), se pueden armar condensados de Bose-Einstein más grandes, y medir por más tiempo mientras el gas se expande, manteniendo la bola de rolingas impersonales. En ausencia de gravedad, el salto del pogo dura más tiempo.