¿Qué puede ser más sencillo que la física de una bolsa arrastrada por el viento? ¿O de un grano de polen sumergido en agua en reposo? Como aprendieron Robert Brown, Albert Einstein y Marian Smoluchowski a mediados del siglo XIX y principios del siglo XX, a veces hay tanta belleza en el mundo que no puede explicarse en forma sencilla.
La física de partículas sumergidas en fluidos, aunque en una primera impresión puede parecer sencilla, ha jugado un papel central en el desarrollo de la mecánica estadística y en nuestra comprensión actual de sistemas en equilibrio termodinámico (y también de sistemas que están fuera de equilibrio). El movimiento browniano fue descrito por primera vez por Robert Brown en 1827, mientras observaba un grano de polen sumergido en agua en el microscopio. Brown notó que el grano de polen parecía moverse y sacudirse al azar, sin ninguna razón aparente.
A principios del siglo XX, Einstein y Smoluchowski explicaron este fenómeno asumiendo que el choque de las moléculas de agua con el grano de polen producían el movimiento de la partícula observado en el microscopio. Esto permitió verificar en forma indirecta la existencia de átomos y moléculas en experimentos. Pero el movimiento browniano, y las teorías de Einstein y Smoluchowski, marcaron también el camino para el estudio de procesos de difusión y de los procesos aleatorios. Y las partículas sumergidas en fluidos siguen dando sorpresas aún hoy. Muy recientemente, experimentos usaron partículas coloidales sumergidas en líquidos para verificar una relación para las fluctuaciones en sistemas fuera del equilibrio termodinámico conocida como la igualdad de Jarzynski (una igualdad que nos dice que en sistemas fuera del equilibrio la entropía puede disminuir, pero que la probabilidad de que esto ocurra es mucho menor que la probabilidad de que la entropía aumente; más adelante vamos a volver sobre este tema en otro posteo). Y un sistema similar se usó para verificar una predicción de Landauer de 1961, que dice que borrar información tiene un costo termodinámico: cada vez que se borra información debe realizarse una cantidad mínima de trabajo, aumentando inevitablemente la entropía del sistema (otro tema sobre el que volveremos más adelante).
En otras palabras, un tema que parece sencillo, como el estudio de una partícula sumergida en un líquido macroscópicamente en reposo, es mucho más complicado de lo que parece. Y para describirlo se han construido modelos físicos y matemáticos con diferente grado de complejidad.
El modelo de camino al azar unidimensional discreto es un modelo muy simplificado para el fenómeno del movimiento browniano. En este modelo, en cada paso una partícula solo puede moverse con alguna probabilidad a la derecha o a la izquierda, con pasos discretos en el espacio y el tiempo. El límite continuo, en múltiples dimensiones espaciales, se encuentra más cerca del movimiento browniano. Pero dada la ubicuidad en la física del fenómeno del movimiento browniano, aún los modelos de camino al azar más sencillos encuentran múltiples aplicaciones, a veces en lugares tan inesperados como el estudio del crecimiento aleatorio de interfaces, el estudio de procesos de difusión en el océano (pueden encontrar en este link una aplicación a este tipo de problemas realizada por nuestro grupo de investigación), o en epidemiología (como veremos en un próximo posteo). En matemática el camino al azar también juega un rol importante a la hora de estudiar procesos estocásticos (Pablo Groisman, @pgroisma, en el Departamento de Matemática trabaja, entre otras cosas, en estos temas).
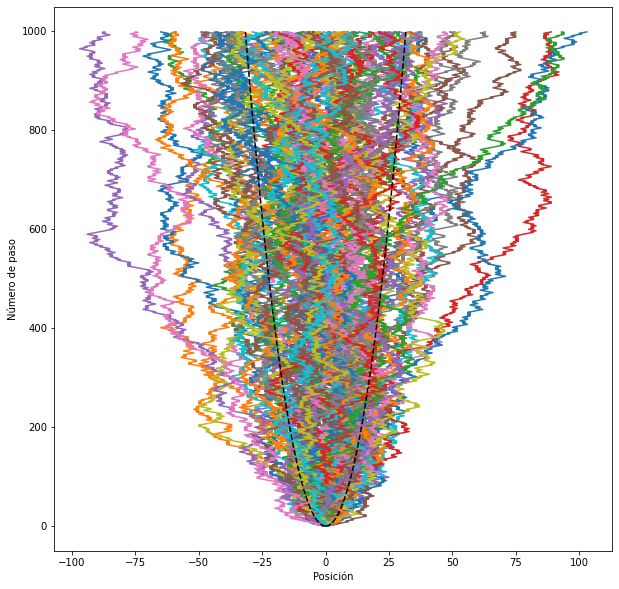
En física, un resultado importante de los modelos de camino al azar, y de la teoría de Einstein y Smoluchowski para el movimiento browniano, es la predicción de que el desplazamiento cuadrático medio de las partículas crece como la raíz del número de pasos (o del tiempo). El siguiente gráfico muestra 100 caminos al azar simétricos, y la predicción para el desplazamiento cuadrático medio:
Este resultado permite calcular el coeficiente de difusión para el sistema. Pero aunque parezca sencillo, este tampoco es un resultado trivial. Un coeficiente de difusión es una magnitud macroscópica (como la viscosidad de un líquido, o la conductividad eléctrica de un conductor), pero en este ejemplo el coeficiente macroscópico emerge como resultado de promediar sobre la trayectoria de muchas partículas individuales (y microscópicas). A lo largo de la materia veremos formas sistemáticas para calcular coeficientes efectivos de esta forma.