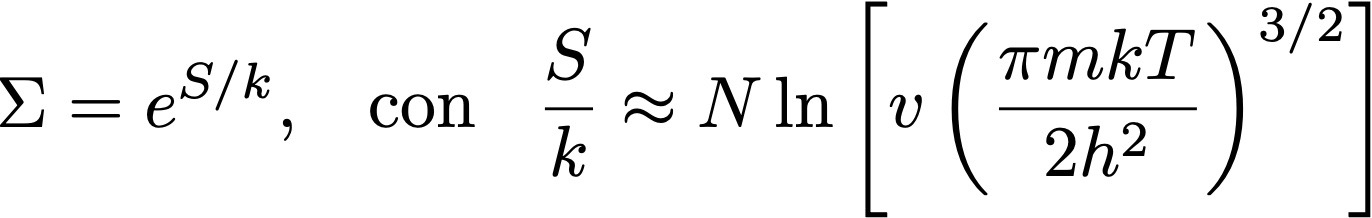“Ha llegado el momento de anunciar: Esta isla, con sus edificios, es nuestro paraíso privado. He tomado algunas precauciones -físicas, morales- para su defensa: creo que lo protegerán. Aquí estaremos eternamente -aunque mañana nos vayamos- repitiendo consecutivamente los momentos de la semana y sin poder salir nunca de la conciencia que tuvimos en cada uno de ellos.“

Adolfo Bioy Casares, La invención de Morel (1940).

El título del posteo de hoy hace referencia a Eterno resplandor de una mente sin recuerdos, película de 2004 dirigida por Michel Gondry en base a un guión de Charlie Kaufman. Los interesados en las repeticiones pueden ver también I’m Thinking of Ending Things en Netflix (dirigida por Charlie Kaufman), y Memento o Tenet (estas dos últimas dirigidas por Christopher Nolan). También pueden leer “La invención de Morel” de Adolfo Bioy Casares. Pero sepan que la repetición eterna, como los espejos y la cópula para un heresiarca de Uqbar, es abominable (excepto tal vez para Friedrich Nietzsche). Probablemente nos parezca antinatural justamente porque nunca observamos en la naturaleza que las configuraciones de sistemas extensos se repitan exactamente de la misma forma. Esta observación fue una de críticas que Poincaré y Zermelo, entre otros, realizaron a la teoría estadística de Boltzmann. Imagino que Sísifo también tendría sus objeciones. Y a Dormammu tampoco le deben gustar las repeticiones:

En el teorema H de Boltzmann, su entropía casi siempre crece. Imaginemos un gas que ocupa la mitad de un recinto, separado en dos por un tabique. En un dado instante el tabique se retira, y el gas se expande hasta ocupar todo el recinto (con el consecuente aumento de la entropía). Dado que todas las configuraciones son equiprobables, en algún instante todas las moleculas del gas podrían estar en la primera mitad del recinto (al fin y al cabo, podríamos tener configuraciones aún más extrañas). Pero si en ese preciso instante volvemos a poner el tabique, recuperamos en forma espontánea la primera configuración, que tenía menor entropía. Este posible retorno a una configuración previa fue visto por Poincaré como un problema abominable para la teoría de Boltzmann (aunque más tarde Poincaré se convenció del valor de la teoría y se retractó).

Efectivamente, si el número de configuraciones de un gas es discreto, existe una probabilidad no nula de que vuelva espontáneamente a una configuración previa (y si las configuraciones son contínuas, de que vuelva a una configuración arbitrariamente cercana a la configuración inicial). Pero el tiempo necesario para volver a encontrar esta configuración es increíblemente largo, lo que vuelve a este escenario irrelevante a fines prácticos. Estimemos esto para un metro cúbico de aire a temperatura ambiente (T = 300 K). Vimos que el número de configuraciones Σ de un gas ideal lo podemos calcular (en el ensamble microcanónico) como

donde S es la entropía, N el número de partículas, v el volúmen específico del gas, m la masa de las partículas (mayormente moléculas de N₂), k la constante de Boltzmann, y h la constante de Planck (ignoro un factor aditivo despreciable en la entropía). Usando valores típicos para estos parámetros (y considerando que v ≈ 5 x 10^-29 m³), obtenemos que el número de microestados o configuraciones posibles es

¡Este es un número enorme, con más de 10²⁵ dígitos! Asumamos ahora que las configuraciones cambian cada vez que hay un choque entre partículas. Es decir, cuando las partículas en el gas chocan, intercambian momento, y pasan de una configuración a otra. Como vimos en clase, para el aire a temperatura y presión ambiente, el tiempo entre choques es τ ≈ 10^-10 s. Y si todas las configuraciones son equiprobables, podemos estimar el tiempo medio para repetir una configuración como proporcional a Σ·τ, que sigue siendo un número muy grande (un tiempo con más de 10²⁵ dígitos, medido en segundos). ¡Como comparación, la edad del universo es de 4.3 x 10¹⁷ s, muchísimo más chica que el tiempo medio necesario para repetir la configuración de un gas en solo un metro cúbico! Por lo que el “casi siempre crece” de Boltzmann está bastante bien.

Hoy sabemos que aún en sistemas con tamaño finito, fuera del equilibro la probabilidad de que la entropía crezca es mucho más grande que la probabilidad de que la entropía disminuya. De hecho, sabemos que la razón entre estas dos probabilidades es igual a la exponencial de la variación de la entropía por el tiempo transcurrido, un número que se vuelve exponencialmente más grande a medida que la entropía del sistema crece, o que transcurre más tiempo. En el caso general este resultado se conoce como el teorema de fluctuación detallado.