Me imagino que todos quieren ser millonarios. ¡Pero seguro nunca se imaginaron que esta materia era la forma de alcanzar sus deseos! Salvo, obviamente, que hayan visto The hangover (2009), o películas un poco más serias como Rain Man (1988) y 21 (2008) (ambas basadas, con diversas libertades narrativas, en historias reales). En la última teórica vimos probabilidades. Las herramientas del curso se pueden usar para ganar en juegos de azar (¡o mejor aún, para evitarlos!), y para ilustrar cómo les cuento dos historias.
La primer historia es la del método para ganar en la ruleta de Edward Thorp (también creador de métodos para contar cartas en el blackjack) y Claude Shannon (el mismo Shannon de la entropía que veremos repetidas veces en la materia). Todos los juegos de azar en los casinos tienen esperanza negativa: si siguen jugando, a la larga solo pueden perder. En el caso de la ruleta, esto está relacionado con que un pleno (acertar a un número) paga 35 veces la apuesta, pero la probabilidad de acertar el número es 1/37 (pues la ruleta tiene 36 números más el cero). Así, en promedio, cada vez que apuestan pierden. El desafío es convertir la esperanza en positiva, es decir, saber con probabilidad mayor a 1/35 qué número va a salir. En los siguientes artículos Edward Thorp explica en detalle diversos métodos para ganar en la ruleta:
Los que quieran mas información sobre juegos de azar (y las siguientes entregas de estos artículos) pueden mirar la página web de Edward Thorp.
Básicamente existen tres tipos de métodos para la ruleta: (1) métodos matemáticos, (2) métodos basados en desperfectos de la ruleta, y (3) métodos predictivos basados en la física de la ruleta. Los primeros no son viables, ya que como mencioné arriba, los juegos de casino están diseñados para tener esperanza negativa. Para ser más claro: todo método que les cuenten basado solo en la matemática o la estadística o es mentira, o está explícitamente prohibido en las reglas del juego que usan los casinos. Al segundo método vamos a volver en un rato. El tercer camino es el que eligieron Thorp y Shannon.
En 1960 Thorp y Shannon usaron el hecho de que en los casinos se puede seguir apostando mientras la ruleta gira (y hasta que el crupier grita “¡No va más!”) para crear un algoritmo que basado en la velocidad de rotación de la ruleta, la velocidad de la bola, y su posición inicial aproximada (estimadas contando solo con inspección visual el número de vueltas que la ruleta y la bola dan en un período corto de tiempo), predice estadísticamente en qué octante de la ruleta puede caer la bola. En espíritu (aunque no en los detalles) esto es parecido a lo que vimos en el problema del camino al azar: no podemos saber dónde terminará la bola, pero nos alcanza con conocer la zona más probable de la ruleta en la que la bola puede terminar. Con esta información extra, la esperanza se vuelve positiva para el apostador. Pueden encontrar un artículo de divulgación con esta historia aquí:
Para realizar predicciones rápidas en el casino, Thorp y Shannon armaron una computadora pequeña, del tamaño de un atado de cigarrillos, que se llevaba con una faja en la cintura y se conectaba al zapato para ingresar los datos pisando fuerte o moviendo los dedos del pie. La siguiente foto muestra la pequeña computadora de Thorp y Shannon (la que se llevaba en la cintura):
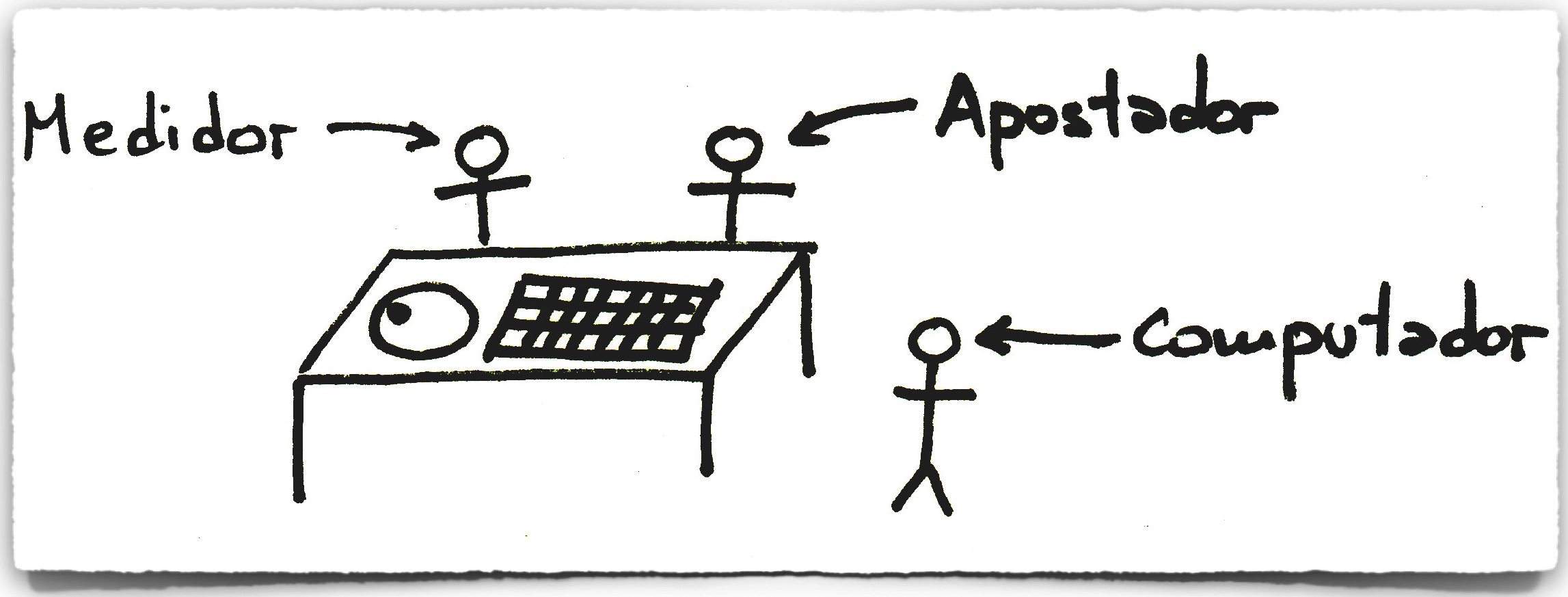
Otra persona (el apostador) usaba un pequeño receptor y un auricular para obtener la predicción y realizar rápidamente una apuesta. En la práctica, y para evitar ser detectados usaban a tres personas: una que medía, otra que llevaba la computadora, y el tercero que realizaba la apuesta, todos conectados por un sistema de radio:
¡Lo mas interesante es que el método funciona! Thorp y Shannon lo usaron con cierto éxito en Las Vegas. Una década más tarde un grupo de estudiantes de California perfeccionaría el sistema reduciendo aún más las computadoras y escondiéndolas completamente en zapatos (aquí pueden ver una imagen de las computadoras y encontrar algunos detalles sobre cómo funcionaban; el apostador ingresaba el período de rotación de la ruleta y el de la bola apretando un pulsador con el dedo del pie, y en otro zapato otra computadora devolvía la predicción del octante en el que caería la bola con una vibración). Todo esto además terminó siendo usado para el guión de un episodio de la serie original de Misión Imposible (1966), con un título insuperable:
La segunda historia tiene que ver con el segundo método para ganar en la ruleta, basado en desperfectos de la ruleta, e involucra a un estudiante de doctorado de Richard Feynman. Alrededor de 1940, Albert Hibbs y Roy Walford acumularon datos de jugadas en casinos de Reno y Las Vegas, para identificar algún pequeño bias o desperfecto en las ruedas de ruleta que favoreciera estadísticamente a ciertos números. Usando los datos estadísticos obtenidos para cada ruleta, Hibbs y Walford ganaron 8300 dólares en un día (las ruletas actuales no tienen este nivel de imperfección, por lo que el método ya no es aplicable hoy). Pueden leer una historia sobre Hibbs y Walford aquí:
Espero haberlos convencido, con estas historias, de que lo más conveniente es no apostar (salvo que uno esté dispuesto a esconder una computadora en un zapato). Para mostrar que más de 4000 físicos llegaron a la misma conclusión, les dejo un link a la famosa historia de la convención de físicos en Las Vegas que dió origen a la frase “They each brought one shirt and a ten-dollar bill, and changed neither”: