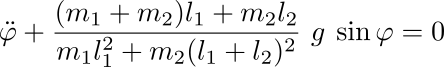Todos están familiarizados con el péndulo simple que muestra la figura: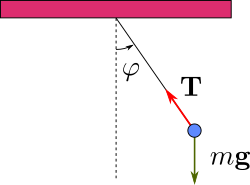
Las ecuación F = m a puede descomponerse en dos componentes, una paralela a la barra, que nos dice cuánto vale la tensión T, y otra perpendicular a la barra, que nos dice cuánto vale la aceleración angular. Esa es la ecuación de movimiento propiamente dicha, que se lee como: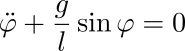
Todo bien con el péndulo simple. Pero imagínense que están en Física I y que les dan el siguiente péndulo doble “fijo”:
Este péndulo tiene la particularidad de que las barras no están articuladas. El ángulo φ puede variar pero las dos barras se mantienen alineadas. Seguramente (pensarán) debe ser más sencillo que el péndulo doble usual, porque hay una sola coordenada de la que preocuparse. Entonces, siempre en el contexto de Física I, construimos los diagramas de cuerpo libre para cada partícula. Lo más natural parece ser aplicar las mismas hipótesis que usamos para construir el diagrama de cuerpo libre del péndulo simple. Les quedan las siguientes dos figuras:
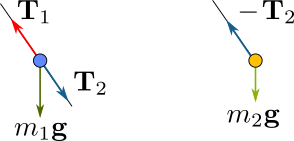
La proyección de las ecuaciones de movimiento en la dirección de la barra les vuelve a dar los valores de las tensiones, que aquí importan poco. En la dirección perpendicular a la barra, las únicas fuerzas que importan son los pesos. La aceleración de la primera partícula proyectada en la dirección perpendicular a la barra es![]()
y la de la segunda partícula es![]()
Los pesos proyectan según el seno del ángulo, de modo que, si todo está bien, las ecuaciones de movimiento para cada partícula son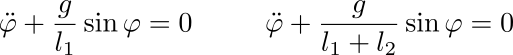
Aquí se ve que hay un problema. El ángulo no puede evolucionar al mismo tiempo según estas dos ecuaciones de movimiento. Algo hemos hecho mal. La pregunta es ¿dónde está el error? Como diría Paenza, deténganse aquí un momento y traten de pensar qué está pasando y qué cosa puede estar mal en las hipótesis que asumimos para llegar a estas dos ecuaciones contradictorias.
Veamos que nos dice la formulación lagrangiana. Las energías cinéticas son![]()
Por otro lado, las energías potenciales están dadas por![]()
Con esto, el lagrangiano resulta: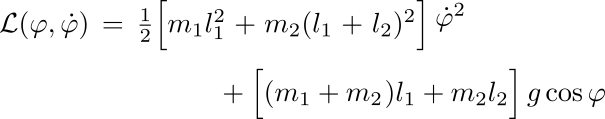
Recién estamos conociendo al formalismo lagrangiano, pero confiamos en que esta ecuación es la correcta. Es posible analizar varios límites. Por ejemplo, l2 = 0, m1 = 0. Todo parece andar bien.
Para terminar de convencernos de que la ecuación anterior es correcta, hay otra manera de deducirla con métodos de Física I, a partir de la ecuación para la variación del momento angular en términos de los torques. Después de todo, este sistema es lo que llamaríamos un péndulo físico. Deberían poder verificarlo rápidamente y así convencerse de que la ecuación anterior es la correcta.
Saber que la ecuación está bien no resuelve el misterio de por qué las otras dos ecuaciones estaban mal. La pregunta persiste: ¿por qué está mal el primer procedimiento? Un camino para llegar a la respuesta es usar la ecuación de movimiento correcta para encontrar las fuerzas de vínculo sobre cada partícula. No es difícil y la solución es bastante esclarecedora, así que les recomiendo que lo hagan. Hay un punto clave que es mejor dejar que ustedes descubran.