En el problema 15 de la Guía 7, se pide demostrar que, para una partícula, si se conservan dos componentes del momento angular, entonces se conserva la tercera. La indicación de que se trata de una partícula sirve para fijar la definición de L,
Por componentes, se entiende que se trata de las componentes cartesianas. La demostración es una aplicación muy sencilla de la identidad de Jacobi y del hecho de que el corchete de dos componentes distintas de L es, quizá a menos de un signo, igual a la tercera.
Ahora bien, consideren una partícula en caída libre en un campo gravitatorio uniforme, como muestra la figura. La partícula viaja a lo largo de la recta x = x0, y = 0. 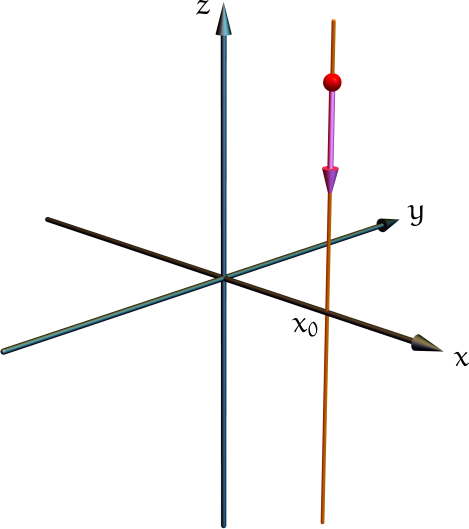
Su posición en función del tiempo es
Su velocidad es![]() Luego, su momento angular resulta
Luego, su momento angular resulta![]()
Ocurre entonces que dos componentes de L se conservan,![]()
pero la tercera no se conserva,![]()
¿Dónde está la trampa?

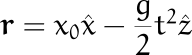

Podés tomar x0 = 0. Entonces se conservan las 3 componentes.
No, no podés. Si x0 = 1, no podés decir que x0 = 0. x0 es lo que es.
Para mí porque no es verdad que Lx, Lz sean ctes. Estás usando la solución r(t) de ese sist ref particular (no el teo de Poisson u otro arg) para decir que se conservan Lx, Lz. Pero L sí depende del sist ref; uno con v cte en dirección “y” va a decir que Lx,Lz valen otra cosa y tamb sus torques. Con el teo de Poisson eso se puede hacer porque la derivada temporal da cero indep de qi, pi,t canónicas que tomés, aseguras que es una propiedad del sistema pero al revés no.
Lx y Lz son constantes. ¿Cómo que no? No tiene nada que ver con el sistema de referencia. Una cosa es que los corchetes de Poisson no dependan del conjunto de coordenadas {q, p}. Otra cosa es cambiar sistemas de referencia. Lo único que tiene un poco de sentido es decir “aseguras que es una propiedad del sistema”, pero no sé si por las razones correctas.
Tenés razón, me expresé mal, quise decir que no está probado que Lx y Lz sean constantes de movimiento. Ahí sólo se muestra que son ctes usando r(t) pero eso es particular.
Eso sí tiene sentido.