Supongan que tienen un sistema cuyo lagrangiano es igual a la energía cinética,
![]() Puede ser, por ejemplo, una partícula libre en coordenadas esféricas, para que no sea tan trivial; o una partícula que se mueve sobre una superficie, sometida sólo a la fuerza de vínculo. En general, las ecuaciones de Euler-Lagrange son
Puede ser, por ejemplo, una partícula libre en coordenadas esféricas, para que no sea tan trivial; o una partícula que se mueve sobre una superficie, sometida sólo a la fuerza de vínculo. En general, las ecuaciones de Euler-Lagrange son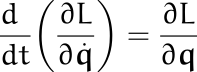 Usando la definición del momento conjugado, esto también puede escribirse como
Usando la definición del momento conjugado, esto también puede escribirse como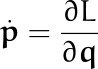 Para el caso específico que estamos analizando, queda
Para el caso específico que estamos analizando, queda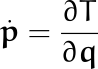 Por ejemplo, en el caso de la partícula libre en coordenadas esféricas
Por ejemplo, en el caso de la partícula libre en coordenadas esféricas![]() y una de las ecuaciones es
y una de las ecuaciones es![]() que claramente no tiene por qué ser cero, aunque la partícula sea libre. Hasta aquí todo parece en orden. Los problemas surgen cuando intentamos comparar las ecuaciones de movimiento del formalismo lagrangiano con las del formalismo hamiltoniano.
que claramente no tiene por qué ser cero, aunque la partícula sea libre. Hasta aquí todo parece en orden. Los problemas surgen cuando intentamos comparar las ecuaciones de movimiento del formalismo lagrangiano con las del formalismo hamiltoniano.
Asumiendo que T es una función homogénea de grado 2 en las velocidades, el hamiltoniano de este problema es simplemente![]()
En general, la ecuación de Hamilton para los impulsos conjugados es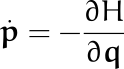
En el caso específico que estamos considerando, resulta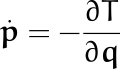 Pero esta ecuación tiene justo el signo contrario de la que escribimos anteriormente
Pero esta ecuación tiene justo el signo contrario de la que escribimos anteriormente
Ya vimos con un ejemplo que, en general, la derivada de p no es cero. Entonces, ¿cuál es la ecuación correcta?

