Las ecuaciones de Euler-Lagrange se deducen usualmente a partir del principio de D’Alembert: el trabajo de las fuerzas de vínculo durante un desplazamiento virtual es nulo. El propio Lagrange trató en varias ocasiones de demostrar este principio, pero sus demostraciones son vanas. La mecánica lagrangiana surge de la conjunción de las leyes de Newton y del principio de los trabajos virtuales. La mecánica lagrangiana no es una presentación nueva de las leyes de Newton.
De manera que tienen tanto derecho a sentirse incómodos con el principio de D’Alembert como a sentirse incómodos con los axiomas de Euclides o con los de la mecánica cuántica. Lo digo seriamente.
Aquí les dejo un par de citas de libros muy recomendables. Pueden hacer click en las imágenes para ampliarlas. La primera cita es de Sommerfeld (Mechanics, 1952, pp. 52-53):
En el mismo espíritu, Lanczos dice lo siguiente (The variational principles of mechanics, 1949, p. 77):
El postulado A del que habla Lanczos es el principio de D’Alembert.
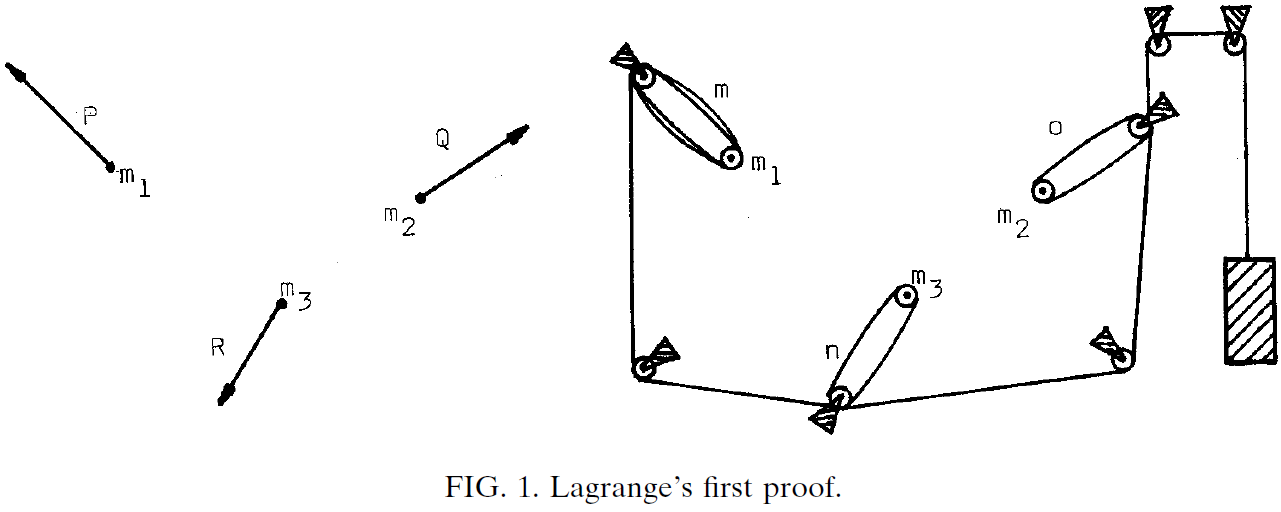
La figura que encabeza esta entrada está basada en una de las demostraciones del principio de los trabajos virtuales ofrecida por Lagrange, que nunca hizo ese dibujo ni ningún otro. Para Lagrange era cuestión de honor hacer todo de manera analítica, sin el auxilio de figuras.