Ejemplo: potencial V = (Tan x)2.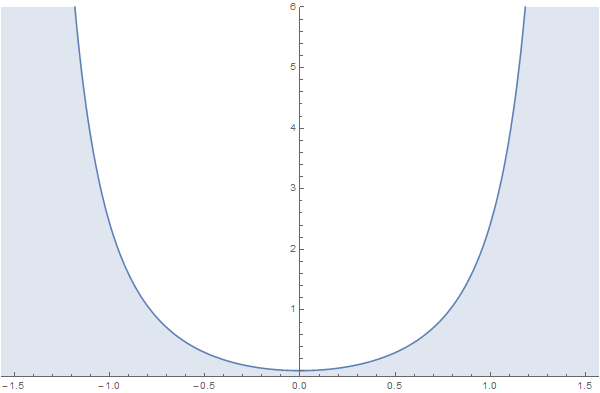
Órbitas en el espacio de fases: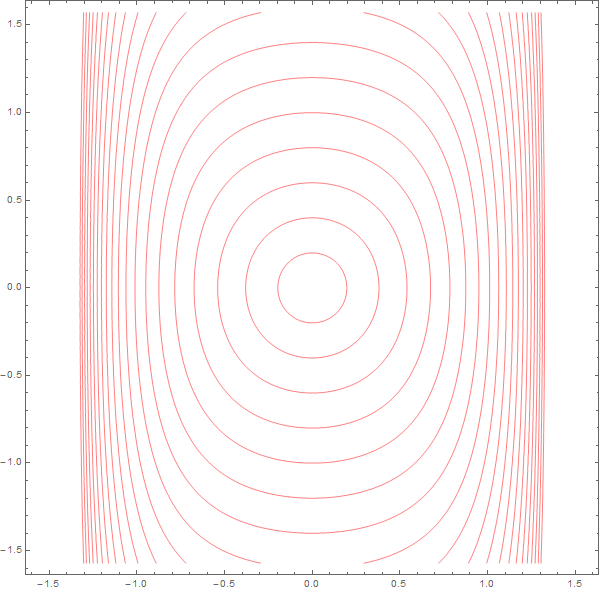
Animación 1: el movimiento dependiendo de la energía de la partícula. En este potencial, a mayor amplitud, menor es el período.
Animación 2 (abrir en una nueva ventana): la construcción de las coordenadas canónicas (Q, E) asociadas a la función generatriz W(x, E).
En el plano (x, p) las líneas coordenadas (Q, E) toman el siguiente aspecto, válido para el movimiento durante un sólo período.
Sobre cada órbita (curvas llenas) el intervalo de tiempo entre dos cruces sucesivos es constante e igual para todas las órbitas. Como las partículas se mueven a velocidades muy diferentes eso produce una enorme distorsión.
Animación 3 (abrir en una nueva ventana): la construcción de las coordenadas de ángulo-acción.
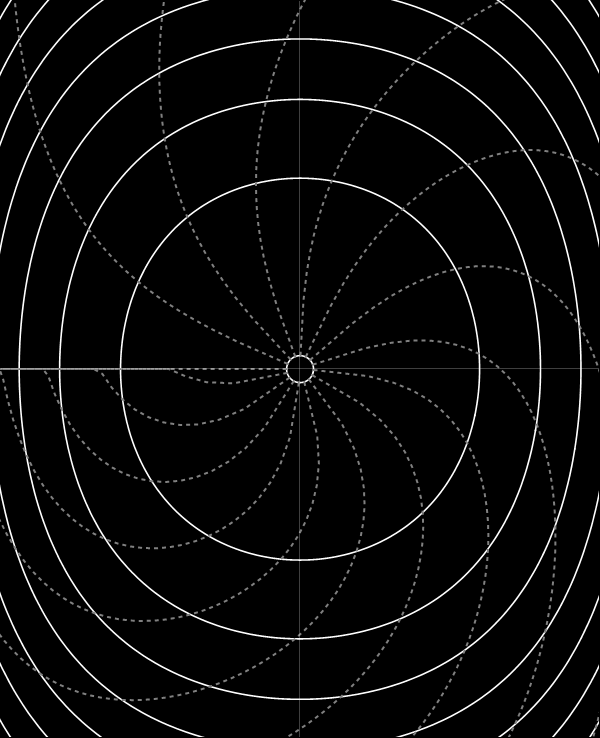
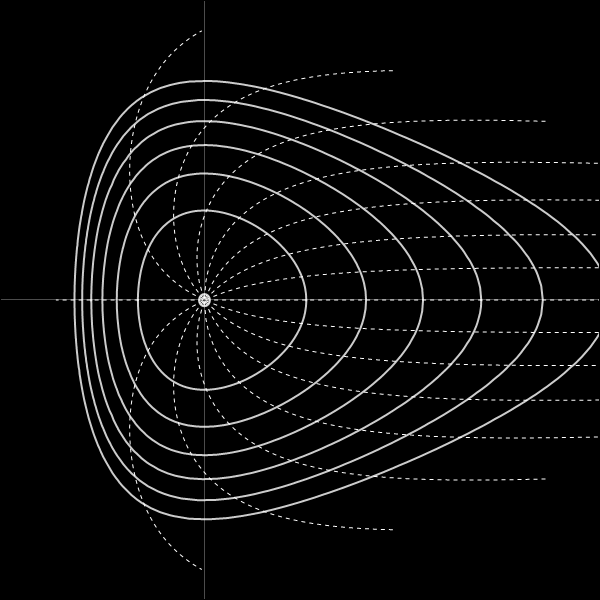
En el plano (x, p) las líneas coordenadas (θ, J) toman el siguiente aspecto.
A lo largo de cada órbita (curvas llenas) cada cruce con las líneas de θ constante (curvas punteadas) se produce a intervalos regulares de tiempo, iguales a una fracción fija del período de la órbita (en este caso se tomó esa fracción igual a 1/12). Lo mismo vale para cada órbita. Se produce en efecto una normalización respecto del período: cruces sucesivos de las curvas de θ constante representan la misma fracción del período para todas las órbitas, pero como estos períodos difieren entonces el tiempo entre cruces sucesivos varía con la órbita considerada. Todas las órbitas comienzan y se cierran en los mismos valores de θ.
Ejemplo: problema efectivo para el movimiento radial en el potencial V = -k/r.
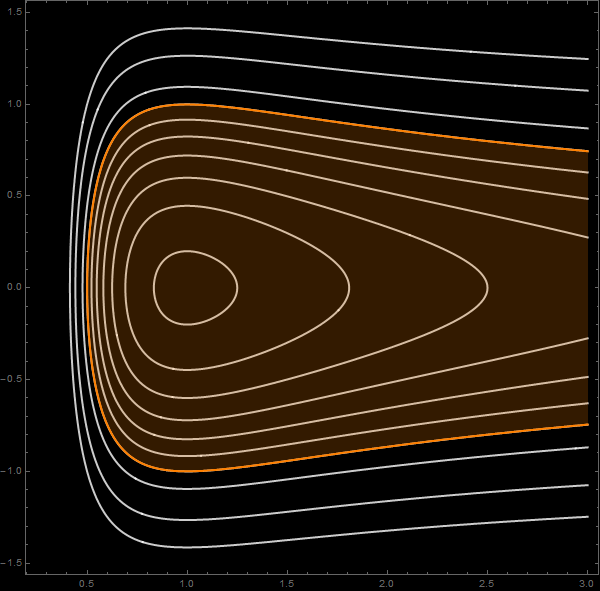
El retrato de fases muestra que hay regiones de movimiento acotado y no acotado. La figura muestra las órbitas y la separatriz:
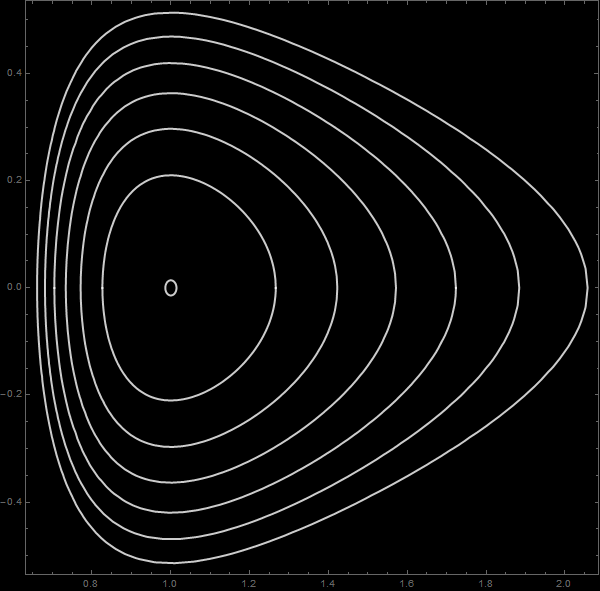
Las variables de ángulo-acción sólo pueden definirse en el primer caso. La figura muestra un detalle de esta región:
Mediante el procedimiento de integrar numéricamente las ecuaciones de movimiento de un grupo de partículas con distintos valores de la energía (es decir, se mueven sobre órbitas distintas), y de marcar sobre cada órbita las posiciones a intervalos de una fracción fija del período correspondiente se consiguen graficar las curvas de θ constante (curvas punteadas):