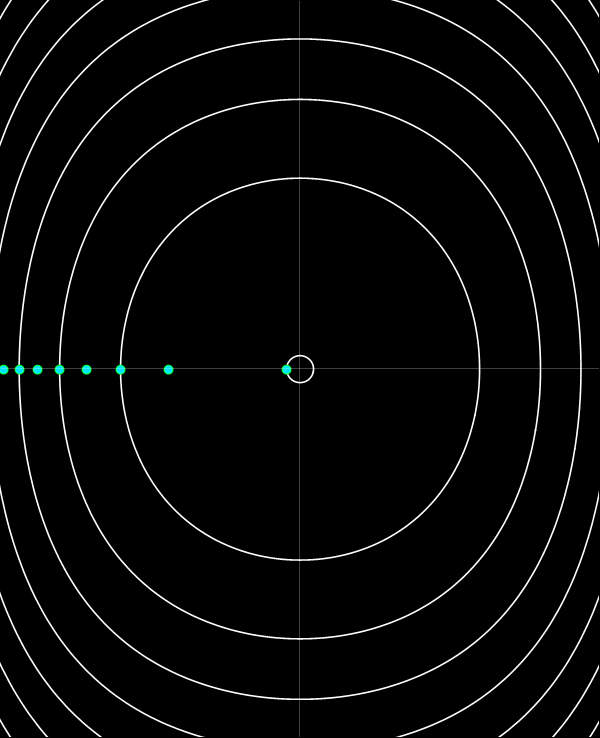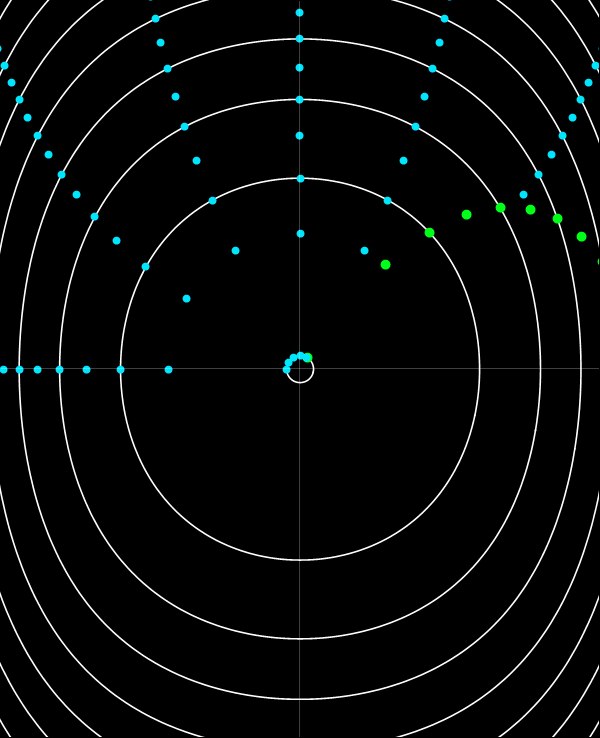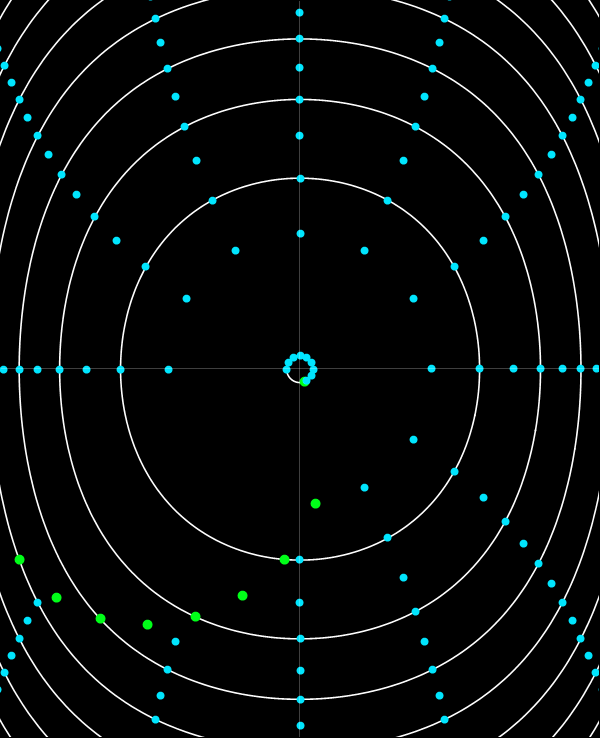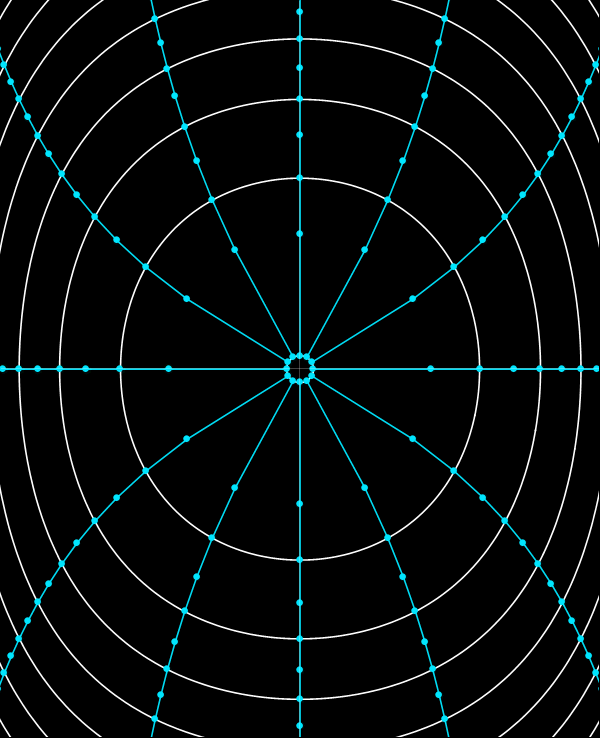
Mediante el cambio de variable de E a J en la función generatriz W(x, E) se obtiene una transformación a las coordenadas de ángulo-acción, θ y J. Como J es función sólo de E, las curvas coordenadas de J constante son las mismas curvas de E constante. La variable ángulo tiene la misma propiedad que Q de aumentar uniformemente con el tiempo, pero lo hace, a diferencia de Q,  con una velocidad que depende de le energía: dθ/dt = dE/dJ. Esta dependencia es tal que θ varía en 2π a lo largo de un período, independientemente de la energía de la órbita. Dada una órbita en particular, si dividimos el período de la órbita en n intervalos iguales y marcamos la posición de la partícula al comienzo de cada intervalo, estaremos marcando puntos equiespaciados en θ. Si se repite este procedimiento para otras energías conseguiremos marcar puntos sobre las curvas de θ constante.

La animación de abajo se construyó soltando un conjunto de partículas desde sus puntos de retorno y marcando sus posiciones a intervalos de 1/12 veces el período de cada órbita.  (Notar que la animación solo se reproduce una vez. Actualizar la página o hacer click en la imagen para reproducir de nuevo la animación.)