La función generatriz W(x, E) da la transformación entre las coordenadas (x, p) y las coordenadas (Q, E). En las nuevas coordenadas el hamiltoniano es K(Q, E) = E, y por lo tanto la coordenada Q tiene la dependencia temporal Q = t + cte. El hecho importante aquí es que la velocidad de variación de Q es independiente de la energía.
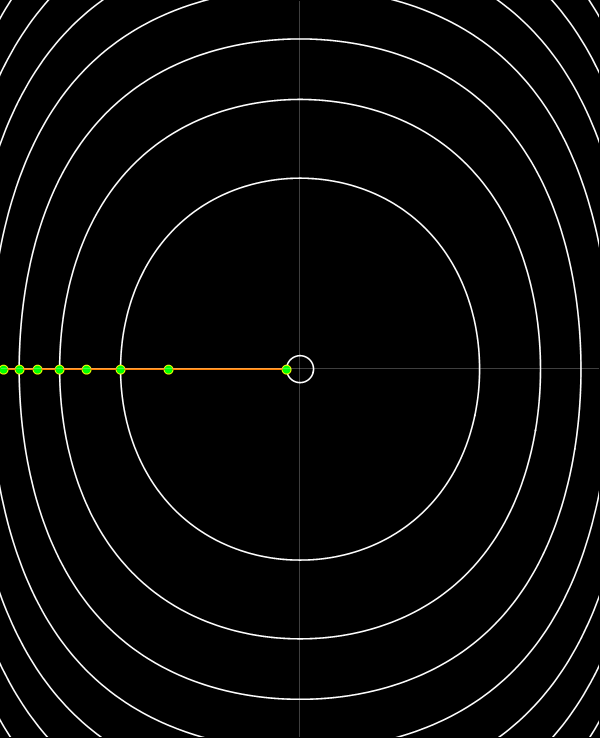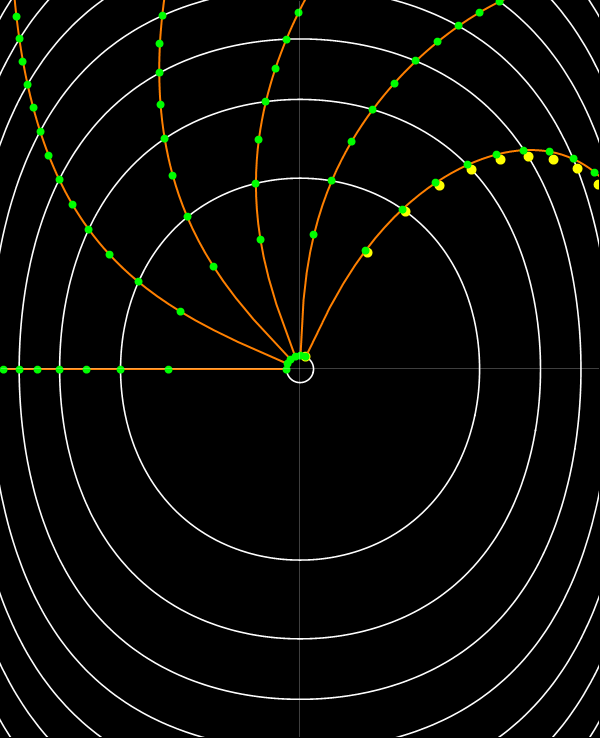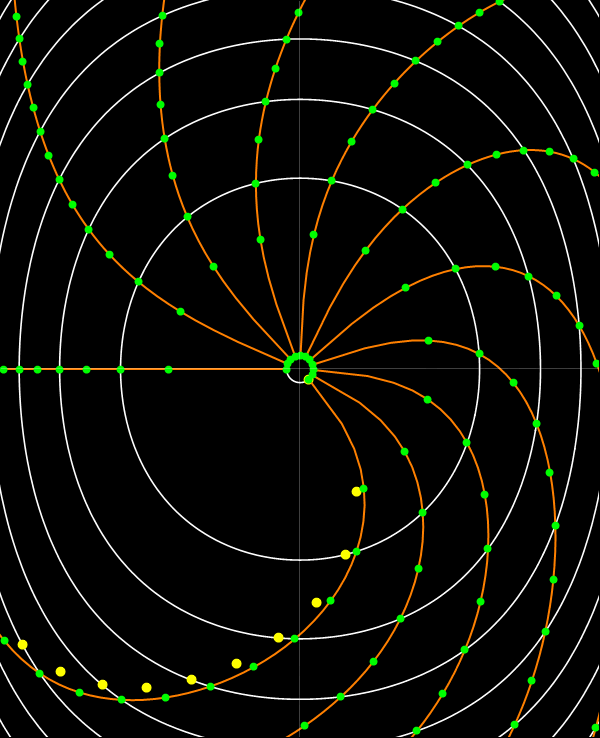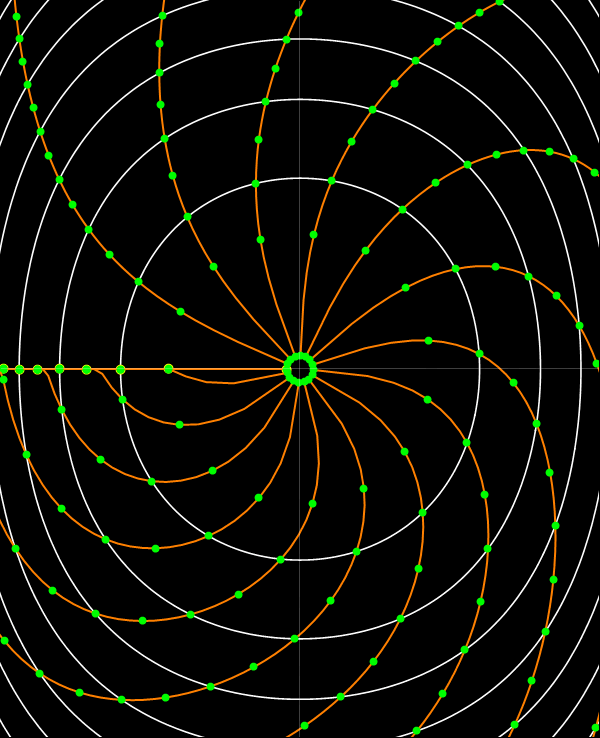
En el espacio de fases (x, p) las curvas coordenadas de E constante son fáciles de construir, son las curvas de nivel de la función p2 + (Tan x)2. Las curvas de Q constante pueden construirse del siguiente modo.
Puesto que Q avanza uniformemente con el tiempo, si liberamos un conjunto de partículas en t = 0 desde una posición de referencia y marcamos sus posiciones a intervalos fijos de t, estas posiciones estarán sobre las curvas de Q constante. En la animación, la posición de referencia de partida es uno de los puntos de retorno. Como las partículas con más energía adelantan a las que tienen menos, las curvas de nivel de Q tienen un aspecto espiralado. (Notar que la animación solo se reproduce una vez. Actualizar la página o hacer click en la imagen para reproducir de nuevo la animación.)