En la Guía 7, uno de los primeros problemas es analizar el espacio de fases reducido de una peonza simétrica, con un punto fijo y gravedad. Hay suficientes cantidades conservadas como para formular un problema unidimensional equivalente en el ángulo de Euler θ. Aun así, las trayectorias en el espacio de fases θ-pθ dependen de varios parámetros. En clase estudiamos el caso pφ = pΨ, y redujimos el número de parámetros a 1. Ustedes deberían analizar otros casos sencillos.

El retrato de fases en el plano θ-pθ tomaba dos aspectos cualitativamente distintos dependiendo de la relación entre la gravedad y el efecto estabilizador del espín. Pero saber qué hacen las coordenadas  θ-pθ no permite de manera inmediata tener una idea de cómo es el movimiento real de la peonza en el espacio 3D. Las siguientes animaciones fueron hechas con este propósito.

• Primer caso: con un bajo valor de la gravedad en relación al espín. Hay un solo punto de equilibrio, que es estable. El problema está gobernado por la rotación de la peonza.
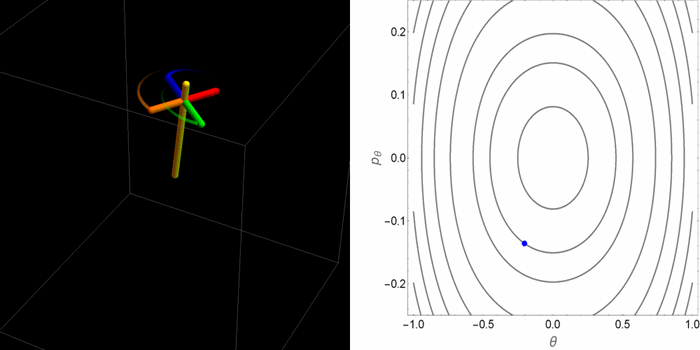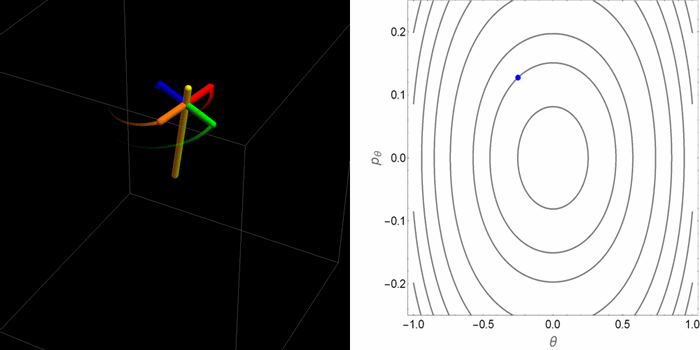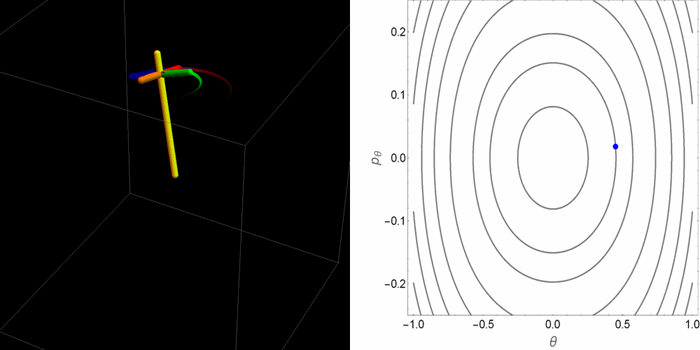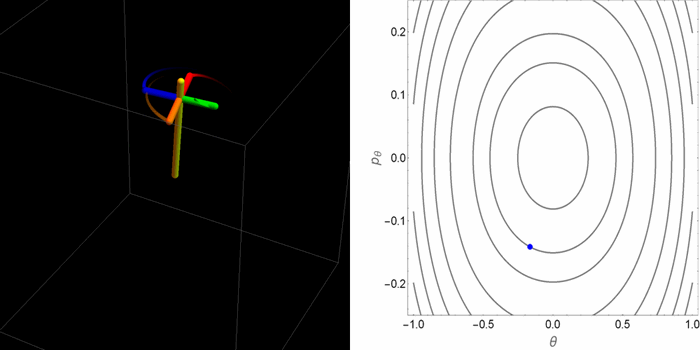
• Segundo caso: un valor alto de la gravedad y, en particular, una condición inicial que mantiene a la peonza orbitando alrededor de uno de los puntos de equilibrio estable del espacio  θ-pθ. No obstante, la peonza se acerca bastante al punto de equilibrio inestable en el origen, donde se demora brevemente antes de caer. 
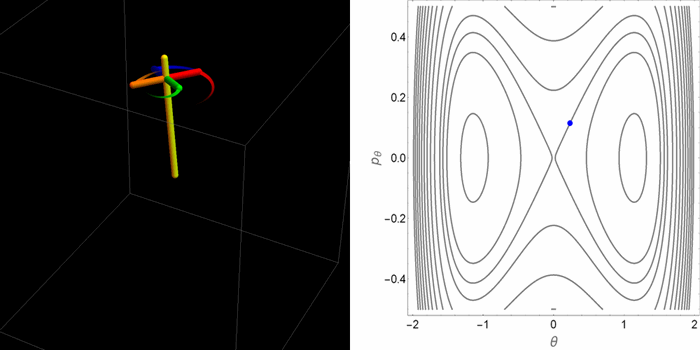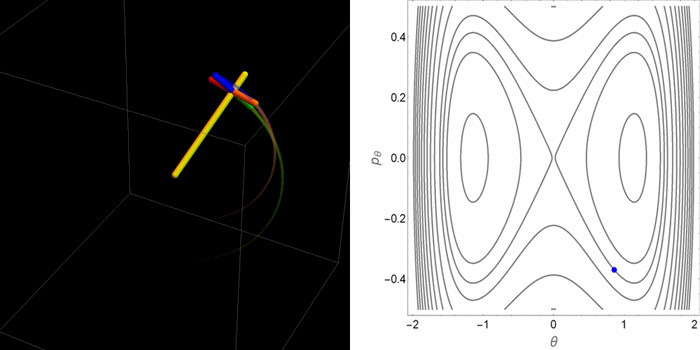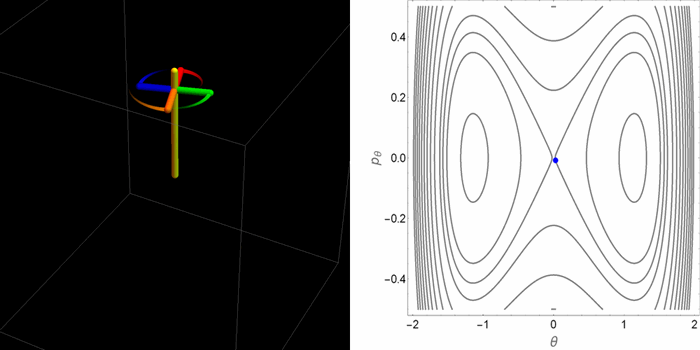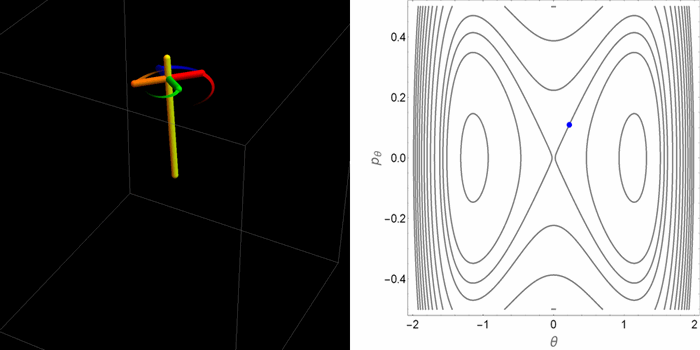
• Tercer caso: un valor alto de la gravedad y una condición inicial por fuera de la curva separatriz que divide las órbitas en el espacio  θ-pθ. Ahora  en el espacio  θ-pθ la peonza orbita alrededor de los tres puntos de equilibrio.

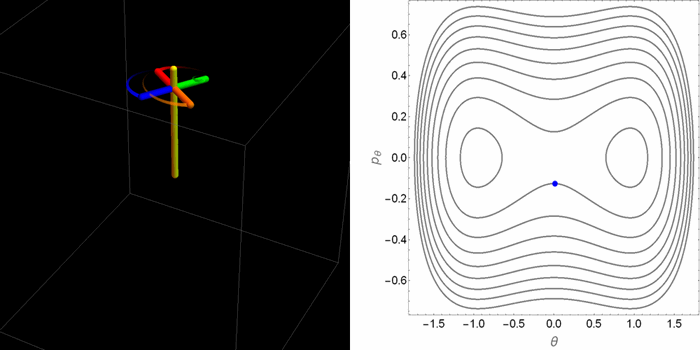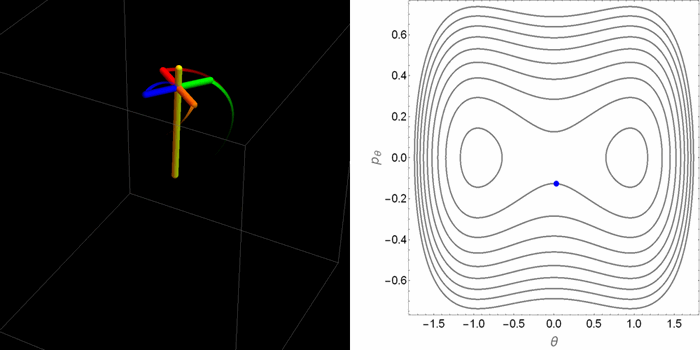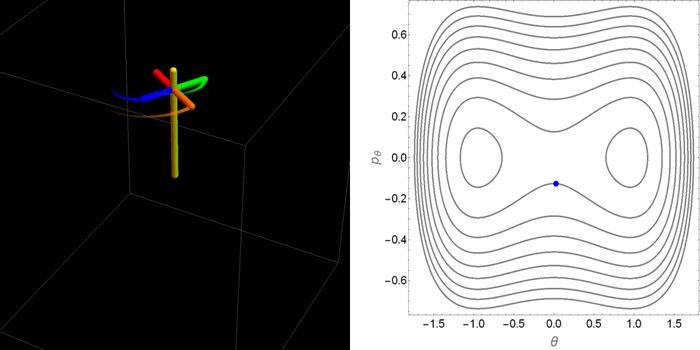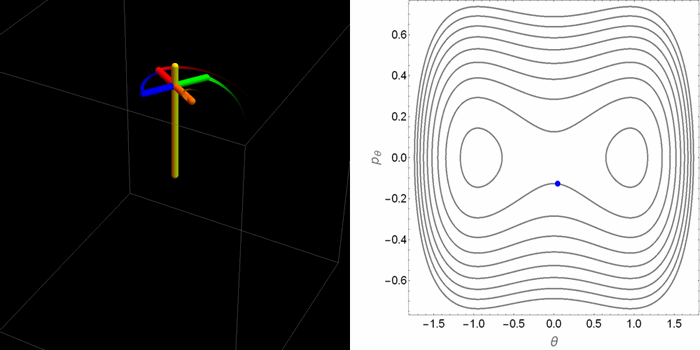
Aunque estos casos agotan las alternativas posibles, dentro de estas alternativas hay muchos matices. Por ejemplo, dependiendo de las condiciones iniciales la órbita puede ser cerrada o abierta en el espacio tridimensional. En el plano  θ-pθ la proyección siempre es una órbita cerrada. De las tres animaciones anteriores, hay una sola que se cierra sobre sí misma.

[Aquí] les dejo el archivo del Mathematica con el que hice las animaciones. Además de servir como guía para los que recién están usando el programa, sirve también como registro escrito de la clase del jueves pasado. Para los que no tienen aún el Mathematica, [aquí] les dejo una versión pdf del notebook, que les puede venir bien como apunte para este problema, independientemente de que quieran o no usar el Mathematica.