Física Teórica 2
Primer cuatrimestre de 2019
Guía 6: Rotaciones y Momento Angular

Representación de Rotaciones y Momento Angular en Mecánica Cuántica

  1. Sea \(\boldsymbol{\mathbf{J}} = \left(J_x, J_y, J_z\right)\) un operador de momento angular, es decir que sus componentes satisfacen las relaciones de conmutación \[\left[{J_j},{J_k}\right] = i\hbar\,\varepsilon_{jkl}\,J_l.\]

    1. Se definen los operadores de subida (\(J_+\)) y bajada (\(J_-\)) de la forma \[J_+ = J_x + iJ_y, \qquad J_- = J_x - iJ_y.\] Demostrar las siguientes propiedades \[\begin{aligned} \left[{J^2},{J_i}\right] &= 0, \qquad \left[{J_z},{J_\pm}\right] = \pm \hbar J_\pm, \qquad \left[{J_+},{J_-}\right] = 2\hbar J_z, \\ J_+ J_- &= J^2 - J_z^2 + \hbar J_z, \qquad J_- J_+ = J^2 - J_z^2 - \hbar J_z. \end{aligned}\]

    2. Sea \(\left\{\left|{j,m}\right\rangle\right\}\) la base de autoestados simultáneos de \(J^2\) y \(J_z\), es decir que \[J^2\left|{j,m}\right\rangle = \hbar^2 j(j+1)\left|{j,m}\right\rangle, \qquad J_z\left|{j,m}\right\rangle = \hbar m\left|{j,m}\right\rangle.\] Demostrar las siguientes propiedades \[J_\pm \left|{j,m}\right\rangle = \hbar\sqrt{j(j+1)-m(m\pm1)} \left|{j,m \pm 1}\right\rangle, \qquad J_\pm \left|{j,\pm j}\right\rangle = 0 .\]

  2. Suponga que un sistema se encuentra en un autoestado de \(J_z\) con autovalor \(\hbar m\).

    1. Muestre que los valores medios tanto de \(J_x\) como \(J_y\) son cero, i.e. \(\left\langle{J_x}\right\rangle = \left\langle{J_y}\right\rangle = 0\), de dos formas diferentes: (i) usando el principio de incertidumbre, y (ii) usando la expansión de \(J_x\) y \(J_y\) en términos de \(J_+\) y \(J_-\).

    2. Muestre que si se mide la projección de momento angular en la sobre una dirección \(\boldsymbol{\mathbf{\hat{n}}}\) que forma un ángulo \(\theta\) con el eje \(\boldsymbol{\mathbf{\hat{z}}}\), entonces \[\left\langle{\boldsymbol{\mathbf{J}}\cdot\boldsymbol{\mathbf{\hat{n}}}}\right\rangle = \hbar m\cos\theta.\]

  3. Considere un sistema de spin \(1/2\) (es decir \(j = 1/2\)).

    1. Construya, por aplicación de los operadores de subida y bajada, la representación matricial de los operadores \(S^2\), \(S_x\), \(S_y\) y \(S_z\) en la base de autoestados de \(S_z\). Muestre que se obtiene que los operadores de spin están dados por \(S_i = \frac{\hbar}{2}\sigma_i\), donde \(\sigma_i\) son las matrices de Pauli.

    2. Usando las propiedades de conmutación (\(\left[{\sigma_j},{\sigma_k}\right] = 2i\varepsilon_{jkl}\sigma_l\)) y anticonmutación (\(\left\{{\sigma_j},{\sigma_k}\right\} = 2\delta_{jk}\mathbb{I}\)) de las matrices de Pauli, pruebe la identidad \[(\boldsymbol{\mathbf{\sigma}}\cdot\boldsymbol{\mathbf{a}})(\boldsymbol{\mathbf{\sigma}}\cdot\boldsymbol{\mathbf{b}}) = \left(\boldsymbol{\mathbf{a}}\cdot\boldsymbol{\mathbf{b}}\right)\mathbb{I}+ i\boldsymbol{\mathbf{\sigma}}\cdot(\boldsymbol{\mathbf{a}}\times\boldsymbol{\mathbf{b}}),\] donde \(\boldsymbol{\mathbf{a}}\) y \(\boldsymbol{\mathbf{b}}\) son dos vectores complejos en tres dimensiones. (Ayuda: recuerde que \((\boldsymbol{\mathbf{a}}\times\boldsymbol{\mathbf{b}})_i = \sum_{ijk}\varepsilon_{ijk}a_jb_k\) y que todo producto de dos operadores se puede reescribir como \(AB = (\left[{A},{B}\right] + \left\{{A},{B}\right\})/2\)).

    3. Usando los resultados anteriores, muestre que el operador rotación para un sistema de spin \(1/2\) se puede escribir como \[\RotationOp[(1/2)](\boldsymbol{\mathbf{\hat{n}}},\phi) = \exp\left(-i\, \frac{\boldsymbol{\mathbf{S}} \cdot \boldsymbol{\mathbf{\hat{n}}}\, \phi}{\hbar} \right) = \mathbb{I}\cos(\frac{\phi}{2}) - i \left(\boldsymbol{\mathbf{\sigma}}\cdot\boldsymbol{\mathbf{\hat{n}}}\right) \sin(\frac{\phi}{2}),\] donde \(\mathbb{I}\) es la matriz identidad.

    4. Escriba explícitamente la matriz de \(2\times2\) que representa la rotación \(\RotationOp[(1/2)](\boldsymbol{\mathbf{\hat{n}}},\phi)\) en la base \[\left\{\left|{+}\right\rangle \equiv \left|{j = {\frac{1}{2}}, m = {\frac{1}{2}}}\right\rangle, \left|{-}\right\rangle \equiv \left|{j = {\frac{1}{2}}, m = {-\frac{1}{2}}}\right\rangle\right\}.\]

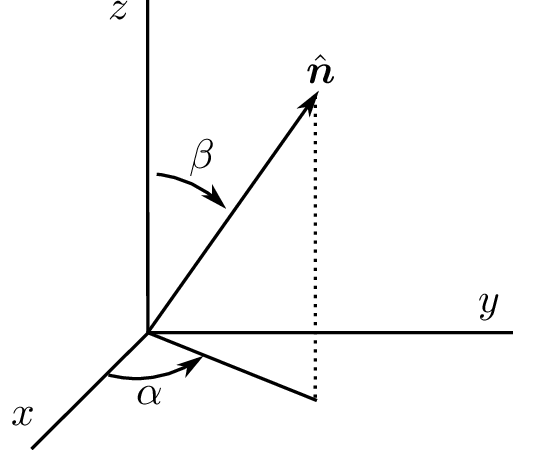
    5. Sea \(\boldsymbol{\mathbf{\hat{n}}}\) el versor definido por los ángulos polares \(\alpha\) y \(\beta\) según se muestra en la figura. Aplique al ket \(\left|{+}\right\rangle\) el operador de rotación adecuado\({}^\dagger\) para obtener el estado \(\left|{\boldsymbol{\mathbf{S}} \cdot \boldsymbol{\mathbf{\hat{n}}},+}\right\rangle\), que representa un spin orientado según \(\boldsymbol{\mathbf{\hat{n}}}\). Compare el resultado con el obtenido en el Problema 10 de la Guía 1.

      image

      \({}^\dagger\) Pruebe a hacer la cuenta de dos formas diferentes: (i) aplicando una única rotación en una ángulo y dirección adecuados, y (ii) descomponiendo la rotación en rotaciones elementales utilizando los ángulos de Euler.

    6. Muestre que para una rotación en \(\phi = 2\pi\) se satisface \[\RotationOp[(1/2)](\boldsymbol{\mathbf{\hat{n}}},\phi=2\pi) = -\mathbb{I},\] y, por lo tanto, ante una rotación en \(2\pi\) el estado del sistema cambia según \[\left|{\psi}\right\rangle \xrightarrow[\RotationOp(\boldsymbol{\mathbf{\hat{n}}},2\pi)]{} \RotationOp[(1/2)](\boldsymbol{\mathbf{\hat{n}}},2\pi)\left|{\psi}\right\rangle = -\left|{\psi}\right\rangle.\] Observe que no se obtiene el mismo vector debido a un factor de fase. ¿Puede observarse este efecto? Vea Phys. Rev. Lett 35, 1053 (1975), o Phys. Today, Dic. 1980, pág. 24.

  4. Considere un estado arbitrario \(\left|{\psi}\right\rangle\) de un sistema de spin \(1/2\), sobre el que se aplica una rotación en un ángulo \(\varphi\) alrededor del eje \(\boldsymbol{\mathbf{\hat{z}}}\), es decir \[\left|{\psi}\right\rangle \longrightarrow \left|{\psi'}\right\rangle = \RotationOp[(1/2)](\boldsymbol{\mathbf{\hat{z}}},\varphi)\left|{\psi}\right\rangle = \exp\left(-i\,\frac{S_z\varphi}{\hbar}\right)\left|{\psi}\right\rangle.\] Calcule los valores medios \(\left\langle{\psi'}\middle|{S_x}\middle|{\psi'}\right\rangle\), \(\left\langle{\psi'}\middle|{S_y}\middle|{\psi'}\right\rangle\) y \(\left\langle{\psi'}\middle|{S_z}\middle|{\psi'}\right\rangle\) en el sistema rotado, en función de los valores de expectación \(\left\langle{\psi}\middle|{S_x}\middle|{\psi}\right\rangle\), \(\left\langle{\psi}\middle|{S_y}\middle|{\psi}\right\rangle\) y \(\left\langle{\psi}\middle|{S_z}\middle|{\psi}\right\rangle\) en el sistema original.

  5. Considere la secuencia de rotaciones de Euler de un sistema de spin \(1/2\) representada por \[\RotationOp(\alpha,\beta,\gamma) = \RotationOp(\boldsymbol{\mathbf{\hat{z}}},\alpha)\, \RotationOp(\boldsymbol{\mathbf{\hat{y}}},\beta)\, \RotationOp(\boldsymbol{\mathbf{\hat{z}}},\gamma).\]

    1. Muestre que la matriz de \(2\times2\) que representa esta rotación es \[\begin{aligned} \RotationOp[(1/2)](\alpha,\beta,\gamma) &= \exp\left(-i \frac{\sigma_z \alpha}{2}\right) \exp\left(-i \frac{\sigma_y \beta}{2}\right) \exp\left(-i \frac{\sigma_z \gamma}{2}\right) \\ &= \begin{pmatrix} e^{-i(\alpha+\gamma)/2} \cos\frac{\beta}{2} & -e^{-i(\alpha-\gamma)/2} \sin\frac{\beta}{2} \\ e^{i(\alpha-\gamma)/2} \sin\frac{\beta}{2} & e^{i(\alpha+\gamma)/2} \cos\frac{\beta}{2} \\ \end{pmatrix} . \end{aligned}\]

    2. Debido a las propiedades del grupo de las rotaciones, esperamos que esta secuencia de operaciones sea equivalente a una única rotación alrededor de algún eje con ángulo \(\theta\). Encuentre \(\theta\) y la dirección de dicho eje.

  6. Considere un sistema con momento angular 1 (es decir, \(j = 1\)).

    1. Construya, por aplicación de los operadores de subida y de bajada, la representan matricial de los operadores \(J^2\), \(J_x\), \(J_y\), y \(J_z\) en la base \(\left\{\left|{j = {1}, m = {1}}\right\rangle, \left|{j = {1}, m = {0}}\right\rangle, \left|{j = {1}, m = {-1}}\right\rangle\right\}\) de autoestados de \(J^2\) y \(J_z\). Verifique explícitamente multiplicando las matrices la relación \(\left[{J_x},{J_y}\right] = i \hbar J_z\).

    2. Encuentre la base \(\left\{\left|{j=1,m_y}\right\rangle\right\}\) de autoestados de \(J^2\) y \(J_y\), como combinación lineal de los \(\left\{\left|{j=1,m}\right\rangle\right\}\).

    3. Evalúe los elementos de matriz de \(J_z(J_z+\hbar)(J_z-\hbar)\) y de \(J_x(J_x+\hbar)(J_x-\hbar)\) en la base \(\left\{\left|{j=1,m}\right\rangle\right\}\) sin usar la representación matricial de \(J_x\).

    4. Muestre que en el caso de momento angular \(j=1\), vale que \[\RotationOp[(1)](\boldsymbol{\mathbf{\hat{y}}},\beta) = e^{-iJ_y\beta/\hbar} = 1 - i\left(\frac{J_y}{\hbar}\right) \sin\beta - \left(\frac{J_y}{\hbar}\right)^2 \left(1 - \cos\beta\right).\] Usando esto obtenga \[\RotationYMatrix[(j=1)](\beta) = \begin{pmatrix} \left(\frac{1}{2}\right)(1+\cos\beta) & -\left(\frac{1}{\sqrt{2}}\right)\sin\beta & \left(\frac{1}{2}\right)(1-\cos\beta) \\ \left(\frac{1}{\sqrt{2}}\right)\sin\beta & \cos\beta & -\left(\frac{1}{\sqrt{2}}\right)\sin\beta \\ \left(\frac{1}{2}\right)(1-\cos\beta) & \left(\frac{1}{\sqrt{2}}\right)\sin\beta & \left(\frac{1}{2}\right)(1+\cos \beta) \end{pmatrix},\] donde \(\RotationYMatrix(\beta)\) es la representación matricial de \(\RotationOp(\boldsymbol{\mathbf{\hat{y}}},\beta)\) en la base de autoestados de \(J_z\).

    [exc:spin1basics]

  7. Considere un sistema con \(j=1\) que se encuentra en el estado \(\left|{\psi}\right\rangle\) dado por \[\left|{\psi}\right\rangle = \frac{1}{\sqrt{2}}\left(\left|{j = {1}, m = {1}}\right\rangle - \left|{j = {1}, m = {-1}}\right\rangle\right).\]

    1. Si se mide \(L_x\) sobre \(\left|{\psi}\right\rangle\), ¿qué valores pueden obtenerse y con qué probabilidades? Repita el cálculo si se mide \(L_y\).

    2. Suponga que sobre el estado \(\left|{\psi}\right\rangle\) se mide \(L_z\) y se obtiene \(\hbar\), e inmediatamente después se mide \(L_y\). ¿Qué valores pueden obtenerse y con qué probabilidades?

  8. Dado un conjunto de tres operadores, \(\left\{A_1, A_2, A_3\right\}\), ¿cuál es el significado de la ecuación \(U^{-1} A_k U = \sum_{l} R_{kl} A_l\), donde \(R_{kl}\) es una matriz de rotación? A partir de esta ecuación, muestre que los elementos de matriz \(\left\langle{m}\right|A_k\left|{n}\right\rangle\) se transforman como vectores ante la transformación \(U\).

  9. Un autoestado de momento angular \(\left|{j,j}\right\rangle\) se rota en un ángulo infinitesimal \(\epsilon\) alrededor del eje \(\boldsymbol{\mathbf{\hat{y}}}\). Sin usar explícitamente la forma de la matriz \(d_{m'm}^{(j)}\), obtenga una expresión para la probabilidad de que el nuevo estado rotado se encuentre en el estado original, hasta términos de orden \(\epsilon^2\).

Momento Angular Orbital

  1. Construya los armónicos esféricos \(Y^{m}_{1}\). Para ello, resuelva primero \(L_+Y^{1}_{1} = 0\) (usando \(L_+\) en la representación \(r\)) y luego aplique el operador \(L_-\) a \(Y^{1}_{1}\) (previamente normalizado) para hallar los otros dos restantes. Usando los resultados de [exc:spin1basics], escriba la combinación lineal de los armónicos esféricos \(\left\{Y^{m}_{1}\right\}\) que es autoestado de \(L_y\) con autovalor \(\hbar\). Verifique su resultado aplicándole \(L_y\) en la representación \(r\).

  2. Suponga que fuera posible un valor semi-entero de \(l\) para el impulso angular orbital, por ejemplo \(l = 1/2\). A partir de \[L_+\,Y^{1/2}_{1/2}(\theta,\phi) = 0,\] podemos deducir \[Y^{1/2}_{1/2}(\theta,\phi) \propto e^{i\phi/2}\sqrt{\sin\theta}.\] Verifique esta afirmación. Intente construir entonces \(Y^{-1/2}_{1/2}(\theta,\phi)\) de dos maneras diferentes,

    1. aplicando \(L_{-}\) a \(Y^{1/2}_{1/2}(\theta,\phi)\),

    2. usando que \(L_{-}Y^{-1/2}_{1/2}(\theta,\phi) = 0\).

    Muestre que los dos procedimientos llevan a resultados contradictorios (esto da un argumento en contra de valores semi-enteros de \(l\)).

  3. Considere un autoestado de impulso angular orbital \(\left|{l = {2}, m = {0}}\right\rangle\). Suponga que este estado es rotado en un ángulo \(\beta\) alrededor del eje \(\boldsymbol{\mathbf{\hat{y}}}\). Encuentre la probabilidad de medir \(m=0\), \(\pm 1\), y \(\pm 2\) en el nuevo estado.

  4. La función de onda de una partícula sujeta a un potencial esféricamente simétrico \(V(r)\) está dada por \[\Psi(x,y,z) = (x + y + 3z)f(r),\] con \(f(r)\) alguna función de \(r = \sqrt{x^2 + y^2 + z^2}\).

    1. ¿Es \(\Psi\) autofunción de \(L^2\)? Si es así, ¿cuál es el valor de \(l\)? Si no es así, ¿cuáles son los posibles valores de \(l\) que pueden ser obtenidos cuando se mide \(L^2\)?

    2. ¿Cuáles son las probabilidades de hallar a la partícula en los distintos estados con \(m\) definido?

    3. Suponga que se sabe de alguna manera que \(\Psi(x,y,z)\) es una autofunción de energía con autovalor \(E\). Indique cómo puede hallarse \(V(r)\).

  5. Usando coordenadas esféricas, obtenga una expresión para la corriente de probabilidad \(\boldsymbol{\mathbf{j}}\) para el estado fundamental y los excitados del átomo de hidrógeno. Muestre en particular que, para los estados con \(m \neq 0\), existe un flujo toroidal en el sentido de que \(\boldsymbol{\mathbf{j}}\) está en la dirección de \(\phi\) creciente o decreciente dependiendo del signo de \(m\).

  6. Considere el Hamiltoniano de un rotor rígido, \[H = \frac{1}{2} \left(\frac{L_1^2}{I_1} + \frac{L_2^2}{I_2} + \frac{L_3^2}{I_3}\right),\] donde \(\boldsymbol{\mathbf{L}}\) es el impulso angular en el sistema de coordenadas fijo al cuerpo. A partir de esta expresión obtenga la ecuación de movimiento de Heisenberg para \(\boldsymbol{\mathbf{L}}\) y luego halle las ecuaciones de movimiento de Euler en el límite correspondiente.