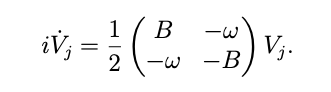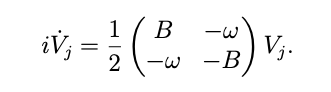
Una aclaración sobre el único problema de la guía 6, ítem (e). La base ortonormal de autoestados instantáneos de H está definida unívocamente… Salvo por una fase para cada uno de sus vectores. La ecuación tipo Schrödinger que aparece en este ítem (es decir, la ecuación que encabeza este post) se obtiene usando el resultado que les di en las slides de la guía 5 para los autoestados de la proyección del spin en una dirección cualquiera. Si ustedes usan una base que difiera de ésta por una fase dependiente del tiempo (cosa que tienen todo el derecho del mundo a hacer), entonces la ecuación tipo Schrödinger a la que van a llegar va a tener un hamiltoniano distinto. Y el resultado al que van a llegar para V_{++} va a diferir del que aparece en la guía por una fase, que va a ser precisamente (menos) la fase que relaciona la base que eligieron con la de las slides de la guía 5. En todo caso, como debe ser, esa fase no tiene ninguna relevancia física, porque en el cálculo de las probabilidades del trabajo sólo entra el módulo de los elementos de la matriz V. Así que, elijan la fase que elijan para los autoestados instantáneos del hamiltoniano, deben llegar al mismo resultado para las probabilidades del trabajo.
Por otra parte, en la pestaña Práctica hemos agregado una breve guía que hizo Juanma sobre WolframAlpha, donde les explica cómo calcular autovectores y autovalores de una matriz, resolver ecuaciones diferenciales, etc con esa herramienta, que es muy útil. En la guía sólo aparecen matrices 2×2 que son muy fáciles de diagonalizar (y deberían saber hacerlo!), pero está buenísimo tener la herramienta de WolframAlpha para chequear los resultados.