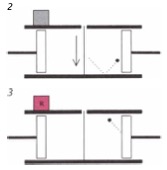
En la clase de ayer hablamos del demonio de Maxwell, y vimos que un ingrediente fundamental para reconciliar a ese ser con la segunda ley de la termodinámica es el principio de Landauer: el borrado de un bit de memoria a temperatura T conlleva la emisión de un calor mayor o igual a kT log 2 (acá tienen el artículo original de Landauer). La conexión entre el principio de Landauer y el demonio de Maxwell es obra de Charles Bennett, que escribió este artículo de divulgación sobre el tema en Scientific American que recomiendo leer, es muy claro y ameno. En clase también discutimos que el principio de Landauer por sí solo no es suficiente para reconciliar al demonio con la segunda ley. Hay que asumir además que el demonio (la memoria en el ejemplo de la máquina de Szilard) no absorbe calor en el proceso de medida, es decir, en el paso de 2 a 3 de la figura.
Y en ese proceso la entropía de la memoria aumenta (pasa de 0 a k log 2), así que, en principio, la segunda ley le da margen para absorber calor. En clase comenté por arriba un argumento para descartar esa posibilidad, y quiero aprovechar este espacio para dar algo más de detalle sobre ese argumento. La clave es que, en el proceso de medida, la memoria (m) se correlaciona con la máquina (M), y en consecuencia la entropía del sistema memoria + máquina, que en general es S(mM) = S(m)+S(M|m), no es simplemente suma de entropías como suele pasar en termodinámica. La segunda ley para el sistema mM nos dice que el calor absorbido Q cumple
Q/T ≤ ΔS(mM) = ΔS(m) + ΔS(M|m).
En el proceso de medida tenemos ΔS(m) = k log 2. Cuánto vale ΔS(M|m)? Inicialmente, conocer el estado de la memoria no nos dice nada sobre el estado del gas; en particular, el gas podría estar en cualquier mitad de la caja. En cambio, después de la medida conocer el estado de la memoria sí nos dice algo sobre el estado del gas: nos dice en qué mitad está. Por lo tanto, ΔS(M|m) = -k log 2, así que el calor absorbido en el proceso de medida cumple
Q/T ≤ 0,
como queríamos ver. Esto está bien explicado en las secciones 9.1 y 9.2 del libro An introduction to stochastic thermodynamics, de Naoto Shiraishi (es uno de los libros de la bibliografía del curso).
Un último comentario. Fíjense que, en los argumentos que usamos para reconciliar al demonio con la segunda ley, usamos la segunda ley. Ésa es una crítica que a veces se le hace a este tipo de argumentos. Pero para mí eso no es un problema. Estamos haciendo un test de consistencia, viendo si la aplicación de la segunda ley en distintas fases de un experimento imaginario nos lleva a una contradicción con esa misma ley.