El método de separación de variables, los armónicos esféricos y las expansiones multipolares que vemos en clase tienen aplicaciones en física que van mucho más allá de la electroestática y la magnetoestática. Y los armónicos esféricos no aparecen solo en estas áreas de la física o en la solución del átomo de hidrógeno. Como forman una base completa, se usan para representar formas y deformaciones de la simetría esférica en forma unívoca en muchos problemas (aún si los problemas no son lineales).

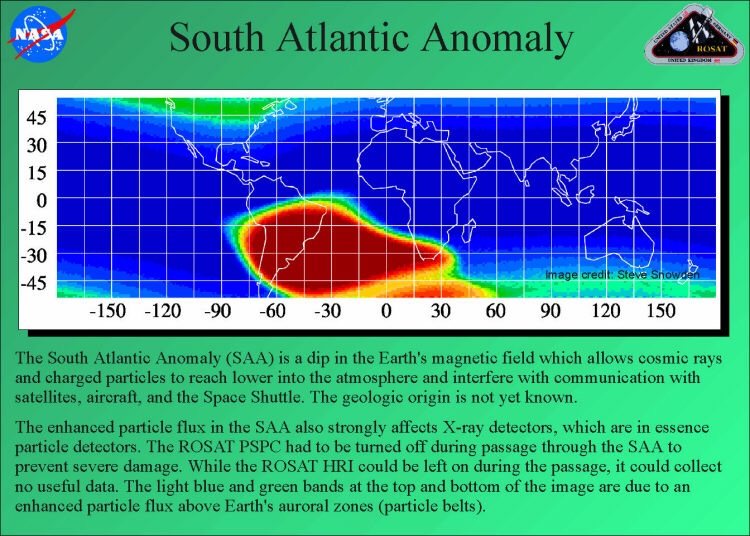
Por ejemplo, el campo magnético de la Tierra es mayormente dipolar. Pero el campo magnético tiene anomalías, regiones en la superficie de la Tierra en las que el campo magnético es menos intenso que la intensidad que correspondería al dipolo. Obviamente nuestra región tenía que estar en una anomalía, y una de las anomalías más conocidas y estudiadas es justamente la anomalía del Atlántico sur:

Los armónicos esféricos se usan para caracterizar esta anomalía (y también para caracterizar la “forma” de los campos magnéticos de otros planetas). Los que quieran leer más sobre esto pueden ver este paper sobre la anomalía del Atlántico Sur.

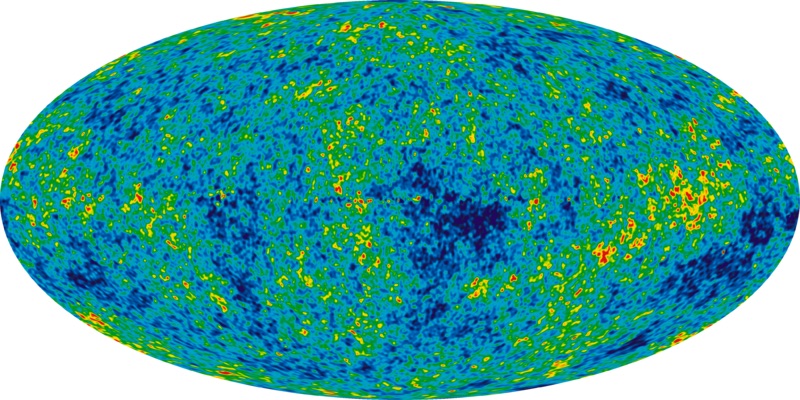
La anisotropía en la radiación cósmica de fondo (radiación electromagnética de cuerpo negro que fue emitida en el momento en que se formaron los primeros átomos en el universo, y que llega a nosotros proveniente de todas las direcciones) también se cuantifica usando armónicos esféricos. La radiación cósmica de fondo es aproximadamente isótropa. Pero si se resta el valor medio a la radiación, la proyección de las fluctuaciones de la amplitud de la radiación que nos llega de diferentes regiones del firmamento se ve así:

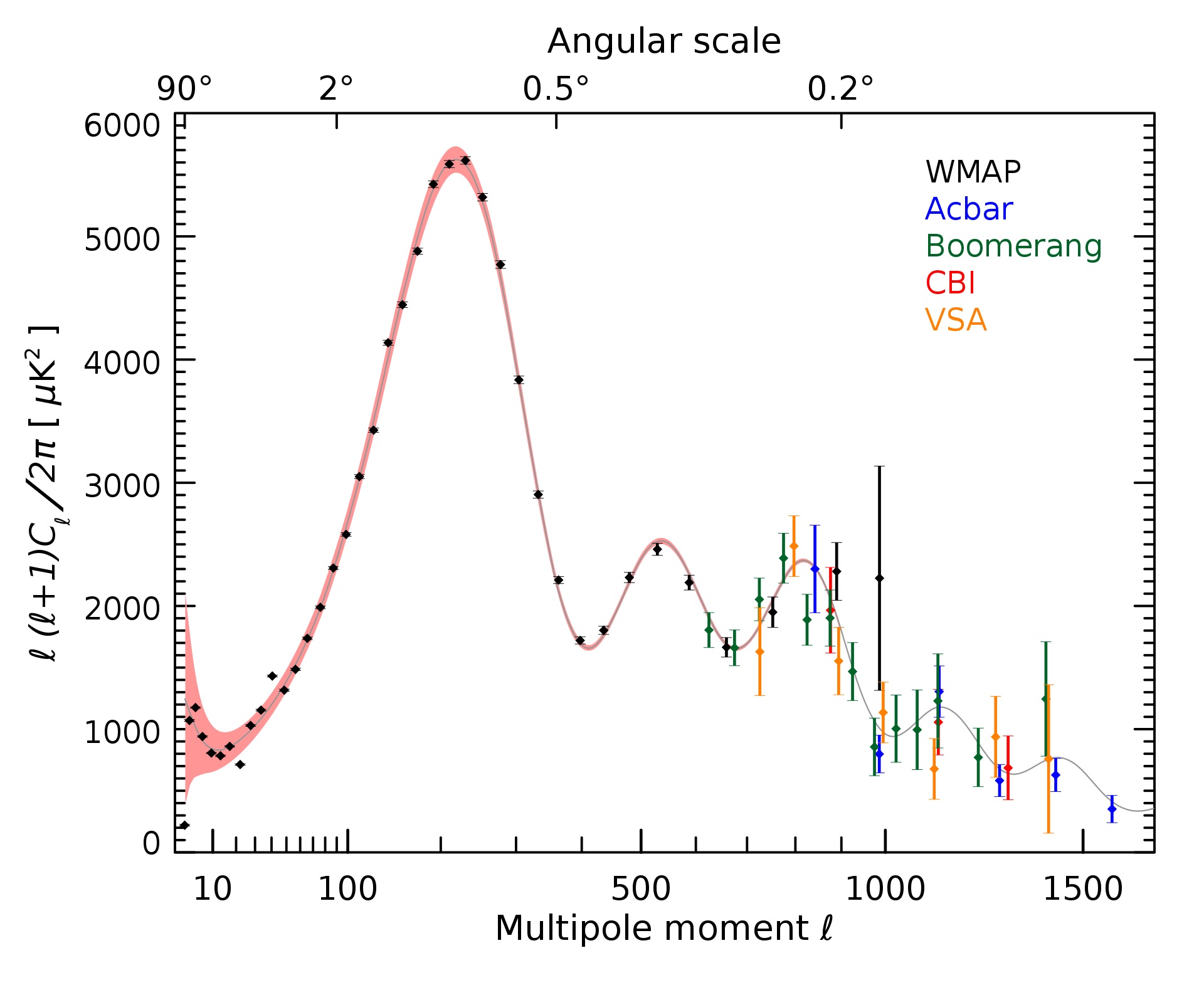
Lo que muestra esta imagen son las variaciones alrededor de la temperatura media asociada a la radiación de cuerpo negro que recibimos (el valor medio de la temperatura es de 2.725 grados Kelvin). Las regiones azules y rojas están, respectivamente, 0.0002 grados Kelvin a mayor o a menor temperatura que el valor medio. ¿Cómo podemos caracterizar estas fluctuaciones y extraer información cuantitativa sobre su anisotropía? Proyectando sus amplitudes en la base de armónicos esféricos. La figura a continuación muestra el espectro de la radiación cósmica de fondo en términos del momento multipolar l. Es decir, la amplitud de cada modo cuando la radiación cósmica de fondo se proyecta en la base de armónicos esféricos Y_lm, como muestra este gráfico tomado de Wikipedia:

¿Cómo leemos este gráfico? Si tuviéramos toda la amplitud de la señal de la radiación cósmica de fondo en el armónico esférico Y₀₀, entonces la radiación cósmica de fondo sería perfectamente isótropa, pues el armónico esférico con l = m = 0 tiene la misma amplitud en todas las direcciones. De hecho, la mayoría de la potencia en la radiación cósmica de fondo está en ese armónico esférico, así que para mirar la anisotropía ese modo se remueve (se resta). Por otro lado, tener picos en el resto de la señal en armónicos esféricos con l ≈ 200, 550 y 800 nos dice que tenemos variaciones con aproximadamente ese número de ceros en la coordenada θ (y probablemente también en Φ), o equivalentemente, que la radiación cósmica de fondo fluctúa con mayor amplitud con períodos que corresponden a ángulos subtendidos de aproximadamente 1, 0.4 y 0.2 grados. Claramente la señal no se limita solo a esos armónicos esféricos y tiene contribuciones de otros modos. Pero podemos imaginar cómo la superposición de estos modos reconstruye la señal mirando la siguiente figura, que muestra la parte real del armónico esférico con l = m = 1, del armónico esférico con l = 10 y m = 5, y la parte real de una superposición de solo 5 armónicos esféricos con valores de l y m entre 1 y 40 con fases al azar:

El espectro de la radiación cósmica de fondo no se usa solamente para describir la señal. Los picos en el espectro (el valor de l en el que ocurren, y su amplitud y forma) tienen información física. Como la radiación cósmica de fondo se generó en una etapa temprana del universo, se puede usar esta información para estimar parámetros importantes en cosmología, como la curvatura media de nuestro universo, o la densidad media de masa y energía en el universo. De esta forma sabemos que el universo es, en buena medida, plano.

Los armónicos esféricos también se usan para estudiar la emisión de ondas gravitatorias por la colisión de dos agujeros negros. Las fuentes (los dos agujeros negros) ocupan una región acotada del espacio, y emiten ondas que se pueden describir con una expansión multipolar en términos de los armónicos esféricos. Los que quieran tener una idea de cómo se hace esto pueden ver este documento técnico.

Para los que tengan más interés en estos últimos temas, en el Departamento de Física Gastón Giribet (@GastonGiribet) y el grupo de física teórica de altas energías (en el que también está Emilio Rubín de Celis o @EmiRubindeCelis, nuestro Jefe de Trabajos Prácticos) trabajan en problemas relacionados con los agujeros negros (entre otros grupos trabajando en temas afines en el Departamento).

Por suerte Sting no sabe expresar formas y deformaciones en términos de armónicos esféricos, y en lugar de hacer proyecciones en los elementos de esta base, escribe canciones para describir la forma de su corazón.

“Sun is shinin’ in the sky
There ain’t a cloud in sight
It’s stopped rainin’ everybody’s in the play
And don’t you know
It’s a beautiful new day, hey hey.“

Electric Light Orchestra, Mr. Blue Sky (1977).

Llegó la primavera y el cielo cambiará de a poco la tonalidad de su color azul, por un efecto electromagnético que veremos más adelante en el curso. Pero antes de explicar efectos tan complicados, el electromagnetismo tuvo su primer triunfo al asociar, en parte, los experimentos con cables y baterías de Faraday y de Ampère con lo que ven nuestros ojos: la luz y los colores.

Uno de los primeros logros de la teoría electromagnética de Maxwell fue identificar correctamente a la luz como radiación electromagnética. En uno de sus primeros papers sobre esta teoría, al reconocer que sus ecuaciones tenían soluciones en forma de ondas que se propagan a la velocidad de la luz, Maxwell hipotetizó que tal vez la luz fuera, simplemente, radiación electromagnética (aunque Faraday ya había jugado con esta idea al notar en sus experimentos que con un campo magnético podía modificar la polarización de la luz). La diferencia entre las ondas de radio (que se descubrirían al poco tiempo) y la luz es simplemente la región del espectro electromagnético que las diferentes ondas ocupan.

El espectro electromagnético visible es el que pueden ver nuestros ojos, y asociamos un color a cada longitud de onda:

Pero, ¿qué es el color azul? ¿Es simplemente una onda electromagnética con una longitud de onda cercana a los 460 nm? ¿Qué es el color rojo? ¿Y qué es el color rosa de aquella cosa que llamamos rosa?

“Si (como afirma el griego en el Cratilo)
el nombre es arquetipo de la cosa
en las letras de ‘rosa’ está la rosa
y todo el Nilo en la palabra ‘Nilo’.“

Jorge Luis Borges, El gólem (1958)

Estas preguntas no son retóricas, ni filosóficas, ni propias de Umberto Eco. Porque aunque como mencioné previamente el color azul del cielo se debe al electromagnetismo, la percepción del color azul no se limita simplemente a que nuestros ojos detecten una onda electromagnética en los 460 nm. Al menos en este caso, en las letras de la palabra ‘azul’ no está el azul. La percepción de los colores es increíblemente complicada e involucra al electromagnetismo, a la fisiología del ojo, y a las neurociencias.

Comencemos por algo sencillo. Nuestros ojos tienen dos tipos de células diferentes que son sensibles a la radiación electromagnética en el espectro visible: los bastones y los conos. La longitud de onda dominante en la luz determina el matiz (“hue“) que percibimos. Pero el matiz  (o la longitud de onda) no alcanza para determinar unívocamente el color que vemos.

Los bastones y los conos no tienen una sensitividad uniforme en todo el espectro. Los bastones son más sensibles a la luz y funcionan aún en ambientes con iluminación baja, pero tienen poca sensibilidad a las diferentes longitudes de onda. Por otro lado los conos son menos sensibles a la luz, pero tienen un mayor rango de sensibilidad a las diferentes longitudes de onda. Ellos son los responsables de que veamos en colores. Hay tres tipos de conos (básicamente, tres detectores que miden ondas en diferentes regiones del espectro). Dos tipos de estos conos tienen mayor sensibilidad entres los 520 y los 590 nm. Observen la imagen previa del espectro electromagnético: probablemente el color verde les parezca más intenso. Esto tiene que ver con la diferente sensibilidad de los conos a las diferentes longitudes de onda. La diferente sensibilidad a la luz de los conos y los bastones también hace que nuestra percepción de los colores cambie de acuerdo a la iluminación, o entre el mediodía y el atardecer. Un matiz rojo (es decir, con longitud de onda dominante de 620 nm) puede parecernos marrón de acuerdo a la iluminación. El ángulo en el que incide la luz sobre un material, y el espectro emitido por la fuente, también afecta nuestra percepción del color. Así, el color que percibimos depende no solo del matiz, sino también de la iluminación (y del brillo de la superficie entre otros detalles). Dado un espectro electromagnético en el rango visible, reconstruir un “color” a partir del mismo no es tarea fácil, y requiere tener en cuenta todas estas variables.

Como si esto no fuera suficiente, nuestro cerebro debe procesar la información proveniente de los bastones y los conos. Aunque el procesamiento de la información ocurre mayormente en la corteza visual, hoy se sabe que la información pasa antes por otras regiones cercanas del cerebro. Y la percepción de los colores se vuelve subjetiva, variando de un sujeto a otro. Recuerden todo esto cuando estén tentados en pensar que los colores que percibimos están simplemente definidos por la longitud de onda electromagnética dominante. Y los que tengan interés en temas más amplios de física y conciencia pueden mirar la página del grupo de neurociencias dirigido por Enzo Tagliazucchi (@Etagliazucchi) en el Departamento de Física.

Y finalmente, si se preguntan de dónde les suena Mr. Blue Sky, la canción de Electric Light Orchestra que dió inicio a este posteo en el que nos preguntamos qué es el color azul, probablemente sea de la apertura de Guardianes de la Galaxia Vol. 2, la película dirigida por James Gunn que les recomiendo para el fin de semana:

El 30 de octubre de 1938, Orson Welles, quizás el mejor director de cine de todos los tiempos (quien dirigió entre otras películas a Citizen Kane, una enciclopedia sobre cómo dirigir una película), hizo en la radio una versión teatralizada de “La guerra de los mundos“, la novela de ciencia ficción de H.G. Wells. En la novela marcianos invaden la Tierra y e inician una guerra contra la humanidad a escala global. Considerando las recientes observaciones de fosfano en Venus la temática de la novela de Wells es muy actual, aunque probablemente en este momento deberíamos estar saludando, en lugar de a los marcianos, a nuestros nuevos señores venusinos:

Orson Welles (cuya voz privilegiada pueden escuchar en el primer video) presentó la novela en la radio como un programa de noticias. En lugar de narrar la novela con la voz de otros actores leyendo algún diálogo, Welles pasó música (que interrumpió para presentar supuestas noticias urgentes sobre explosiones observadas en Marte), entrevistó actores en roles de científicos, y cambió las fechas y lugares de la novela para que la llegada de los marcianos ocurriese ese mismo día y en lugares de la costa este de los Estados Unidos. Y aunque al inicio del programa se presenta claramente a la transmisión como “Orson Welles and The Mercury Theater on the Air in ‘The War of the Worlds’”, varios desprevenidos que escucharon la transmisión ya comenzada pensaron que realmente correspondía a un programa de noticias, y que los marcianos habían invadido la Tierra. Esto catapultó a Orson Welles a la fama, y generó sucesos de histeria colectiva que se han vuelto famosos (aunque la gravedad de los sucesos probablemente haya sido exagerada en los días siguientes por los diarios).

La guerra imaginaria de Orson Welles tuvo un preludio muy real 60 años antes, en una guerra para desarrollar aplicaciones de la teoría electromagnética sin las cuales Welles no hubiera podido emitir su programa de radio (o, al menos, nadie hubiera podido escucharlo). Los principales actores en este enfrentamiento fueron Thomas Edison, Nikola Tesla, y George Westinghouse. Y la guerra se conoce hoy como la guerra de las corrientes (como título, no tiene nada que envidiarle a “La guerra de los mundos”).

Como vimos en un post anterior, Faraday inventó el primer generador eléctrico usando el fenómeno de inducción que había descubierto en sus experimentos. Hacia fines del siglo XIX Tesla inventó un generador de corriente alterna (AC) más práctico (aunque otros en la misma época inventaron generadores aún más prácticos), y más tarde inventaría un motor de corriente alterna similar a los que usamos hoy. Tesla, que en ese momento trabajaba en la compañía eléctrica de Edison, intentó convencer a Edison de la conveniencia de usar corriente alterna en las casas. Pero por razones monetarias (Edison ya había invertido mucho dinero en un sistema de corriente continua, o DC) Edison rechazó esa idea. Tesla terminó siendo contratado por Westinghouse, un ingeniero dueño de la compañía eléctrica Westinghouse, quién compró además las patentes de Tesla. Con esas patentes, generadores de la empresa Siemens, y un transformador inventado en Europa, Westinghouse trató de vender su sistema de tendido eléctrico para los hogares con corriente alterna. Obviamente el inicio de la batalla entre estos dos sistemas merece ser musicalizado por AC/DC:

Ambas empresas iniciaron largas campañas para vender sus sistemas a las ciudades que comenzaban a instalar tendidos eléctricos para los hogares. Desde el punto de vista de la eficiencia, el sistema AC era muy superior al sistema DC, y lentamente fue ganando preponderancia. En 1888 la compañía de Edison decidió que era el momento de iniciar campañas mediáticas más directas (y menos honestas) contra la corriente continua. Acusaron a la corriente continua de ser más peligrosa, y hasta pagaron una especie de circo itinerante que recorría ciudades electrocutando animales con corriente continua para mostrar sus riesgos (la invención de la silla eléctrica fue un subproducto de esta guerra). A pesar de la campaña de Edison y su empresa, la mayor eficiencia del sistema de corriente alterna terminó ganando la pelea y para 1890 la mayoría de las empresas de distribución eléctrica usaban este sistema (que usamos hoy en todas nuestras casas).

Cerrando el ciclo de comics y el electromagnetismo, los que quieran leer más sobre esta historia pueden mirar un cómic corto (y un poco infantil en la visión de los roles de cada uno de los actores de esta batalla) realizado por la American Physical Society:

• Nikola Tesla and the electric fair.

En 2010, Scott Pilgrim fue adaptado al cine (la película está disponible en Netflix). Si bien fue un fracaso en taquilla, y el personaje de Scott en la película por momentos puede ser irritante, la película captura muy bien la estética del cómic original y más tarde se volvió una película de culto. Superman, Capitán América y Capitana Marvel aparecen en la película (¡no en esos roles!). Y el director, Edgar Wright, dirigió varias películas interesantes, entre las que recomiendo dos películas en las que actúa el dúo humorístico británico formado por Simon Pegg y Nick Frost: Shaun of the dead y Hot Fuzz (como verán, esta materia también da un servicio, y les deja recomendaciones de películas para el fin de semana).

Con la película de Scott Pilgrim podemos adentrarnos en el round 3 (y último por el momento) de las batallas de Maxwell para defender las ecuaciones de sus sueños. Y esta batalla será contra la mecánica cuántica. Las cuatro leyes empíricas detrás de las ecuaciones de Maxwell (asociadas a los experimentos de Coulomb, Ampère y Faraday, y a la inexistencia de monopolos magnéticos) son compatibles con observaciones y experimentos en escalas muy grandes y muy pequeñas. Por ejemplo, la ley de Coulomb es compatible con experimentos para separaciones entre cargas en distancias que van desde 10⁸ m hasta 10⁻¹⁶ m. En resumen, el comportamiento del mundo microscópico es, hasta donde hoy sabemos, compatible con las leyes detrás de las ecuaciones de Maxwell.

Sin embargo, el campo electromagnético clásico en las ecuaciones de Maxwell no está cuantizado. Pero eso no es un problema, porque las ecuaciones de Maxwell son las ecuaciones de onda para un fotón. Cuantizarlas cambia la interpretación física de los campos E y B, pero no agrega ni quita términos en las ecuaciones. La radiación de cuerpo negro, que corresponde a la emisión de fotones en equilibrio térmico por una fuente, satisface las ecuaciones de Maxwell tal como las vemos en esta materia.

La convivencia de Maxwell con la nueva física del siglo XX no fue lecho de rosas (para la nueva física). La ecuación de Schrödinger, como las ecuaciones de Newton, no es relativista. Es decir, la ecuación de Schrödinger es invariante de Galileo. Acoplar ciertos fenómenos cuánticos con el electromagnetismo no requirió modificar al electromagnetismo, sino modificar la mecánica cuántica para considerar el caso relativista. Nuevamente las ecuaciones de Maxwell resultaron victoriosas. Pero en la descripción cuántica-relativista las cosas se ponen difíciles. El número de partículas puede cambiar en el tiempo vía los procesos de creación y destrucción de pares: un fotón puede generar pares de partículas, siempre conservando la carga (como al crear un electrón y un positrón). La descripción de estos fenómenos es hoy descripta por la electrodinámica cuántica, que es la teoría que acopla correctamente al electromagnetismo y la materia en el caso cuántico-relativista. Esta teoría, por la que Sin-Itiro Tomonaga, Julian Schwinger y Richard Feynman ganaron el premio Nobel en 1965, es increíblemente precisa y compatible con los experimentos hasta el momento. Y algunas propiedades que conocemos del electromagnetismo clásico, como el principio de superposición, se pierden: el hecho de que el número de partículas pueda cambiar permite que un fotón interactúe con otro fotón. Pero esto no es el resultado de una corrección a las ecuaciones de Maxwell, sino del acoplamiento de las ecuaciones de Maxwell con la cuántica (y con la materia). Los que quieran aprender más sobre esto, qué mejor que hacerlo escuchando a uno de los creadores de la teoría:

En resumen, las ecuaciones de Maxwell no cambiaron a lo largo del siglo XX, aún durante la revolución de la mecánica cuántica. Las ecuaciones que hoy conocemos para los fenómenos electromagnéticos son las mismas que Maxwell escribió en 1861. Y no son una aproximación clásica que requiera correcciones en el caso cuántico. Para un solo fotón en vacío, las ecuaciones de Maxwell siguen siendo las ecuaciones de la física compatibles con las observaciones experimentales.

Aviso: Considerando el anuncio de último momento sobre el día del estudiante el 21 de septiembre, y el apretado cronograma de la materia, luego de las conversaciones que tuvimos en la última clase hemos decidido dictar clases por Zoom el lunes. Quienes no quieran o puedan conectarse pueden ver la clase grabada el día siguiente, y pueden enviar sus consultas al foro.

Scott Pilgrim es un cómic canadiense creado por Bryan Lee O’Malley (también hay una película, pero eso será tema de un próximo post). El comic sigue las aventuras de Scott, que luego de enamorarse perdidamente de Ramona Flowers, descubre que la relación con Ramona tiene duras condiciones: debe enfrentarse con sus siete ex diabólicos (por diversos motivos, este tipo de cosas siempre se descubren demasiado tarde). Por enfrentarse, me refiero a que debe ganar una pelea. Y cada uno de los ex de Ramona es alguien famoso, fuerte, o con superpoderes. El cómic, que explora entre otras cosas las consecuencias de las relaciones tóxicas, combina el estilo del cómic norteamericano con el del manga y los videojuegos (por ejemplo, la banda de rock de Scott Pilgrim se llama “Sex Bob-omb”, una referencia a los Bob-omb de Super Mario). Casualmente hace dos días (el 13 de septiembre) se cumplieron los 35 años del lanzamiento de Super Mario Bros.:

Como Scott Pilgrim, James Maxwell también descubrió que para escribir las ecuaciones de sus sueños debía enfrentarse a varios ex malvados de la física. Sus ecuaciones eran, y fueron, incompatibles con varias otras teorías. Maxwell no llegó a ver el final de varios de esos enfrentamientos, pero su teoría los ganó a todos. En más de un sentido sus ecuaciones son las primeras ecuaciones de la física contemporánea, que iniciaron (antes que la cuántica) una revolución que afectaría fuertemente a toda la física en la primera mitad del siglo XX. Y sus ecuaciones no cambiaron ni en un solo término, a pesar de todos los cambios que tuvo la física en ese período. Como Samwise Gamgee en El señor de los anillos, Maxwell tal vez sea el héroe anónimo de la física moderna, opacado por otros grandes nombres que se subieron a sus hombros para poder ver mas lejos.

El primer round de Maxwell contra los ex malvados (¡round 1!) fue nada más y nada menos que contra el mismísimo Isaac Newton. En 1861, las ecuaciones de Newton y su Principia Mathematica tenían 174 años sin que nadie se atreviese a discutir su validez. Pero la fuerza electromagnética tiene un problema. Para una carga puntual q que se mueve con velocidad v, la fuerza electromagnética en unidades cgs-Gaussianas está dada por la fuerza de Lorentz (donde c es la velocidad de la luz):

Las leyes de Newton nos dicen que dos observadores en sistemas inerciales que se mueven con velocidad constante uno respecto al otro deben medir la misma fuerza. Pero también según Newton, si un observador S’ se mueve con velocidad constante u respecto a nuestro sistema de referencia S, el observador S’ verá que la carga se mueve con una velocidad relativa v‘ = v - u. La igualdad de la fuerza para ambos observadores implica que si nosotros vemos campos eléctricos y magnéticos E y B, el observador S’ debe ver campos B‘ = B y E‘ = E – u x B/c. Sin embargo, las ecuaciones de Maxwell no son compatibles con esta transformación para los campos frente a un cambio en el sistema de referencia (¡prueben hacer la cuenta y verán que las ecuaciones cambian!). Así, o las ecuaciones de Newton están mal, o las ecuaciones de Maxwell están mal. Alguien iba a salir lastimado de este enfrentamiento.

Como sabemos, este round lo ganó Maxwell (¡Game over!). La teoría de la relatividad especial de Einstein modificó la mecánica clásica, e introdujo nuevas transformaciones frente a un cambio de sistema de referencia que preservan la invariancia de las ecuaciones de Maxwell. En 1905, las ecuaciones de Maxwell seguían siendo las mismas que las que Maxwell escribió en 1861. Las ecuaciones que fueron modificadas fueron las de la mecánica de Newton, no las del electromagnetismo. Más adelante en la materia veremos este problema, y su resolución, en detalle.

¡Round 2!: Hace unos días Juan Pablo Pinasco (@jpinasco) del Departamento de Matemática me mandó un paper muy interesante, con una demostración de las ecuaciones de Maxwell que contó alguna vez Feynman (¿a modo de broma?), y que Freeman Dyson formalizó y puso por escrito:

• Feynman’s proof of the Maxwell equations.

Feynman parte de las ecuaciones de Newton y las relaciones de conmutación en cuántica, y obtiene dos de las ecuaciones de Maxwell (Dyson considera que las otras dos ecuaciones de Maxwell meramente definen las fuentes). Pero son las otras dos ecuaciones (y la conservación de la carga en particular) las que hacen imposible sostener la invariancia de Galileo en el electromagnetismo. Como Dyson mismo comenta (y otros autores en sus cartas al editor en el mismo archivo), el argumento de Feynman debe ser interpretado mas bien como una verificación de la consistencia de la física que conocemos. ¡Maxwell también gana este round!

Aprovecho para avisar que el Campus Virtual de Exactas tiene algunos problemas; esperamos que se resuelvan pronto para que puedan hacer todas sus consultas en los foros. Y para cerrar este primer posteo de los enfrentamientos de Maxwell con la física con una temática más ligera que la de los posteos previos del ciclo de cine de terror e historia del electromagnetismo (que puede haber impresionado a algunos), les dejo un video con una versión animada del cómic de Scott Pilgrim:

En esta última entrega de la serie de películas de terror (¡por el momento!), tenemos una de las mejores de películas de John Carpenter. “La cosa” (The thing, 1982) cuenta la historia de un grupo de investigadores encerrados en una base norteamericana en la Antártida, que debe enfrentarse a un parásito extraterrestre. El parásito no se puede destruir, y se transforma en el organismo que invade (y más tarde puede transformarse en otras cosas). Es un clásico del cine de terror y de la ciencia ficción, y una película de culto que pueden ver en Netflix. No solo la película es fuertemente recomendada para aprobar esta materia, sino que la temática general (con personas aisladas y encerradas, y tests de sangre para detectar un virus) es ideal para los tiempos que vivimos.

El concepto de que “nada se pierde, todo se transforma” se basa en la observación de la naturaleza. Tal vez el primero en ponerlo en estos términos fue Antoine Lavoisier, en el marco de sus experimentos en química. Pero en física hoy conocemos formalmente esta idea en la forma de leyes de conservación: ciertas cantidades en la naturaleza no cambian aún si un sistema aislado evoluciona en el tiempo. James Clerk Maxwell fue el primero en notar que las expresiones empíricas que se seguían de las observaciones experimentales de Coulomb, Ampère y Faraday no conservaban la carga eléctrica: la carga eléctrica según las ecuaciones del electromagnetismo de la época podía ser creada o destruida de la nada. Pero la evidencia experimental hasta ese momento indicaba que la producción de una carga positiva venía siempre acompañada por una carga negativa, es decir, que la carga total en un sistema aislado no puede cambiar (algo que se sigue verificando experimentalmente hasta el día de hoy). Maxwell entonces modificó las expresiones agregando el famoso término de la corriente de desplazamiento, de forma tal que las ecuaciones del electromagnetismo conserven la carga eléctrica total:

Como vimos en clase, de izquierda a derecha y de arriba hacia abajo, estás ecuaciones se obtienen respectivamente de la fuerza de Coulomb, de los experimentos de Faraday (que Maxwell escribió en esta forma), de la no observación de cargas magnéticas, y de las observaciones de Ampère. El último término en esta ecuación fue agregado por Maxwell para conservar la carga. Y aquí aparece la genial Emmy Noether:

Uno de los teoremas más importantes en la física teórica moderna, el teorema de Noether, nos dice que cada ley de conservación está asociada a una simetría. ¿A qué simetría se asocia la conservación de la carga? La conservación de la carga está asociada a la simetría de gauge del electromagnetismo. Sabemos que, por ejemplo, podemos sumarle una constante C a cualquier potencial φ, y obtener el mismo campo eléctrico

Es decir, podemos elegir arbitrariamente el cero del potencial. Y también sabemos que el trabajo necesario para desplazar una carga q entre dos puntos 1 y 2 con diferentes valores del potencial es W = q(φ₂ – φ₁). Luego, si fuera posible crear cargas de la nada, el trabajo necesario para crear una carga en un punto cualquiera debería ser qφ. Pero esto nos permitiría determinar el valor absoluto del potencial electrostático φ (¡y determinar en forma absoluta el cero del potencial!) simplemente midiendo el trabajo necesario para crear la carga q. Así, la conservación de la carga y la libertad de gauge del electromagnetismo están relacionadas: si la carga total no se conserva, podemos determinar en forma única el cero de los potenciales.

La conservación de la carga implica que no podemos cambiar la cantidad total de carga en el universo. Pero esto no implica que el universo tenga una carga eléctrica total igual a cero. Podría haberse originado con un desbalance de carga (por ejemplo, más cargas positivas que negativas), y por la conservación de la carga, el desbalance total de carga hoy debería ser el mismo que al inicio del universo. Pero toda la evidencia observacional hasta el momento indica que el universo es eléctricamente neutro. Por ejemplo, un desbalance de carga generaría campos eléctricos que impondrían una dirección privilegiada en el espacio y una anisotropía en la radiación cósmica de fondo, o una anisotropía en los rayos cósmicos que llegan a la Tierra. Nada de eso se observa. Si hay un desbalance de carga en el universo, debe ser muy pequeño.

No dejen de ver este y este anuncio importante sobre la práctica, y en la página de la teórica ya pueden encontrar los apuntes para la próxima clase y el video de la clase del miércoles.

La película es “La novia de Frankestein” (1935), y el monstruo es protagonizado por el mítico Boris Karloff y Elsa Lanchester. En la novela original de Mary Shelley el monstruo también pide que le construyan una pareja, o en caso contrario amenaza con matar a toda la familia del profesor Frankestein (un caso interesante y bastante literal de “publish or perish“). Pero el profesor Frankestein se niega a dar vida a otro monstruo. Sin embargo, en esta secuela a una película original sobre Frankestein y su monstruo de 1931, el profesor hace lugar al pedido. La vida se insufla, tanto el monstruo como en su novia, con electricidad. La imagen de la novia de Frankestein (Elsa Lanchester), con su pelo en forma cónica y la onda blanca en forma de rayo a los costados, se ha vuelto una imagen icónica en la cultura popular. Todas las películas recientes sobre la historia de Frankestein no están a la altura de estas primeras películas: esta imagen, como la imagen clásica de Karloff en el papel del monstruo, con la frente amplia y los electrodos a los costados del cuello, se han vuelto imágenes de culto.

Mary Shelley escribió Frankestein en 1818. A fines del siglo XVIII Galvani y Volta hicieron una serie de experimentos en los que mostraron que hacer circular electricidad por la pata de una rana muerta contraía sus músculos, y la pata se movía. Los experimentos tuvieron un impacto importante en la cultura popular de la época e inspiraron a Mary Shelley. El descubrimiento tuvo también aplicaciones médicas en la electroterapia moderna, en el marcapasos, y el desfibrilador.

Los experimentos de Galvani y Volta forman parte de la serie de experimentos que entre los siglos XVIII y XIX establecieron las leyes fundamentales del electromagnetismo tal como hoy las conocemos. Y la serie de experimentos más influyentes fue realizada por Couloumb, Ampère, y Faraday. Couloumb usó materiales cargados eléctricamente y una balanza de torsión para determinar que la fuerza electrostática de atracción o repulsión entre las cargas es proporcional al producto de las cargas e inversamente proporcional a la distancia que las separa. Coulomb publicó tres trabajos con estos resultados experimentales a partir de 1785. La imagen de su balanza de torsión se muestra a continuación. Le permitió medir con mucha precisión la fuerza de atracción o de repulsión entre cargas, y poniendo las cargas a diferentes distancias (una sobre el brazo de la balanza de torsión, y desplazando libremente a la otra), mostrar que la fuerza decrecía con el cuadrado de la distancia que separaba a ambas cargas (básicamente, midiendo el ángulo en que se movía el brazo de la balanza):

Ampère hizo experimentos con cables, corrientes, y brújulas, continuando experimentos que fueron realizados primero por Ørsted en 1820. Ampère rápidamente se dio cuenta que la aguja de una brújula se alinea a lo largo de círculos concéntricos cuando la brújula me mueve en el plano perpendicular a un cable recto por el que circula una corriente. Y realizó experimentos para medir la fuerza entre dos cables rectos por los que circulan diferentes corrientes. Pero determinar una expresión para la fuerza magnetostática es mucho más difícil que en el caso electrostático considerado por Couloumb. La fuerza cambia de acuerdo a cómo se alinean los cables y a la dirección en la que circulan las corrientes, y construir evidencia experimental confiable requiere muchos más experimentos, con muchas más configuraciones (y muchos más papers), que los tres papers publicados por Coulomb a fines del siglo XVIII. Para comprender esto basta comparar la expresión moderna de la fuerza de Coulomb con la de la fuerza magnetostática en la ley de Biot-Savart (1820), ambas en el sistema de unidades cgs-Gaussiano:

Mientras que la primera fuerza solo involucra dos magnitudes escalares (las cargas q₁ y q₂, respectivamente en posiciones r₁ y r₂), la segunda expresión involucra magnitudes vectoriales asociadas a las direcciones de las corrientes I₁ e I₂ a lo largo de dos cables, y las integrales sobre todo el recorrido de ambos cables.

Algo parecido ocurrió con los experimentos de Faraday. Y el caso de Faraday brinda además un ejemplo interesante de cómo se comunicaba la ciencia en el siglo XIX, y cómo se sigue comunicando hoy. Entre 1821 y 1832 Faraday hizo una gran cantidad de experimentos estudiando el fenómeno de inducción, creando el primer generador (un dínamo), e identificando con éxito la relación entre corriente y voltaje. En su serie de experimentos más importante, condensada en la ley de Faraday en las ecuaciones de Maxwell, usó dos cables aislados para mostrar que al variar en el tiempo la corriente que pasa por uno de los cables, otra corriente es inducida en el segundo cable. Uno de sus experimentos se veía aproximadamente así:

Las dos bobinas (A y B) están enrolladas alrededor de un mismo núcleo, pero aisladas entre si. La corriente en la bobina A se hace variar en el tiempo conectando y desconectando la batería que se encuentra a la derecha. Y el galvanómetro G, a la izquierda, se usa para detectar la corriente inducida en la bobina B al conectar y desconectar la bobina A. Este tipo de experimentos suele contarse como si fueran experimentos demostrativos. Pero para determinar expresiones empíricas para las fuerzas eléctrica, magnética, y electromotriz, fue necesario construir y publicar grandes cantidades de tablas. Solo en la revista Philosophical Transactions of the Royal Society, Faraday publicó más de 30 papers y reportes con diferentes configuraciones y mediciones de sus experimentos, la mayoría de ellos en una serie de trabajos numerados con el título “Experimental researches in electricity” (¡y los papers fueron refereados por pares!). Es decir, ya en 1832 Faraday comprendía la importancia de publicar sus resultados (aunque fueran preliminares) luego de ser evaluados por colegas, y de comunicar lo aprendido brindando explicaciones de los detalles, las limitaciones de sus experimentos, valores para cada una de sus mediciones, y estimaciones de los errores experimentales. Más allá de las discusiones contemporáneas sobre “publish or perish” y las prácticas actuales de ciertas editoriales científicas, el deseo por comunicar lo que uno descubre es atemporal, y la mayoría de los grandes físicos en la historia generaron gran cantidad de trabajos para sostener el diálogo con sus colegas, discutir, y aprender de los resultados de otros.

Los que quieran leer más sobre la historia temprana del electromagnéticos, y especialmente sobre los papers publicados por Faraday describiendo sus experimentos, pueden leer este paper reciente en Philosophical Transactions of the Royal Society:

• The birth of the electric machines