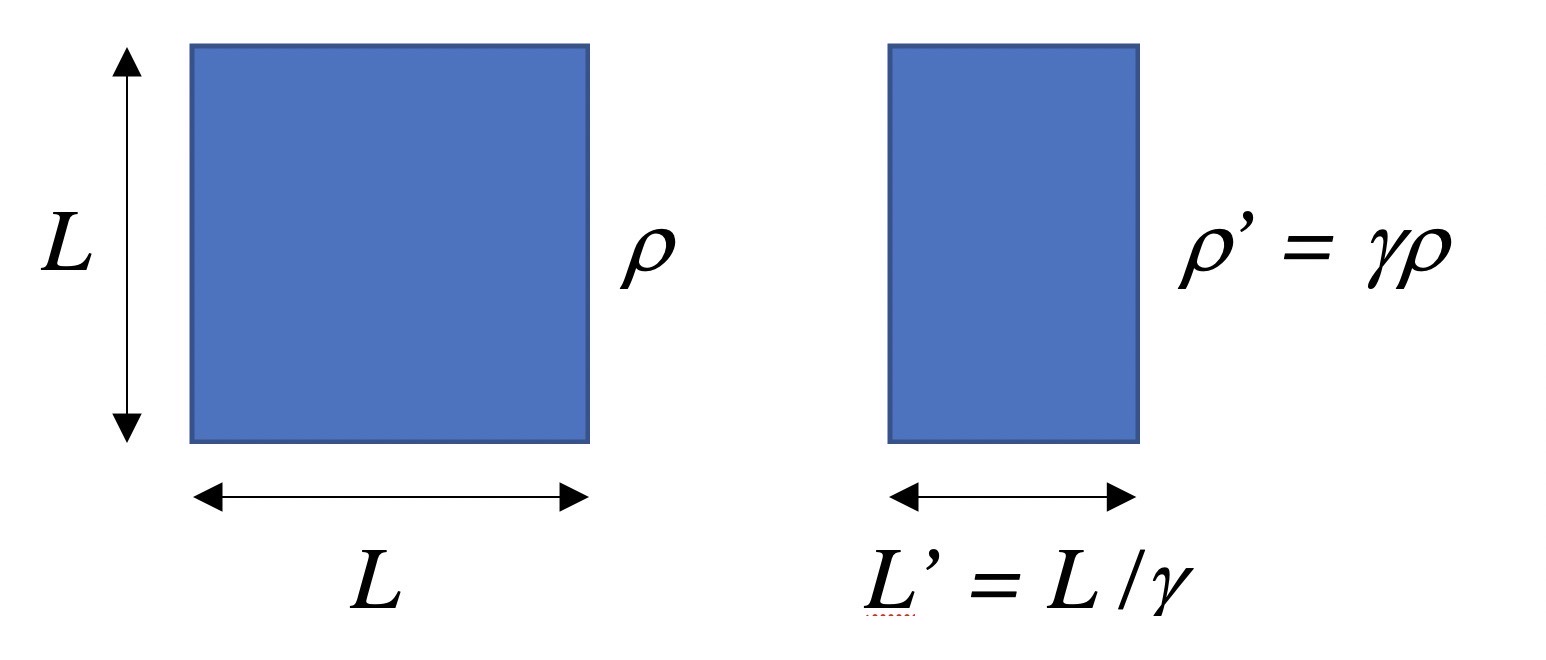En el video del posteo anterior en un momento Carl Sagan decía que Paolo experimentaba “something even stranger” (algo aún más extraño). Las propiedades contra-intuitivas de la relatividad especial han sido ampliamente usadas por la ciencia ficción, en muchos casos en forma laxa como en el uso de dimensiones extra y el concepto del “otro lado” en Stranger Things, en el viaje en el tiempo en Dark, o en la noción relativa de la simultaneidad en la novela Los desposeídos de Ursula K. Le Guin (una novela que explora muchos otros temas, como el anarquismo, el capitalismo, y el feminismo). Y algunos fenómenos en la relatividad especial realmente podrían motivar la frase de Alfonso VI al Cid: “Cosas tenedes, Cid, que farán fablar las piedras“.
En este último posteo en la serie sobre relatividad especial vamos a tocar un tema que puede parecer menos extraño, pero que sin embargo genera mucha confusión a la hora de estudiar el electromagnetismo: el de la invariancia de la carga eléctrica. La invariancia de la carga no debe confundirse con la conservación de la carga, y con el hecho de que la ecuación que expresa la conservación de la carga vale en todos los sistemas de referencia inerciales sin que cambie su forma.
La invariancia de la carga se basa en un hecho empírico sencillo: un átomo con carga total nula sigue teniendo carga total nula aunque el observador se encuentre en movimiento. Y los electrones tienen carga -e sin importar el sistema del referencia del observador. Para comprender mejor esto, consideremos la forma en la que se transforma la densidad de carga ρ cuando la mide un observador que se mueve en la dirección x con velocidad v respecto a nosotros. Para simplificar el argumento, asumamos que en nuestro sistema de referencia solo hay densidad de carga en reposo (con carga total Q) y la corriente es cero. El observador en movimiento entonces ve una densidad de carga y de corriente
Noten que el observador ve una densidad de carga ρ‘ > ρ. Pero el aumento en la densidad de carga no se debe a la aparición de la corriente jx‘. Este aumento en realidad se debe a que el observador en movimiento ve a la distribución de carga contraída por un factor 1/γ en la dirección x, debido a la contracción de Fitzgerald-Lorentz. Para simplificar aún más este argumento, pensemos que tenemos un cubo con lados con longitud en reposo L y con densidad de carga uniforme ρ, como se muestra en la siguiente figura a la izquierda. El observador en movimiento ve la distribución de carga que se muestra a la derecha (contraída espacialmente en la dirección en la que se mueve el observador, pero con la misma altura que mide el observador en reposo):
La carga total que ve cada observador, respectivamente Q y Q’, son el producto de las densidades de carga por el volumen. Y cumplen que Q = ρ L3, y Q’ = ρ‘ L’ L 2 = (γρ) (L/γ) L 2 = ρ L 3 = Q. Es decir, la carga total es la misma en ambos sistemas de referencia. El observador en movimiento ve una densidad de carga mayor simplemente porque observa que la carga ocupa un volumen menor, por el fenómeno de contracción espacial.
Quienes quieran pensar estas transformaciones en situaciones más complicadas, y verificar que la carga total efectivamente debe ser invariante frente a cambios de sistemas de referencia, pueden repasar la sección 13.6 de The Feynman Lectures on Physics, donde Feynman considera situaciones con cables, densidades de cargas y corrientes, y también se pregunta qué ocurre con la fuerza magnética que mide cada observador (todo este capítulo es muy recomendable):
Falta poco para que termine la materia. Así que no dejen de ver este importante anuncio para aquellos que tengan que recuperar la entrega de ejercicios, no hayan llegado a entregarlos a tiempo, o simplemente estén emocionalmente agotados. ¡A no bajar los brazos que ya termina el 2020, y pueden terminarlo con la fantástica noticia de haber aprobado la que tal vez sea la materia más larga de la carrera! Y no olviden que hoy es el último día para completar la encuesta obligatoria en la página de inscripciones.