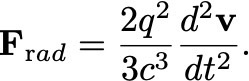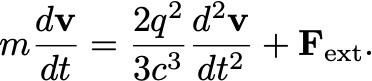Cuando hablamos de radiación, muchos piensan en peces con tres ojos o en Godzilla (Gojira). Godzilla es el más famoso de los kaiju (que quiere decir bestia extraña o bestia gigante en japonés). Y la primera aparición de este kaiju en la película de Ishirō Honda de 1954 dio inicio a una serie de películas en Japón y en Estados Unidos de calidad diversa, y vida a toda una familia de monstruos que quieren destruir (o proteger) a Tokio, entre los que se destacan Gamera, Rodan, Mothra, Anguirus, King Ghidorah y Mechagodzilla. Probablemente la mejor película reciente (¡recomendada por esta materia!) sobre kaijus y mechas sea Pacific Rim (2013), dirigida por Guillermo del Toro y que toma elementos de clásicos del animé como Neon Genesis Evangelion (ojo que me refiero a la primera película de la saga, no a la segunda). ¡Y sobre este tipo de radiación, también pueden leer sobre la vida de Marie Skłodowska Curie!

En términos generales, la radiación es la emisión de energía en forma de partículas u ondas. La radiación nuclear que da origen a la aparición de Godzilla está formada por partículas que son emitidas por el decaimiento de los núcleos atómicos, como partículas α (dos protones y dos neutrones), electrones o positrones, protones o neutrones. El decaimiento de un núcleo atómico también puede producir radiación electromagnética con longitud de onda muy pequeña, en la forma de fotones que en el contexto del estudio de la radiación núclear toman el nombre de partículas γ.

En esta materia hablaremos específicamente de radiación electromagnética en cualquier región del espectro electromagnético, que puede ser emitida no solo por decaimiento nuclear sino también por antenas (como la antena de un Wi-Fi o de una emisora de radio), o por cualquier fuente electromagnética variable o por cargas que se muevan en movimiento acelerado. De hecho, vivimos en un universo permeado por la radiación electromagnética. Y cuando miramos el firmamento, una fracción importante de la radiación electromagnética total que nos llega del espacio y de otras galaxias se debe al proceso de bremsstrahlung o frenado por radiación. Cualquier cambio en la velocidad de los electrones en el gas ionizado que forma el medio interestelar genera radiación electromagnética, y la energía que pierden los electrones de esta forma los frena. A su vez, la desaceleración por el frenado genera más radiación electromagnética, y así el proceso continúa. El resultado es radiación en longitudes de onda de rayos X que se puede observar con radiotelescopios (aunque no toda la radiación electromagnética que nos llega en estas longitudes de onda se debe a frenado por radiación):

Conocer el mecanismo de radiación electromagnética detrás de estas imágenes nos permite inferir propiedades de la fuente (como la densidad del gas en la galaxia, o su temperatura). Sin embargo, la descripción clásica del proceso de frenado por radiación no es sencilla y tiene varias limitaciones. La razón está relacionada con que describir el frenado por radiación requiere acoplar las ecuaciones de Maxwell con las ecuaciones de movimiento de las partículas, pero en el caso clásico las ecuaciones de Newton no son invariantes de Lorentz. Maxwell y Newton son como Godzilla y Mechagodzilla (que no se llevan bien entre sí).

Veamos brevemente cuál es el problema. A partir de la fórmula de Larmour para la potencia irradiada por una carga acelerada, y usando conservación de la energía (es decir, pidiendo que la potencia que se irradia sea igual al trabajo realizado para frenar a la partícula) podemos estimar la fuerza efectiva de frenado que siente una partícula acelerada con masa m y carga q como

Reemplazando esta fuerza en la ecuación de Newton, y permitiendo que actúen otras fuerzas externas sobre la partícula que representamos como F_ext, nos queda la siguiente ecuación:

El primer término de la derecha es la fuerza de rozamiento de Lorentz, y representa justamente a un rozamiento efectivo que aparece como resultado de la energía perdida por la partícula cargada por la emisión de radiación electromagnética. Para una partícula sin carga (q = 0) recuperamos la ecuación de Newton. Pero esta ecuación tiene un problema. En ausencia de fuerzas externas (F_ext = 0) admite dos soluciones. Una, físicamente correcta, en la que la aceleración de la partícula cargada es cero y la partícula permanece en reposo o en movimiento rectilíneo uniforme (y por tanto no irradia campo electromagnético). Pero también otra en la que la partícula se acelera exponencialmente en el tiempo. Esta solución no es física y debe ser descartada manualmente.

Existen soluciones parciales para este problema. Una consiste en escribir la ecuación de movimiento en forma integro-diferencial, pero aunque eso remueve la solución acelerada, rompe la causalidad (¡aunque por tiempos muy cortos!). La solución completa del problema requiere considerar ecuaciones de movimiento relativistas, y el acoplamiento del campo electromagnético con la materia como se hace en la electrodinámica cuántica. Sin embargo eso no significa que no se puedan considerar problemas de acoplamiento de campos electromagnéticos y materia en el régimen clásico. Por ejemplo, en la aproximación cuasiestacionaria que vimos en clase ninguno de estos problemas aparecen. Y en los casos clásicos o semiclásicos que involucran frenado por radiación, se pueden usar aproximaciones o descartar las soluciones espurias.