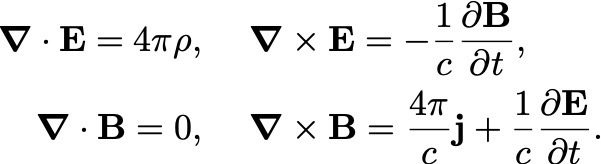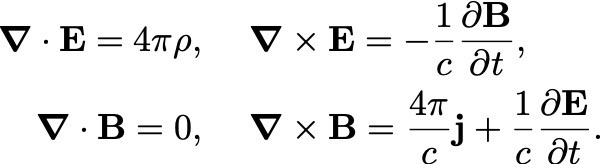El 30 de octubre de 1938, Orson Welles, quizás el mejor director de cine de todos los tiempos (quien dirigió entre otras películas a Citizen Kane, una enciclopedia sobre cómo dirigir una película), hizo en la radio una versión teatralizada de “La guerra de los mundos“, la novela de ciencia ficción de H.G. Wells. En la novela marcianos invaden la Tierra y e inician una guerra contra la humanidad a escala global. Considerando las recientes observaciones de fosfano en Venus la temática de la novela de Wells es muy actual, aunque probablemente en este momento deberíamos estar saludando, en lugar de a los marcianos, a nuestros nuevos señores venusinos:

Orson Welles (cuya voz privilegiada pueden escuchar en el primer video) presentó la novela en la radio como un programa de noticias. En lugar de narrar la novela con la voz de otros actores leyendo algún diálogo, Welles pasó música (que interrumpió para presentar supuestas noticias urgentes sobre explosiones observadas en Marte), entrevistó actores en roles de científicos, y cambió las fechas y lugares de la novela para que la llegada de los marcianos ocurriese ese mismo día y en lugares de la costa este de los Estados Unidos. Y aunque al inicio del programa se presenta claramente a la transmisión como “Orson Welles and The Mercury Theater on the Air in ‘The War of the Worlds’”, varios desprevenidos que escucharon la transmisión ya comenzada pensaron que realmente correspondía a un programa de noticias, y que los marcianos habían invadido la Tierra. Esto catapultó a Orson Welles a la fama, y generó sucesos de histeria colectiva que se han vuelto famosos (aunque la gravedad de los sucesos probablemente haya sido exagerada en los días siguientes por los diarios).

La guerra imaginaria de Orson Welles tuvo un preludio muy real 60 años antes, en una guerra para desarrollar aplicaciones de la teoría electromagnética sin las cuales Welles no hubiera podido emitir su programa de radio (o, al menos, nadie hubiera podido escucharlo). Los principales actores en este enfrentamiento fueron Thomas Edison, Nikola Tesla, y George Westinghouse. Y la guerra se conoce hoy como la guerra de las corrientes (como título, no tiene nada que envidiarle a “La guerra de los mundos”).

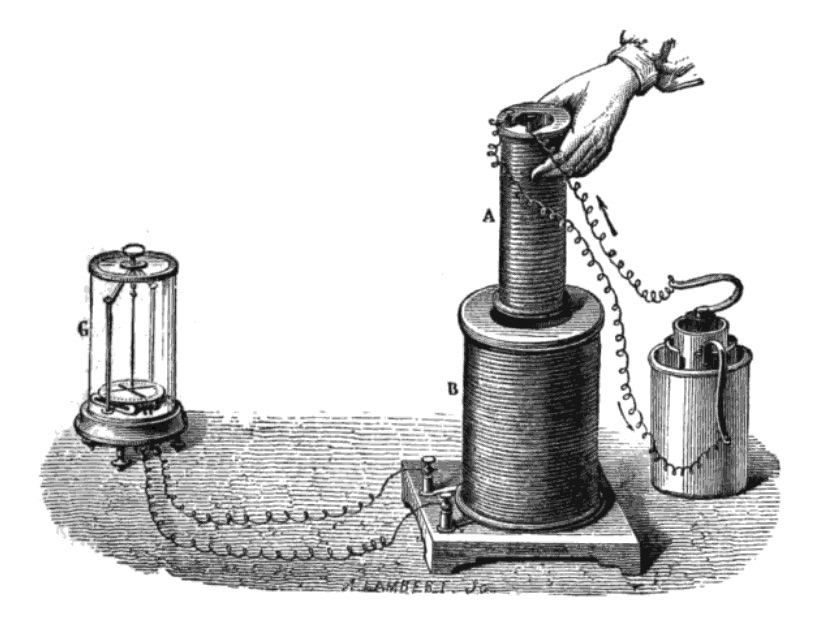
Como vimos en un post anterior, Faraday inventó el primer generador eléctrico usando el fenómeno de inducción que había descubierto en sus experimentos. Hacia fines del siglo XIX Tesla inventó un generador de corriente alterna (AC) más práctico (aunque otros en la misma época inventaron generadores aún más prácticos), y más tarde inventaría un motor de corriente alterna similar a los que usamos hoy. Tesla, que en ese momento trabajaba en la compañía eléctrica de Edison, intentó convencer a Edison de la conveniencia de usar corriente alterna en las casas. Pero por razones monetarias (Edison ya había invertido mucho dinero en un sistema de corriente continua, o DC) Edison rechazó esa idea. Tesla terminó siendo contratado por Westinghouse, un ingeniero dueño de la compañía eléctrica Westinghouse, quién compró además las patentes de Tesla. Con esas patentes, generadores de la empresa Siemens, y un transformador inventado en Europa, Westinghouse trató de vender su sistema de tendido eléctrico para los hogares con corriente alterna. Obviamente el inicio de la batalla entre estos dos sistemas merece ser musicalizado por AC/DC:

Ambas empresas iniciaron largas campañas para vender sus sistemas a las ciudades que comenzaban a instalar tendidos eléctricos para los hogares. Desde el punto de vista de la eficiencia, el sistema AC era muy superior al sistema DC, y lentamente fue ganando preponderancia. En 1888 la compañía de Edison decidió que era el momento de iniciar campañas mediáticas más directas (y menos honestas) contra la corriente continua. Acusaron a la corriente continua de ser más peligrosa, y hasta pagaron una especie de circo itinerante que recorría ciudades electrocutando animales con corriente continua para mostrar sus riesgos (la invención de la silla eléctrica fue un subproducto de esta guerra). A pesar de la campaña de Edison y su empresa, la mayor eficiencia del sistema de corriente alterna terminó ganando la pelea y para 1890 la mayoría de las empresas de distribución eléctrica usaban este sistema (que usamos hoy en todas nuestras casas).

Cerrando el ciclo de comics y el electromagnetismo, los que quieran leer más sobre esta historia pueden mirar un cómic corto (y un poco infantil en la visión de los roles de cada uno de los actores de esta batalla) realizado por la American Physical Society:

• Nikola Tesla and the electric fair.

En 2010, Scott Pilgrim fue adaptado al cine (la película está disponible en Netflix). Si bien fue un fracaso en taquilla, y el personaje de Scott en la película por momentos puede ser irritante, la película captura muy bien la estética del cómic original y más tarde se volvió una película de culto. Superman, Capitán América y Capitana Marvel aparecen en la película (¡no en esos roles!). Y el director, Edgar Wright, dirigió varias películas interesantes, entre las que recomiendo dos películas en las que actúa el dúo humorístico británico formado por Simon Pegg y Nick Frost: Shaun of the dead y Hot Fuzz (como verán, esta materia también da un servicio, y les deja recomendaciones de películas para el fin de semana).

Con la película de Scott Pilgrim podemos adentrarnos en el round 3 (y último por el momento) de las batallas de Maxwell para defender las ecuaciones de sus sueños. Y esta batalla será contra la mecánica cuántica. Las cuatro leyes empíricas detrás de las ecuaciones de Maxwell (asociadas a los experimentos de Coulomb, Ampère y Faraday, y a la inexistencia de monopolos magnéticos) son compatibles con observaciones y experimentos en escalas muy grandes y muy pequeñas. Por ejemplo, la ley de Coulomb es compatible con experimentos para separaciones entre cargas en distancias que van desde 10⁸ m hasta 10⁻¹⁶ m. En resumen, el comportamiento del mundo microscópico es, hasta donde hoy sabemos, compatible con las leyes detrás de las ecuaciones de Maxwell.

Sin embargo, el campo electromagnético clásico en las ecuaciones de Maxwell no está cuantizado. Pero eso no es un problema, porque las ecuaciones de Maxwell son las ecuaciones de onda para un fotón. Cuantizarlas cambia la interpretación física de los campos E y B, pero no agrega ni quita términos en las ecuaciones. La radiación de cuerpo negro, que corresponde a la emisión de fotones en equilibrio térmico por una fuente, satisface las ecuaciones de Maxwell tal como las vemos en esta materia.

La convivencia de Maxwell con la nueva física del siglo XX no fue lecho de rosas (para la nueva física). La ecuación de Schrödinger, como las ecuaciones de Newton, no es relativista. Es decir, la ecuación de Schrödinger es invariante de Galileo. Acoplar ciertos fenómenos cuánticos con el electromagnetismo no requirió modificar al electromagnetismo, sino modificar la mecánica cuántica para considerar el caso relativista. Nuevamente las ecuaciones de Maxwell resultaron victoriosas. Pero en la descripción cuántica-relativista las cosas se ponen difíciles. El número de partículas puede cambiar en el tiempo vía los procesos de creación y destrucción de pares: un fotón puede generar pares de partículas, siempre conservando la carga (como al crear un electrón y un positrón). La descripción de estos fenómenos es hoy descripta por la electrodinámica cuántica, que es la teoría que acopla correctamente al electromagnetismo y la materia en el caso cuántico-relativista. Esta teoría, por la que Sin-Itiro Tomonaga, Julian Schwinger y Richard Feynman ganaron el premio Nobel en 1965, es increíblemente precisa y compatible con los experimentos hasta el momento. Y algunas propiedades que conocemos del electromagnetismo clásico, como el principio de superposición, se pierden: el hecho de que el número de partículas pueda cambiar permite que un fotón interactúe con otro fotón. Pero esto no es el resultado de una corrección a las ecuaciones de Maxwell, sino del acoplamiento de las ecuaciones de Maxwell con la cuántica (y con la materia). Los que quieran aprender más sobre esto, qué mejor que hacerlo escuchando a uno de los creadores de la teoría:

En resumen, las ecuaciones de Maxwell no cambiaron a lo largo del siglo XX, aún durante la revolución de la mecánica cuántica. Las ecuaciones que hoy conocemos para los fenómenos electromagnéticos son las mismas que Maxwell escribió en 1861. Y no son una aproximación clásica que requiera correcciones en el caso cuántico. Para un solo fotón en vacío, las ecuaciones de Maxwell siguen siendo las ecuaciones de la física compatibles con las observaciones experimentales.

Aviso: Considerando el anuncio de último momento sobre el día del estudiante el 21 de septiembre, y el apretado cronograma de la materia, luego de las conversaciones que tuvimos en la última clase hemos decidido dictar clases por Zoom el lunes. Quienes no quieran o puedan conectarse pueden ver la clase grabada el día siguiente, y pueden enviar sus consultas al foro.

Scott Pilgrim es un cómic canadiense creado por Bryan Lee O’Malley (también hay una película, pero eso será tema de un próximo post). El comic sigue las aventuras de Scott, que luego de enamorarse perdidamente de Ramona Flowers, descubre que la relación con Ramona tiene duras condiciones: debe enfrentarse con sus siete ex diabólicos (por diversos motivos, este tipo de cosas siempre se descubren demasiado tarde). Por enfrentarse, me refiero a que debe ganar una pelea. Y cada uno de los ex de Ramona es alguien famoso, fuerte, o con superpoderes. El cómic, que explora entre otras cosas las consecuencias de las relaciones tóxicas, combina el estilo del cómic norteamericano con el del manga y los videojuegos (por ejemplo, la banda de rock de Scott Pilgrim se llama “Sex Bob-omb”, una referencia a los Bob-omb de Super Mario). Casualmente hace dos días (el 13 de septiembre) se cumplieron los 35 años del lanzamiento de Super Mario Bros.:

Como Scott Pilgrim, James Maxwell también descubrió que para escribir las ecuaciones de sus sueños debía enfrentarse a varios ex malvados de la física. Sus ecuaciones eran, y fueron, incompatibles con varias otras teorías. Maxwell no llegó a ver el final de varios de esos enfrentamientos, pero su teoría los ganó a todos. En más de un sentido sus ecuaciones son las primeras ecuaciones de la física contemporánea, que iniciaron (antes que la cuántica) una revolución que afectaría fuertemente a toda la física en la primera mitad del siglo XX. Y sus ecuaciones no cambiaron ni en un solo término, a pesar de todos los cambios que tuvo la física en ese período. Como Samwise Gamgee en El señor de los anillos, Maxwell tal vez sea el héroe anónimo de la física moderna, opacado por otros grandes nombres que se subieron a sus hombros para poder ver mas lejos.

El primer round de Maxwell contra los ex malvados (¡round 1!) fue nada más y nada menos que contra el mismísimo Isaac Newton. En 1861, las ecuaciones de Newton y su Principia Mathematica tenían 174 años sin que nadie se atreviese a discutir su validez. Pero la fuerza electromagnética tiene un problema. Para una carga puntual q que se mueve con velocidad v, la fuerza electromagnética en unidades cgs-Gaussianas está dada por la fuerza de Lorentz (donde c es la velocidad de la luz):

Las leyes de Newton nos dicen que dos observadores en sistemas inerciales que se mueven con velocidad constante uno respecto al otro deben medir la misma fuerza. Pero también según Newton, si un observador S’ se mueve con velocidad constante u respecto a nuestro sistema de referencia S, el observador S’ verá que la carga se mueve con una velocidad relativa v‘ = v - u. La igualdad de la fuerza para ambos observadores implica que si nosotros vemos campos eléctricos y magnéticos E y B, el observador S’ debe ver campos B‘ = B y E‘ = E – u x B/c. Sin embargo, las ecuaciones de Maxwell no son compatibles con esta transformación para los campos frente a un cambio en el sistema de referencia (¡prueben hacer la cuenta y verán que las ecuaciones cambian!). Así, o las ecuaciones de Newton están mal, o las ecuaciones de Maxwell están mal. Alguien iba a salir lastimado de este enfrentamiento.

Como sabemos, este round lo ganó Maxwell (¡Game over!). La teoría de la relatividad especial de Einstein modificó la mecánica clásica, e introdujo nuevas transformaciones frente a un cambio de sistema de referencia que preservan la invariancia de las ecuaciones de Maxwell. En 1905, las ecuaciones de Maxwell seguían siendo las mismas que las que Maxwell escribió en 1861. Las ecuaciones que fueron modificadas fueron las de la mecánica de Newton, no las del electromagnetismo. Más adelante en la materia veremos este problema, y su resolución, en detalle.

¡Round 2!: Hace unos días Juan Pablo Pinasco (@jpinasco) del Departamento de Matemática me mandó un paper muy interesante, con una demostración de las ecuaciones de Maxwell que contó alguna vez Feynman (¿a modo de broma?), y que Freeman Dyson formalizó y puso por escrito:

• Feynman’s proof of the Maxwell equations.

Feynman parte de las ecuaciones de Newton y las relaciones de conmutación en cuántica, y obtiene dos de las ecuaciones de Maxwell (Dyson considera que las otras dos ecuaciones de Maxwell meramente definen las fuentes). Pero son las otras dos ecuaciones (y la conservación de la carga en particular) las que hacen imposible sostener la invariancia de Galileo en el electromagnetismo. Como Dyson mismo comenta (y otros autores en sus cartas al editor en el mismo archivo), el argumento de Feynman debe ser interpretado mas bien como una verificación de la consistencia de la física que conocemos. ¡Maxwell también gana este round!

Aprovecho para avisar que el Campus Virtual de Exactas tiene algunos problemas; esperamos que se resuelvan pronto para que puedan hacer todas sus consultas en los foros. Y para cerrar este primer posteo de los enfrentamientos de Maxwell con la física con una temática más ligera que la de los posteos previos del ciclo de cine de terror e historia del electromagnetismo (que puede haber impresionado a algunos), les dejo un video con una versión animada del cómic de Scott Pilgrim:

En esta última entrega de la serie de películas de terror (¡por el momento!), tenemos una de las mejores de películas de John Carpenter. “La cosa” (The thing, 1982) cuenta la historia de un grupo de investigadores encerrados en una base norteamericana en la Antártida, que debe enfrentarse a un parásito extraterrestre. El parásito no se puede destruir, y se transforma en el organismo que invade (y más tarde puede transformarse en otras cosas). Es un clásico del cine de terror y de la ciencia ficción, y una película de culto que pueden ver en Netflix. No solo la película es fuertemente recomendada para aprobar esta materia, sino que la temática general (con personas aisladas y encerradas, y tests de sangre para detectar un virus) es ideal para los tiempos que vivimos.

El concepto de que “nada se pierde, todo se transforma” se basa en la observación de la naturaleza. Tal vez el primero en ponerlo en estos términos fue Antoine Lavoisier, en el marco de sus experimentos en química. Pero en física hoy conocemos formalmente esta idea en la forma de leyes de conservación: ciertas cantidades en la naturaleza no cambian aún si un sistema aislado evoluciona en el tiempo. James Clerk Maxwell fue el primero en notar que las expresiones empíricas que se seguían de las observaciones experimentales de Coulomb, Ampère y Faraday no conservaban la carga eléctrica: la carga eléctrica según las ecuaciones del electromagnetismo de la época podía ser creada o destruida de la nada. Pero la evidencia experimental hasta ese momento indicaba que la producción de una carga positiva venía siempre acompañada por una carga negativa, es decir, que la carga total en un sistema aislado no puede cambiar (algo que se sigue verificando experimentalmente hasta el día de hoy). Maxwell entonces modificó las expresiones agregando el famoso término de la corriente de desplazamiento, de forma tal que las ecuaciones del electromagnetismo conserven la carga eléctrica total:

Como vimos en clase, de izquierda a derecha y de arriba hacia abajo, estás ecuaciones se obtienen respectivamente de la fuerza de Coulomb, de los experimentos de Faraday (que Maxwell escribió en esta forma), de la no observación de cargas magnéticas, y de las observaciones de Ampère. El último término en esta ecuación fue agregado por Maxwell para conservar la carga. Y aquí aparece la genial Emmy Noether:

Uno de los teoremas más importantes en la física teórica moderna, el teorema de Noether, nos dice que cada ley de conservación está asociada a una simetría. ¿A qué simetría se asocia la conservación de la carga? La conservación de la carga está asociada a la simetría de gauge del electromagnetismo. Sabemos que, por ejemplo, podemos sumarle una constante C a cualquier potencial φ, y obtener el mismo campo eléctrico

Es decir, podemos elegir arbitrariamente el cero del potencial. Y también sabemos que el trabajo necesario para desplazar una carga q entre dos puntos 1 y 2 con diferentes valores del potencial es W = q(φ₂ – φ₁). Luego, si fuera posible crear cargas de la nada, el trabajo necesario para crear una carga en un punto cualquiera debería ser qφ. Pero esto nos permitiría determinar el valor absoluto del potencial electrostático φ (¡y determinar en forma absoluta el cero del potencial!) simplemente midiendo el trabajo necesario para crear la carga q. Así, la conservación de la carga y la libertad de gauge del electromagnetismo están relacionadas: si la carga total no se conserva, podemos determinar en forma única el cero de los potenciales.

La conservación de la carga implica que no podemos cambiar la cantidad total de carga en el universo. Pero esto no implica que el universo tenga una carga eléctrica total igual a cero. Podría haberse originado con un desbalance de carga (por ejemplo, más cargas positivas que negativas), y por la conservación de la carga, el desbalance total de carga hoy debería ser el mismo que al inicio del universo. Pero toda la evidencia observacional hasta el momento indica que el universo es eléctricamente neutro. Por ejemplo, un desbalance de carga generaría campos eléctricos que impondrían una dirección privilegiada en el espacio y una anisotropía en la radiación cósmica de fondo, o una anisotropía en los rayos cósmicos que llegan a la Tierra. Nada de eso se observa. Si hay un desbalance de carga en el universo, debe ser muy pequeño.

No dejen de ver este y este anuncio importante sobre la práctica, y en la página de la teórica ya pueden encontrar los apuntes para la próxima clase y el video de la clase del miércoles.

La película es “La novia de Frankestein” (1935), y el monstruo es protagonizado por el mítico Boris Karloff y Elsa Lanchester. En la novela original de Mary Shelley el monstruo también pide que le construyan una pareja, o en caso contrario amenaza con matar a toda la familia del profesor Frankestein (un caso interesante y bastante literal de “publish or perish“). Pero el profesor Frankestein se niega a dar vida a otro monstruo. Sin embargo, en esta secuela a una película original sobre Frankestein y su monstruo de 1931, el profesor hace lugar al pedido. La vida se insufla, tanto el monstruo como en su novia, con electricidad. La imagen de la novia de Frankestein (Elsa Lanchester), con su pelo en forma cónica y la onda blanca en forma de rayo a los costados, se ha vuelto una imagen icónica en la cultura popular. Todas las películas recientes sobre la historia de Frankestein no están a la altura de estas primeras películas: esta imagen, como la imagen clásica de Karloff en el papel del monstruo, con la frente amplia y los electrodos a los costados del cuello, se han vuelto imágenes de culto.

Mary Shelley escribió Frankestein en 1818. A fines del siglo XVIII Galvani y Volta hicieron una serie de experimentos en los que mostraron que hacer circular electricidad por la pata de una rana muerta contraía sus músculos, y la pata se movía. Los experimentos tuvieron un impacto importante en la cultura popular de la época e inspiraron a Mary Shelley. El descubrimiento tuvo también aplicaciones médicas en la electroterapia moderna, en el marcapasos, y el desfibrilador.

Los experimentos de Galvani y Volta forman parte de la serie de experimentos que entre los siglos XVIII y XIX establecieron las leyes fundamentales del electromagnetismo tal como hoy las conocemos. Y la serie de experimentos más influyentes fue realizada por Couloumb, Ampère, y Faraday. Couloumb usó materiales cargados eléctricamente y una balanza de torsión para determinar que la fuerza electrostática de atracción o repulsión entre las cargas es proporcional al producto de las cargas e inversamente proporcional a la distancia que las separa. Coulomb publicó tres trabajos con estos resultados experimentales a partir de 1785. La imagen de su balanza de torsión se muestra a continuación. Le permitió medir con mucha precisión la fuerza de atracción o de repulsión entre cargas, y poniendo las cargas a diferentes distancias (una sobre el brazo de la balanza de torsión, y desplazando libremente a la otra), mostrar que la fuerza decrecía con el cuadrado de la distancia que separaba a ambas cargas (básicamente, midiendo el ángulo en que se movía el brazo de la balanza):

Ampère hizo experimentos con cables, corrientes, y brújulas, continuando experimentos que fueron realizados primero por Ørsted en 1820. Ampère rápidamente se dio cuenta que la aguja de una brújula se alinea a lo largo de círculos concéntricos cuando la brújula me mueve en el plano perpendicular a un cable recto por el que circula una corriente. Y realizó experimentos para medir la fuerza entre dos cables rectos por los que circulan diferentes corrientes. Pero determinar una expresión para la fuerza magnetostática es mucho más difícil que en el caso electrostático considerado por Couloumb. La fuerza cambia de acuerdo a cómo se alinean los cables y a la dirección en la que circulan las corrientes, y construir evidencia experimental confiable requiere muchos más experimentos, con muchas más configuraciones (y muchos más papers), que los tres papers publicados por Coulomb a fines del siglo XVIII. Para comprender esto basta comparar la expresión moderna de la fuerza de Coulomb con la de la fuerza magnetostática en la ley de Biot-Savart (1820), ambas en el sistema de unidades cgs-Gaussiano:

Mientras que la primera fuerza solo involucra dos magnitudes escalares (las cargas q₁ y q₂, respectivamente en posiciones r₁ y r₂), la segunda expresión involucra magnitudes vectoriales asociadas a las direcciones de las corrientes I₁ e I₂ a lo largo de dos cables, y las integrales sobre todo el recorrido de ambos cables.

Algo parecido ocurrió con los experimentos de Faraday. Y el caso de Faraday brinda además un ejemplo interesante de cómo se comunicaba la ciencia en el siglo XIX, y cómo se sigue comunicando hoy. Entre 1821 y 1832 Faraday hizo una gran cantidad de experimentos estudiando el fenómeno de inducción, creando el primer generador (un dínamo), e identificando con éxito la relación entre corriente y voltaje. En su serie de experimentos más importante, condensada en la ley de Faraday en las ecuaciones de Maxwell, usó dos cables aislados para mostrar que al variar en el tiempo la corriente que pasa por uno de los cables, otra corriente es inducida en el segundo cable. Uno de sus experimentos se veía aproximadamente así:

Las dos bobinas (A y B) están enrolladas alrededor de un mismo núcleo, pero aisladas entre si. La corriente en la bobina A se hace variar en el tiempo conectando y desconectando la batería que se encuentra a la derecha. Y el galvanómetro G, a la izquierda, se usa para detectar la corriente inducida en la bobina B al conectar y desconectar la bobina A. Este tipo de experimentos suele contarse como si fueran experimentos demostrativos. Pero para determinar expresiones empíricas para las fuerzas eléctrica, magnética, y electromotriz, fue necesario construir y publicar grandes cantidades de tablas. Solo en la revista Philosophical Transactions of the Royal Society, Faraday publicó más de 30 papers y reportes con diferentes configuraciones y mediciones de sus experimentos, la mayoría de ellos en una serie de trabajos numerados con el título “Experimental researches in electricity” (¡y los papers fueron refereados por pares!). Es decir, ya en 1832 Faraday comprendía la importancia de publicar sus resultados (aunque fueran preliminares) luego de ser evaluados por colegas, y de comunicar lo aprendido brindando explicaciones de los detalles, las limitaciones de sus experimentos, valores para cada una de sus mediciones, y estimaciones de los errores experimentales. Más allá de las discusiones contemporáneas sobre “publish or perish” y las prácticas actuales de ciertas editoriales científicas, el deseo por comunicar lo que uno descubre es atemporal, y la mayoría de los grandes físicos en la historia generaron gran cantidad de trabajos para sostener el diálogo con sus colegas, discutir, y aprender de los resultados de otros.

Los que quieran leer más sobre la historia temprana del electromagnéticos, y especialmente sobre los papers publicados por Faraday describiendo sus experimentos, pueden leer este paper reciente en Philosophical Transactions of the Royal Society:

• The birth of the electric machines

En la novela “El resplandor (The shining)” de Stephen King, Danny Torrance es un chico con habilidades psíquicas: puede leer mentes, tener premoniciones, y hablar con fantasmas (como comentario al margen, yo viví por más de cuatro años en la misma calle en la que, en la novela, vive la familia Torrance, y a pocas cuadras del lugar en donde vive la familia en la película). La novela fue adaptada para el cine por Stanley Kubrick en 1980. La película, en la que Kubrick tomó varias libertades respecto a la historia original en la novela, es un clásico del terror psicológico que les recomiendo para el fin de semana. Y también fue genialmente homenajeada en un especial de Halloween de Los Simpsons (“Sin televisión y sin cerveza Homero pierde la cabeza”).

Como en El resplandor y en buena parte del cine de terror, los sucesos contrarios a lo que parece natural suelen generar horror o fascinación en las personas (o ambas cosas). No por nada Einstein catalogó a un extraño efecto cuántico como “spooky action at a distance” (o escalofriante acción a distancia). Y a lo largo de los siglos, la acción a distancia asociada a las fuerzas electromagnéticas, y la capacidad de mover cosas sin tocarlas, ha generado ambas reacciones en las personas. La gravedad es otro ejemplo de acción a distancia, pero las escalas involucradas son tan grandes que nos resulta más natural (o menos manipulable). Con las fuerzas electromagnéticas podemos controlar cosas en escalas humanas. Podemos usar un imán para atraer a la distancia a un material paramagnético, o usar al mismo imán para sostener un papel pegado a la heladera, algo que a todas luces es muy extraño (y para nada fácil de explicar). Claro que todos estos efectos no son inmediatos, se propagan a la velocidad de la luz. Actúan a la distancia, pero con una velocidad de propagación finita.

Aunque hoy nos parezca natural comunicarnos con ondas de radio (¡pero no a todo el mundo le resulta natural, y muchas personas divulgan teorías conspirativas sobre la llegada del 5G!), poder ejercer fuerzas a distancia generó miedo y pánico en muchas generaciones. No es casual que el profesor Frankestein haya dado vida a su monstruo usando electricidad, un tema al que regresaremos en un próximo post. Ni es casual la fascinación de Tesla y de los primeros escritores de ciencia ficción con el rayo de la muerte. Los reportes pseudocientíficos de actividad paranormal, avistamientos de OVNIs y poderes psíquicos suelen venir acompañados por variopintas descripciones de campos electromagnéticos, autos que se apagan espontáneamente, y ruido blanco en las señales de radio y televisión. Poder controlar a gusto campos electromagnéticos es, en el imaginario popular, algo sobrenatural (cuando la realidad es que esto es algo que hacemos diariamente). Y desde el miedo primitivo de nuestros antepasados a los rayos en las tormentas eléctricas, hasta el reciente uso por David Lynch del tendido eléctrico como un portal a otras dimensiones en Twin Peaks, el electromagnetismo ha sido para muchos un fenómeno misterioso que no debemos subestimar.

La teoría física del electromagnetismo tal como hoy la conocemos comenzó a gestarse a partir de experimentos que se realizaron a fines del siglo XVIII y en el siglo XIX. Hacia fines de ese siglo Maxwell condensó todos los resultados en las famosas ecuaciones que llevan su nombre, que en vacío y en el sistema de unidades cgs-Gaussiano toman la forma

Estas ecuaciones rápidamente permitieron descubrir nuevos fenómenos físicos, que encontraron aplicaciones que seguimos usando hoy. Ya no nos sorprende poder comunicarnos usando ondas de radio (¡o no debería!). Ni el uso de radares, o de antenas de celulares y señales de WiFi. Pero en esta materia deben volver a sorprendernos. Debemos ver el resplandor de estos fenómenos como Danny Torrance ve a los fantasmas. O, en palabras de Ray Bradbury en Crónicas Marcianas (1950),

“Es bueno renovar nuestra capacidad de asombro -dijo el filósofo-. Los viajes interplanetarios nos han devuelto a la infancia“.

Para entender los fenómenos físicos, debemos volver a preguntarnos qué ocurre en el contorno de un conductor perfecto, por qué el campo eléctrico es más intenso en el entorno de regiones con forma de punta en materiales conductores, y cómo son los campos dentro de un dieléctrico. Son preguntas sencillas, y de física clásica. Pero si podemos comprender esos fenómenos, la teoría electromagnética nos dará herramientas muy poderosas para entender fenómenos mucho mas complicados y que juegan un rol central en la física contemporánea, como la dinámica de los campos magnéticos en estrellas y galaxias, la razón por la cual las estrellas no están donde creemos que las vemos en el cielo nocturno, la física de metamateriales, por qué usamos capacitores cilíndricos, cómo se produce un rayo, o por qué el cielo en nuestro planeta es celeste. Todos estos fenómenos los estudiaremos en la materia, a lo largo de las clases o en posts en esta página web.

En el Campus Virtual y en la página de la práctica encontrarán discusiones interesantes sobre notación de índices. Y como siempre, en la página de la teórica encontrarán el video de la última clase y el material para la próxima clase. Y también todos los notebooks de Python que uso durante la clase. Pierdan el miedo y úsenlos. No es necesario saber programar, no es necesario que lean largos tutoriales de Python, ni que se vuelvan expertos. Solo que se atrevan a escribir “diff(cos(x),x)” en alguno de los notebooks que les pasé con SymPy, y aprieten SHIFT+ENTER. ¡Atrévanse a volar! Todo es muy sencillo:

El electromagnetismo clásico es una teoría muy formal y elegante, pero que también puede resultar tediosa en algunos de sus aspectos matemáticos. A lo largo de la materia haremos muchas cuentas, y es fácil perder el foco pensando que la principal motivación del curso es la formalización, olvidando el origen experimental de la teoría electromagnética. O preguntarnos para qué necesitamos hacer tantas cuentas, o conocer tantas formas diferentes de resolver un mismo problema. Así que este primer post de las clases teóricas va a intentar motivar posibles respuestas a estas inquietudes.

El primer video lo pongo en la página de todos los cursos que dicto (los que ya lo vieron pueden volver a verlo, porque siempre se puede volver a ver a Feynman). El video muestra una clase brillante de Richard Feynman explicando su visión sobre cómo se construye una teoría. Alcanza con mirar el primer minuto:

En el video Feynman dice que la búsqueda de una nueva ley física comienza “adivinándola” (“first, we guess it“). Luego se derivan consecuencias y predicciones a partir de esa ley “adivinada”, y se verifican (o no) esas predicciones con experimentos. Y a continuación Feynman es categórico: “If it disagrees with experiments, it is wrong. And that simple statement is the key to science. It doesn’t make a difference how beautiful your guess is, it doesn’t make a difference how smart you are, or who made the guess or what his name is, if it disagrees with experiments… it is wrong”. En física no hay argumentos de autoridad o de elegancia o belleza que valgan. Esto puede resultar sorprendente en vista a ríos de tinta que se han escrito diciendo lo contrario, pero es el núcleo central de la física concebida como una ciencia natural. Si la teoría está en desacuerdo con los experimentos, está mal. El resto del video continúa con Feynman hablando de platos voladores, pseudociencias, y otros conceptos del método científico. Si tienen tiempo, les aconsejo mirarlo completo. Y los que tengan ganas, pueden mirar el ciclo de charlas (con subtítulos) sobre “El carácter de la ley física” que Feynman dió en Caltech en 1964, del que el video que menciono arriba es solo un breve extracto:

• Richard Feynman’s Messenger Lecture Series.

La teoría electromagnética es un hermoso ejemplo de las ideas de Feynman sobre cómo funcionan las ciencias naturales. Por encima de la elegancia de las ecuaciones de Maxwell, la teoría se construyó a lo largo de muchos años a partir de los experimentos de Coulomb, Faraday, Ampére y muchos otros. Cada una de las ecuaciones de Maxwell sintetiza en forma elegante los resultados de esos experimentos. Y como veremos a lo largo del curso, la evidencia experimental compatible con esta teoría se enfrentó y desplazó a teorías físicas con mucha autoridad, elegantes, y asociadas a grandes nombres, como la mecánica Newtoniana.

¿Y entonces, para qué aprender a hacer tantas cuentas? ¿Para qué vamos a tener que poder reproducir estas cuentas en el examen final? ¿Para qué repetir paso por paso cuentas que ya hicieron otros? Y aquí Feynman también viene al rescate:

Esta es la foto del pizarrón en la oficina de Richard Feynman el día de su muerte. La frase mas citada de este pizarrón es “What I cannot create I do not understand”, pero la que nos va a interesar como motivación para este curso es la que aparece abajo: “Know how to solve every problem that has been solved”, o Saber cómo resolver cada problema que ha sido resuelto. A la derecha pueden ver una lista de problemas que Feynman quería aprender (“To learn”). Esa lista incluye al ansatz de Bethe (un método para encontrar soluciones exactas de un modelo simplificado para materiales antiferromagnéticos), el efecto Kondo (el cambio en la resistividad eléctrica de un metal por el scattering de los electrones en impurezas magnéticas), el efecto Hall en dos dimensiones, la temperatura que mide un observador acelerado en un problema relativista, e hidrodinámica clásica no-lineal. Uno de estos problemas (“Kondo”) aparece tachado, probablemente porque Feynman consideró que ya había comprendido suficientemente bien el tema.

A veces los físicos aparentan que las grandes ideas nacen exclusivamente de su propia genialidad (y Feynman no era ajeno a esta práctica). Pero este pizarrón nos da una visión más humilde y realista de cómo se hace física teórica, y ciencia en general. Feynman, aún a sus 70 años y luego de ganar un premio Nobel, se sentaba con los papers recientes en temas muy diversos, algunos muy lejanos a su área de trabajo, y aprendía a hacer las cuentas paso por paso (“Know how to solve every problem that has been solved”). ¿Por qué? Porque usualmente, cuando vemos un problema nuevo, reconocemos semejanzas con otros problemas que estudiamos y lo intentamos resolver usando las herramientas que aprendimos a usar en otras partes de la física. Muchos de los métodos que aprenderemos en esta materia (como el método de separación de variables, las funciones de Green, o las expansiones multipolares) forman parte de las herramientas que se usan todo el tiempo en física teórica, y aprender a manejarlos cómodamente es lo mínimo que podemos hacer luego de ver los esfuerzos que hacía Feynman a sus 70 años. Y para conseguirlo no hay grandes secretos, hay que sentarse y hacer los problemas de las guías de trabajos prácticos, hacer preguntas, consultar las dudas, y pasar horas ejercitando.

Cómo a lo largo de la materia habrá muchos posteos como este, y la práctica también tendrá noticias y avisos que hacer, para facilitar la navegación vamos a marcar los posteos con categorías (“Teóricas”, “Prácticas” y “Novedades” por el momento, aunque podremos agregar más en el futuro). En el menú a la derecha en la página de la materia van a encontrar la lista de las categorías, y apretando en una de ellas podrán ver solo los posteos que correspondan a esa categoría. ¡Ah, y en la página de la teórica ya está disponible el video de la primer clase teórica de la materia, el link al video en YouTube, y material para la próxima clase! Y en este post, y en la página de la práctica, encontrarán los apuntes de la clase práctica de ayer. Recuerden que pueden canalizar cualquier duda, pregunta o crítica en los foros del Campus Virtual. Allí encontrarán varios foros ya creados para consultas sobre las clases teóricas, sobre la guía 1 de ejercicios, y para hacer sugerencias. No duden en añadir nuevos temas de conversación en cada uno de estos foros siguiendo las reglas que figuran al inicio de cada uno.