En esta escena de la película El lobo de Wall Street, dirigida por Martin Scorsese (uno de los grandes directores de la historia del cine), Matthew McConaughey habla la “fugacidad” de la bolsa de valores. Llamativamente, la lírica de la canción “Money“, de Pink Floyd (del disco The Dark Side of the Moon, y que forma parte de la playlist de la materia), tiene la memorable frase “Money, it’s a gas“. Y aparentemente ninguna de estas frases es simplemente una licencia poética. En muchos sentidos hay conexiones profundas entre la mecánica estadística y el modelado de los mercados bursátiles, que en algunos casos se remontan hasta los inicios de la teoría.

Los que tengan curiosidad sobre cómo se usan herramientas de mecánica estadística para el estudio de economía y finanzas pueden mirar este muy buen review:

• Colloquium: Statistical mechanics of money, wealth and income

que fue publicado en Reviews of Modern Physics en 2009. El artículo es introductorio y explica varios de los conceptos que se usan comúnmente en el área de econofísica, incluyendo modelos estocásticos (como los modelos de camino al azar que vimos en clase), cómo se usa el ensamble canónico (o de Gibbs) y el ensamble gran canónico, los vínculos asociados a la “conservación del dinero”, o los vínculos que se usan en sistemas más realistas en los que pueden existir deudas y cómo esto resulta en diferentes equilibrios estadísticos. En particular, la Sección I, y la Sección II desde la subsección A hasta la C, se leen fácilmente, y usan muchos de los conceptos que introdujimos hasta ahora en la materia.

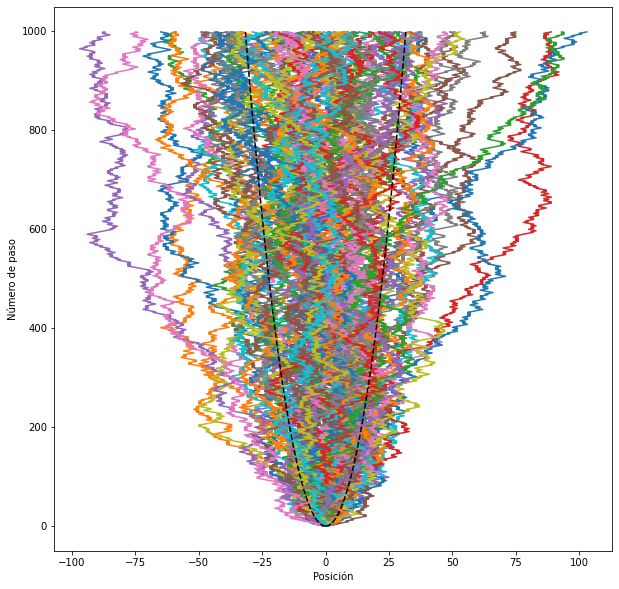
En las secciones II.B y II.C, los autores reemplazan el vínculo sobre la energía que usamos al derivar los ensambles, por un vínculo sobre el dinero total circulante. Si asumimos que el dinero total se conserva, la distribución de probabilidad de equilibrio para el dinero está dada por la distribución de Boltzmann-Gibbs,

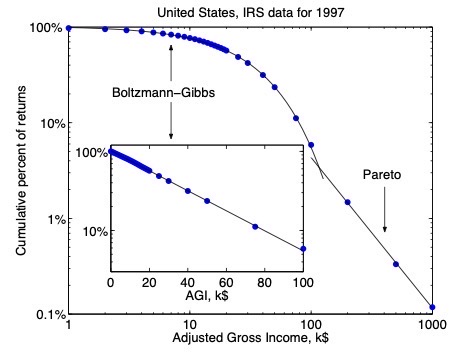
donde m es la cantidad de dinero, y T_m es la “temperatura estadística” del sistema (es decir, el multiplicador de Lagrange). Esta cantidad (T_m) es igual al dinero medio disponible por persona. Noten que esta expresión para la probabilidad es formalmente igual a la obtenida en el ensamble canónico. Excepto por casos con ingresos extremadamente grandes (que deben ser modelados con otra distrubución de probabilidad, la distribución de Pareto), la distribución de Boltzmann-Gibbs está en buen acuerdo con los datos de muchos países. A modo de ejemplo, el review compara este resultado con la probabilidad acumulada en función de los ingresos de los individuos usando datos de la oficina de impuestos de los Estados Unidos.

En esta figura los puntos azules son datos (porcentaje acumulado de casos en función de los ingresos brutos ajustados de cada contribuyente), y la linea negra de la izquierda corresponde a la distribución de Boltzmann-Gibbs (o la distribución canónica), seguida por la distribución de probabilidad de Pareto.

Este artículo tiene también un hallazgo interesante sobre la visión amplia que tenía Boltzmann de la física, que más de 100 años atrás vislumbró la aplicabilidad de la mecánica estadística tanto en física como en otras áreas muy diversas del conocimiento (una visión que se cumplió con creces). En 1905 Boltzmann, hablando sobre la generalización y formalización de la mecánica estadística realizada por Gibbs, escribió:

“Esto abre una perspectiva amplia, si no pensamos solamente en objetos mecánicos. Consideremos aplicar este método a la estadística de seres vivos, de la sociedad, en sociología, etc.”

Boltzmann tomó algunas ideas de estadística que ya se aplicaban en su época en el estudio de la sociedad para construir su teoría de los gases diluidos. Así que su propuesta de aplicar la incipiente mecánica estadística en estudios de la sociedad y en sociología podría resultar esperable. Hoy esta aplicación en particular recibe el nombre de sociofísica; el grupo de Pablo Balenzuela (@polbalen) trabaja en estos temas en el Departamento de Física. Y la famosa novela de ciencia ficción “Fundación“, de Isaac Asimov, también juega con la idea de aplicar la teoría de gases diluidos en las ciencias sociales para predecir el posible desarrollo de una sociedad.

Las aplicaciones actuales de la mecánica estadística en biología, economía, y otras ciencias pueden resultar aún más inesperadas. Los que quieran mirar un ejemplo más reciente de aplicaciones en economía pueden leer este artículo en Nature Communications sobre eventos extremos en sistemas macroeconómicos.

El posteo de hoy gira alrededor del espíritu general de esta materia, y de nuestro enfoque de la mecánica estadística, inspirado en parte en este video de Richard Feynman:

Como mencioné en el aula, en esta materia no vamos a demostrar ni a derivar la termodinámica. Esta materia es, en cierto sentido, una materia sobre jerarquías en la naturaleza. No siempre podemos derivar un comportamiento complejo como resultado directo de leyes fundamentales. Muchas, muchísimas veces, al trabajar con sistemas complejos o extensos necesitamos hacer aproximaciones, e introducir conceptos que (aunque tienen vínculos con las leyes fundamentales de la naturaleza) tienen sentido solo en forma aproximada (¡como el calor!). Justamente en este video Feynman dice (en el minuto 0:22): “For example, at one end we have the fundamental laws of physics. Then we invent other terms for concepts which are approximate, which have, we believe, their ultimate explanation in terms of the fundamental laws. For instance, ‘heat’. Heat is supposed to be the jiggling, and the word for a hot thing is just the word for a mass of atoms which are jiggling.” (“Por ejemplo, en un extremo tenemos las leyes fundamentales de la física. Luego inventamos otros términos para conceptos que son aproximados, que, creemos, tienen su explicación última en términos de las leyes fundamentales. Por ejemplo, el “calor”. Se supone que el calor es la vibración, y la palabra para algo caliente es solo la palabra que usamos para una masa de átomos que se sacuden.”).

Noten que Feynman no intenta convencernos de que hay una expresión formal y correcta para el calor en términos de leyes o magnitudes físicas fundamentales. Nos dice que el calor es un concepto aproximado para describir ciertos fenómenos en una escala macroscópica. Muchos conceptos en termodinámica son de este tipo: algunos podremos formalizarlos, para otros necesitaremos muchas aproximaciones. Y la descripción microscópica que construiremos será compatible (por diseño y construcción) con la termodinámica, porque si la violase construiríamos otra teoría microscópica. El enfoque de esta materia nos puede ayudar a entender ciertos sistemas físicos de otra forma, pero no se confundan y piensen que porque una teoría se deriva con más cuentas y trabajo es necesariamente mejor. Porque es imposible unir las dos descripciones (la macroscópica y la microscópica) sin hacer muchas aproximaciones en el medio, de forma tal que más que ser la segunda descripción más perfecta o formal, no podría existir si no comprendiésemos muy bien la primera. En cierta forma, esta materia cumple al pie de la letra una frase que probablemente nunca fue dicha por Groucho Marx: “Éstos son mis principios, y si no le gustan, tengo otros“.

Sobre este punto, en el video Feynman dice algo muy interesante, y que va contra la concepción simplista de la física que imagina que entender un fenómeno se reduce siempre a reducirlo a las leyes o principios fundamentales que están detrás. En el video Feynman continúa hablando de sistemas cada vez mas complejos, y aproximaciones cada vez mayores. Y en el minuto 2:52 se pregunta: “Which end is nearer to the ultimate creator, if I may use a religious metaphor? Which end is nearer to God? Beauty and hope, or the fundamental laws? I think that the right way, of course, is to say that the whole structural interconnection of the thing is what we have to look at. [...] And so I do not think either end is nearer to God. To stand at either end, and to walk off that end of the pier only, hoping that out in that direction is the complete understanding, is a mistake.” (“¿Qué extremo está más cerca del creador final, si puedo usar una metáfora religiosa? ¿Qué extremo está más cerca de Dios? ¿La belleza y la esperanza, o las leyes fundamentales? Creo que la respuesta correcta, por supuesto, es decir que lo que debemos mirar es la interconexión completa de las cosas. [...] Y entonces no creo que ninguno de los dos extremos esté más cerca de Dios. Pararse en cualquier extremo y caminar solo por ese extremo del muelle, esperando que partiendo desde ese punto encontraremos el entendimiento completo, es un error.”).

En términos más contemporáneos, y como dije hoy, los sistemas físicos extensos son como los ogros. Y los ogros son como las cebollas. ¿Apestan? ¡No! ¿Te hacen llorar? ¡No! ¿Si los dejás al sol se vuelven marrones y les crecen pelitos blancos? ¡Tampoco! Las cebollas tienen capas. Los ogros tiene capas. Y los sistemas físicos extensos tienen capas, como los ogros y las cebollas.

Y como los ogros, los sistemas físicos extensos no pueden comprenderse si solo miramos las capas más externas, o si solo miramos las capas centrales. Es la capacidad de mirar el conjunto lo que hace que dejemos de ser tan burros y podamos entender a los ogros.

En esta materia nos interesan los sistemas extensos, para los que estamos haciendo (y vamos a tener que hacer) muchas aproximaciones. La elección de qué aproximaciones son razonables, y cuales no, serán el resultado de observar la naturaleza. No espero que respondamos la pregunta de Feynmann sobre qué extremo está más cerca de la verdad última, pero sí espero que podamos encontrar interés en estudiar ambos extremos de las jerarquías de los sistemas físicos. Y que aprendamos que los sistemas físicos complejos muchas veces no pueden ser reducidos a ecuaciones en términos de las leyes fundamentales de la física. Pero que, sin embargo, lo que aprendimos hasta ahora sobre las leyes fundamentales y sobre sistemas sencillos nos pueden ayudar a comprender mejor a los sistemas complejos. Porque no siempre podemos obtener lo que queremos, pero si lo intentamos, podemos encontrar lo que necesitamos.

De yapa, otro video de Feynman hablando de ciencia, el calor, la temperatura, y muchas cosas más:

“Este pensador observó que todos los libros, por diversos que sean, constan de elementos iguales: el espacio, el punto, la coma, las veintidós letras del alfabeto. También alegó un hecho que todos los viajeros han confirmado: No hay en la vasta Biblioteca, dos libros idénticos. De esas premisas incontrovertibles dedujo que la Biblioteca es total y que sus anaqueles registran todas las posibles combinaciones de los veintitantos símbolos ortográficos (número, aunque vastísimo, no infinito) o sea todo lo que es dable expresar: en todos los idiomas. Todo: la historia minuciosa del porvenir, las autobiografías de los arcángeles, el catálogo fiel de la Biblioteca, miles y miles de catálogos falsos, la demostración de la falacia de esos catálogos, la demostración de la falacia del catálogo verdadero, el evangelio gnóstico de Basilides, el comentario de ese evangelio, el comentario del comentario de ese evangelio, la relación verídica de tu muerte, la versión de cada libro a todas las lenguas, las interpolaciones de cada libro en todos los libros, el tratado que Beda pudo escribir (y no escribió) sobre la mitología de los sajones, los libros perdidos de Tácito.”

Jorge Luis Borges, La Biblioteca de Babel (1941).

¿De cuántas formas pueden reordenarse los veintitantos símbolos ortográficos de la Biblioteca de Babel? ¿De cuántas formas puede Christopher Nolan reordenar el argumento de sus películas para hacer una película nueva? (de ser posible, que todavía se entienda). ¿Y cuanta información quedará en la película más arrevesada que Christopher Nolan pueda dirigir? Como suele ocurrir, los Simpsons se preguntaron todo esto antes (¡pero no antes que Borges o que Claude Shannon!):

¿Cuál es la relación entre entropía e información? En 1949, ocho años después que Borges publicase La Biblioteca de Babel, Claude Shannon publicó un trabajo en el que introdujo su famoso concepto de entropía de la información,

S = – Σ p_i log p_i.

En ese trabajo, aunque presentó una serie de teoremas con motivaciones plausibles, Shannon acepta que su principal motivación para usar una definición de este tipo, y en particular la función logaritmo, tiene que ver con que es práctica para lidiar con magnitudes medidas que pueden variar en varios órdenes de magnitud, con que vuelve ciertas operaciones con números grandes más fáciles de manejar, y con resultados previos en mecánica estadística como las definiciones de entropía de Boltzmann y de Gibbs. Shannon usó log₂, pero nosotros usamos el logaritmo natural porque es más natural para nuestra materia. En clase vimos cómo esta definición se relaciona con nociones de desorden o de interteza, y que para sucesos equiprobables se reduce a S = log(N), donde N es el número de sucesos posibles. Pero ¿cómo se relaciona esto con la noción de información?

Llamativamente, Borges se adelantó en su Biblioteca de Babel a esta pregunta. En otra parte del cuento escribe:

“El número de símbolos ortográficos es veinticinco. Esa comprobación permitió, hace trescientos años, formular una teoría general de la Biblioteca y resolver satisfactoriamente el problema que ninguna conjetura había descifrado: la naturaleza informe y caótica de casi todos los libros. Uno, que mi padre vio en un hexágono del circuito quince noventa y cuatro, constaba de las letras MCV perversamente repetidas desde el renglón primero hasta el último. Otro (muy consultado en esta zona) es un mero laberinto de letras, pero la página penúltima dice «Oh tiempo tus pirámides».”

Imaginemos, como Borges, un conjunto de símbolos ortográficos formado por 22 letras del alfabeto, mas el punto, la coma y el espacio (que marcaremos como “_”):

ABCDEFGHIKLMNOPQRSTVYZ.,_

Pensemos ahora que tenemos diferentes “emisores” que transmiten un mensaje usando estos símbolos. Como en el video de Los Simpsons (en un tema que está íntimamente relacionado con el cuento de Borges y el concepto de entropía de Shannon), pensemos que tenemos monos encadenados a máquinas de escribir, y que pueden escribir al azar textos de 50 símbolos en cada mensaje:

1. El primer mono (M₁) aprieta la letra A todas las veces: “AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA”.
2. El segundo mono (M₂) aprieta solo letras con equiprobabilidad, sin usar puntuación o espacios: “AYZTMOICPQERVILVVLMODNBEKSDEHGAHGALMKEYC”
3. El tercer mono (M₃) aprieta cualquiera de las 25 teclas con equiprobabilidad: “DH, EKHVOZ . EZVIASC B PIM,YICAK DELA.ALSFBZOQNY E”.
4. El cuarto mono (M₄) aprieta cualquier tecla con su probabilidad de uso en el español (por ejemplo, el espacio tiene una probabilidad de ocurrencia de ≈ 0.17, la letra “A” de ≈ 0.10, la “E” de ≈ 0.11, etc.): “EOS RILND . QNL PAE A ARDTEOS DCMAEE AMA”.
5. El quinto mono (M₅) tiene un vocabulario de 10 palabras, y usa las reglas de espaciado y puntuación del español. Su vocabulario es: CASA, PEPE, TUS, PESCA, EN, PIRAMIDES, DOS, OH, PARA y TIEMPO. Usando solo esas palabras al azar, y el punto, la coma y el espacio, escribe: “DOS PESCA. TUS CASA PEPE, OH TIEMPO TUS PIRAMIDES.”

¿Cuánta información hay en cada mensaje? Para contestar esto, preguntémonos para qué emisor es más difícil predecir la ocurrencia de la siguiente letra, si nos llegasen sus mensajes de a una letra por vez (por ejemplo, por un telégrafo). En el primer caso, una vez que reconocimos el patrón, es fácil saber que la siguiente letra será una A. Cada nueva A no agrega entonces más información que la que ya teníamos (¡ya sabíamos que nos llegaría una A!). Es fácil también ver que el caso más difícil para predecir la ocurrencia de una nueva letra corresponde al del mono M₃. Por otro lado, el mensaje de M₅ parece más complicado, pero luego de recibir las letras “PES”, sabemos que solo pueden estar seguidas por “CA”. La entropía de Shannon mide esta noción de información, basada en la idea de que cuanto más difícil sea predecir la siguiente letra, más información nos aporta conocerla. Calculemos la entropía de cada emisor:

1. S₁ = ln 1 = 0
2. S₂ = ln 22 ≈ 3.091
3. S₃ = ln 25 ≈ 3.219
4. S₄ = -Σ p_i log p_i ≈ 2.766
5. La entropía S₅ es más difícil de calcular, pero es menor a S₄ y mayor a S₁.

Hay otra forma interesante de pensar cuánta información genera el emisor, y es pensar cuánto podemos comprimir el mensaje que nos envía el emisor sin perder información. Para el primer mono nos alcanza con decir que envió 50 “A”. El mensaje de M₅ lo podemos comprimir como “D PES. TU C PEP, O TI TU PIR.” (ya que “D” solo puede ser seguido por “OS”, “PES” por “CA”, “TU” por “S”, etc.). En el mensaje de M₃ no podemos sacar nada sin perder información. Un teorema famoso de Shannon nos dice que (para mensajes muy largos) la cota máxima a cuánto podemos comprimir el mensaje de un emisor sin perder información está relacionada con su entropía.

Los que quieran saber más pueden leer el paper original de Shannon:

• A mathematical theory of communication

Me imagino que todos quieren ser millonarios. ¡Pero seguro nunca se imaginaron que esta materia era la forma de alcanzar sus deseos! Salvo, obviamente, que hayan visto The hangover (2009), o películas un poco más serias como Rain Man (1988) y 21 (2008) (ambas basadas, con diversas libertades narrativas, en historias reales). En las últimas clases comenzamos a estudiar probabilidades. Los temas que vimos se pueden usar para ganar en juegos de azar (¡o mejor aún, para evitarlos!), y para ilustrar cómo les cuento dos historias. Pero antes de leer estas historias no dejen de ver un espectacular Google Colab con problemas de probabilidad y estadística de la guía que hizo Cecilia Fossa Olandini, una docente auxiliar de la materia hace unos años (el notebook incluye la solución numérica al problema de Monty Hall, el concurso de televisión que mencioné brevemente en clase y del que volveremos a hablar más adelante).

La primer historia es la del método para ganar en la ruleta de Edward Thorp (también creador de métodos para contar cartas en el blackjack) y Claude Shannon (si, el mismo Shannon de la entropía que veremos repetidas veces en la materia). Todos los juegos de azar en los casinos tienen esperanza negativa: si siguen jugando, a la larga solo pueden perder. En el caso de la ruleta, esto está relacionado con que un pleno (acertar a un número) paga 35 veces la apuesta, pero la probabilidad de acertar el número es 1/37 (pues la ruleta tiene 36 números más el cero). Así, en promedio, cada vez que apuestan pierden. El desafío es convertir la esperanza en positiva, es decir, saber con probabilidad mayor a 1/35 qué número va a salir. En los siguientes artículos Edward Thorp explica en detalle diversos métodos para ganar en la ruleta:

• Sistemas para la ruleta I
• Predicción física de la ruleta I

Los que quieran mas información sobre juegos de azar (y las siguientes entregas de estos artículos) pueden mirar la página web de Edward Thorp.

Básicamente existen tres tipos de métodos para la ruleta: (1) métodos matemáticos, (2) métodos basados en desperfectos de la ruleta, y (3) métodos predictivos basados en la física de la ruleta. Los primeros no son viables, ya que como mencioné arriba, los juegos de casino están diseñados para tener esperanza negativa. Al segundo método vamos a volver en un rato. El tercer camino es el que eligieron Thorp y Shannon.

En 1960 Thorp y Shannon usaron el hecho de que en los casinos se puede seguir apostando mientras la ruleta gira (y hasta que el crupier grita “¡No va más!”) para crear un algoritmo que basado en la velocidad de rotación de la ruleta, la velocidad de la bola, y su posición inicial aproximada (estimadas contando solo con inspección visual el número de vueltas que la ruleta y la bola dan en un período corto de tiempo), predice estadísticamente en qué octante de la ruleta puede caer la bola. En espíritu (aunque no en los detalles) esto es parecido a lo que vimos en el problema del camino al azar: no podemos saber dónde terminará la bola, pero nos alcanza con conocer la zona más probable de la ruleta en la que la bola puede terminar. Con esta información extra, la esperanza se vuelve positiva para el apostador. Pueden encontrar un artículo de divulgación con esta historia aquí:

• Artículo sobre Edward Thorp en Engadget

Para realizar predicciones rápidas en el casino, Thorp y Shannon armaron una computadora pequeña, del tamaño de un atado de cigarrillos, que se llevaba con una faja en la cintura y se conectaba al zapato para ingresar los datos pisando fuerte o moviendo los dedos del pie. La siguiente foto muestra la pequeña computadora de Thorp y Shannon (la que se llevaba en la cintura):

Otra persona (el apostador) usaba un pequeño receptor y un auricular para obtener la predicción y realizar rápidamente una apuesta. En la práctica, y para evitar ser detectados usaban a tres personas: una que medía, otra que llevaba la computadora, y el tercero que realizaba la apuesta, todos conectados por un sistema de radio:

¡Lo mas interesante es que el método funciona! Thorp y Shannon lo usaron con cierto éxito en Las Vegas. Una década más tarde un grupo de estudiantes de California perfeccionaría el sistema reduciendo aún más las computadoras y escondiéndolas completamente en zapatos (aquí pueden ver una imagen de las computadoras y encontrar algunos detalles sobre cómo funcionaban; el apostador ingresaba el período de rotación de la ruleta y el de la bola apretando un pulsador con el dedo del pie, y en otro zapato otra computadora devolvía la predicción del octante en el que caería la bola con una vibración). Todo esto además terminó siendo usado para el guión de un episodio de la serie original de Misión Imposible (1966), con un título insuperable:

• Odds on evil

La segunda historia tiene que ver con el segundo método para ganar en la ruleta, basado en desperfectos de la ruleta, e involucra a un estudiante de doctorado de Richard Feynman. Alrededor de 1940, Albert Hibbs y Roy Walford acumularon datos de jugadas en casinos de Reno y Las Vegas, para identificar algún pequeño bias o desperfecto en las ruedas de ruleta que favoreciera estadísticamente a ciertos números. Usando los datos estadísticos obtenidos para cada ruleta, Hibbs y Walford ganaron 8300 dólares en un día (las ruletas actuales no tienen este nivel de imperfección, por lo que lamentablemente el método no es aplicable hoy). Pueden leer una historia sobre Hibbs y Walford aquí:

• El método de Hibbs y Walford

Espero haberlos convencido, con estas historias, de que lo más conveniente es no apostar (salvo que uno esté dispuesto a esconder una computadora en un zapato). Para mostrar que más de 4000 físicos llegaron a la misma conclusión, les dejo un link a la famosa historia de la convención de físicos en Las Vegas que dió origen a la frase “They each brought one shirt and a ten-dollar bill, and changed neither”:

• Cómo 4000 físicos le dieron a un casino de Las Vegas su peor semana

Voy a contarles la historia de cómo John Snow aplicó la estadística en medicina, y cómo nos podría haber salvardo a todos del coronavirus. En 1854 John Snow salvó a Londres de un brote de cólera usando la estadística. ¿Pensaron que este posteo iba a ser sobre Jon Snow y Game of Thrones, o sobre House of the Dragon? ¿O sobre Elden Ring, guionado por el mismísimo G.R.R. Martin? Lo siento. Y va a ser aún mas aburrido, porque el Snow de esta historia no se revolcaba en la cama con aspirantes al trono de hierro. Pero el verdadero John Snow no solo salvó a Londres con la estadística, sino que por ese motivo es también considerado uno de los padres de la epidemiología moderna.

En esa época se pensaba que el cólera se transmitía por “miasmas” en el aire, que eran emitidos por material en descomposición y que enfermaban a quienes los respiraban. John Snow era médico en el Soho, y cuando se desató un brote de cólera desconfió de esta explicación. Sus vecinos y otros médicos lo acusaban de no saber nada (“You know nothing, John Snow”), así que John Snow hizo el siguiente mapa con los casos de cólera que veía en el barrio:

Las barras negras son histogramas, y muestran el número de casos de cólera por casa (que están sospechosamente distribuidos en forma preferencial alrededor de un punto). Snow también hizo estudios “doble ciego” usando la información de que algunas casas usaban agua de una compañía y otras casas eran provistas con agua de otra empresa (y el número de enfermos en esas casas resultó ser diferente). Con estos datos, Snow concluyó que el cólera se debía contagiar por algún agente en el agua (Pasteur introduciría la idea de los gérmenes recién siete años después), e identificó a la posible fuente de agua contaminada como una bomba de agua en la esquina de Broad Street y Cambridge Street (que, efectivamente, había entrado en contacto con un pozo ciego). Los interesados pueden leer mas detalles sobre esta historia acá.

A fines prácticos, lo que nos importa es que John Snow realizó un experimento luego de identificar dicha bomba de agua para verificar su teoría: ordenó que remuevan la manija de la bomba, de forma tal que no se pudiera usar más. Y el número de casos de cólera disminuyó. Hoy en Londres, en el lugar donde se encontraba aquella bomba, está instalada una réplica (¡sin manija!) con una placa que recuerda los sucesos:

En el día de hoy la mecánica estadística se usa activamente para entender epidemias. Y también se usan modelos estocásticos similares al modelo de camino al azar que vimos en clase (aunque en el caso de epidemiología, suelen tener muchas más variables aleatorias). Los modelos más sencillos de epidemias tienen “compartimientos” (para individuos Susceptibles, Infectados y Recuperados, o SIR). Es decir, los números de individuos susceptibles (S), de individuos infectados (I) y de individuos recuperados (R) varían en cada paso (con el avance de los días) como variables aleatorias con alguna distribución de probabilidad conocida:

En estas ecuaciones, B(t) es una función de distribución (conocida) de la probabilidad de que un individuo susceptible se infecte en el tiempo t. Noten que cuando esto ocurre, el número de individuos susceptibles S disminuye, y el número de infectados I crece (t + Δ corresponde al tiempo luego de realizar un paso, por ejemplo, un día más tarde que el tiempo inicial t). De la misma forma, C(t) es una función de distribución, también conocida, de la probabilidad de que un individuo infectado se recupere. El número de individuos recuperados, R, se obtiene simplemente de pedir que la población total N no cambie en el tiempo. Noten cómo, a semejanza del modelo de camino al azar, contamos con algunas distribuciones de probabilidad conocidas (B y C, que describen propiedades de la enfermedad, equivalentes a la distribución de probabilidad f que vimos en clase), y el modelo nos permite calcular cantidades “macroscópicas” (la función de distribución de probabildad p): el número de infectados o de recuperados en una sociedad.

Partiendo de este modelo muy sencillo pueden construirse modelos más complejos (por ejemplo, con más “compartimientos” para considerar diferentes estadios de una enfermedad, para considerar poblaciones con diferentes edades, para considerar fallecimientos, o para considerar diferentes regiones de una ciudad o un país).

Este tipo de modelos, en el límite termodinámico tienden a ecuaciones diferenciales (más adelante también veremos cómo se obtiene el límite termodinámico de sistemas aleatorios) que describen cualitativamente la evolución de epidemias en poblaciones grandes. En los últimos años, y especialmente durante la epidemia de coronavirus, todo el mundo habló de estos modelos. Los que quieran saber más sobre modelos epidemiológicos pueden ver esta página, o leer este capítulo de un libro. El capítulo del libro tiene una discusión interesante sobre las limitaciones de los modelos (limitaciones que muchas personas olvidaron), y sobre qué condiciones se necesitan para poder alcanzar la inmunidad de rebaño en forma natural o al introducir vacunas (esto no siempre ocurre). O pueden ver un trabajo que realicé con otros investigadores del Departamento de Física aplicado al caso particular de la transmisión de COVID-19 en la ciudad de Buenos Aires, o mirar un resumen de ese trabajo en este video.

Y los que se quedaron con ganas de Juego de Tronos pero se aburrieron con House of the Dragon, pueden seguir este link (aunque el link contiene lenguaje vulgar, y debido a su contenido, nadie debería verlo).

¿Qué puede ser más sencillo que la física de una bolsa arrastrada por el viento? ¿O de un grano de polen sumergido en agua en reposo? Como aprendieron Robert Brown, Albert Einstein y Marian Smoluchowski a mediados del siglo XIX y principios del siglo XX, a veces hay tanta belleza en el mundo que no puede explicarse en forma sencilla.

La física de partículas sumergidas en fluidos, aunque en una primera impresión puede parecer sencilla, ha jugado un papel central en el desarrollo de la mecánica estadística y en nuestra comprensión actual de sistemas en equilibrio termodinámico (y también de sistemas que están fuera de equilibrio). El movimiento browniano fue descrito por primera vez por Robert Brown en 1827, mientras observaba un grano de polen sumergido en agua en el microscopio. Brown notó que el grano de polen parecía moverse y sacudirse al azar, sin ninguna razón aparente.

A principios del siglo XX, Einstein y Smoluchowski explicaron este fenómeno asumiendo que el choque de las moléculas de agua con el grano de polen producían el movimiento de la partícula observado en el microscopio. Esto permitió verificar en forma indirecta la existencia de átomos y moléculas en experimentos. Pero el movimiento browniano, y las teorías de Einstein y Smoluchowski, marcaron también el camino para el estudio de procesos de difusión y de los procesos aleatorios. Y las partículas sumergidas en fluidos siguen dando sorpresas aún hoy. Muy recientemente, experimentos usaron partículas coloidales sumergidas en líquidos para verificar una relación para las fluctuaciones en sistemas fuera del equilibrio termodinámico conocida como la igualdad de Jarzynski (una igualdad que nos dice que en sistemas fuera del equilibrio la entropía puede disminuir, pero que la probabilidad de que esto ocurra es mucho menor que la probabilidad de que la entropía aumente; más adelante vamos a volver sobre este tema en otro posteo). Y un sistema similar se usó para verificar una predicción de Landauer de 1961, que dice que borrar información tiene un costo termodinámico: cada vez que se borra información debe realizarse una cantidad mínima de trabajo, aumentando inevitablemente la entropía del sistema (otro tema sobre el que volveremos más adelante).

En otras palabras, un tema que parece sencillo, como el estudio de una partícula sumergida en un líquido macroscópicamente en reposo, es mucho más complicado de lo que parece. Y para describirlo se han construido modelos físicos y matemáticos con diferente grado de complejidad.

El modelo de camino al azar unidimensional discreto es un modelo muy simplificado para el fenómeno del movimiento browniano. En este modelo, en cada paso una partícula solo puede moverse  con alguna probabilidad a la derecha o a la izquierda, con pasos discretos en el espacio y el tiempo. El límite continuo, en múltiples dimensiones espaciales, se encuentra más cerca del movimiento browniano. Pero dada la ubicuidad en la física del fenómeno del movimiento browniano, aún los modelos de camino al azar más sencillos encuentran múltiples aplicaciones, a veces en lugares tan inesperados como el estudio del crecimiento aleatorio de interfaces, el estudio de procesos de difusión en el océano (pueden encontrar en este link una aplicación a este tipo de problemas realizada por nuestro grupo de investigación), o en epidemiología (como veremos en un próximo posteo). En matemática el camino al azar también juega un rol importante a la hora de estudiar procesos estocásticos (Pablo Groisman, @pgroisma, en el Departamento de Matemática trabaja, entre otras cosas, en estos temas).

En física, un resultado importante de los modelos de camino al azar, y de la teoría de Einstein y Smoluchowski para el movimiento browniano, es la predicción de que el desplazamiento cuadrático medio de las partículas crece como la raíz del número de pasos (o del tiempo). El siguiente gráfico muestra 100 caminos al azar simétricos, y la predicción para el desplazamiento cuadrático medio:

Este resultado permite calcular el coeficiente de difusión para el sistema. Pero aunque parezca sencillo, este tampoco es un resultado trivial. Un coeficiente de difusión es una magnitud macroscópica (como la viscosidad de un líquido, o la conductividad eléctrica de un conductor), pero en este ejemplo el coeficiente macroscópico emerge como resultado de promediar sobre la trayectoria de muchas partículas individuales (y microscópicas). A lo largo de la materia veremos formas sistemáticas para calcular coeficientes efectivos de esta forma.

El título de este post (además de hacer referencia a una mala película con buena música), hace referencia a dos temas que discutimos en clase: energía libre y formación de nubes (pero de gotas de agua, no de albóndigas).

El concepto de energía libre juega un rol muy importante en física atmosférica. Y quién estableció su importancia fue Edward Lorenz (¡el del atractor de Lorenz y la teoría del caos!). Lorenz es conocido por su atractor caótico. Es menos sabido que derivó sus ecuaciones a partir de las ecuaciones físicas que describen la convección en la atmósfera, es decir, el movimiento del aire que transfiere calor desde el suelo más caliente hacia las capas más altas (y más frías) de la atmósfera. Una de las propiedades de los sistemas caóticos es que tienen sensibilidad a las condiciones iniciales: pequeños cambios en el estado del sistema son amplificados rápidamente, resultando en grandes cambios un corto tiempo después. La pregunta “¿Puede el aleteo de una mariposa en Brasil desencadenar un tornado en Texas?” es de uno de los trabajos de Lorenz sobre predictibilidad atmosférica. Lorenz puso límites estrictos a la cantidad de días en los que podemos predecir el estado del tiempo. Pero Lorenz hizo más contribuciones a la física atmosférica y a las ciencias de la atmósfera, y ciertamente una no fue la de construir una máquina para que lluevan hamburguesas.

La contribución de Lorenz que nos interesa por su vínculo con los temas que vimos en clase es el uso de la termodinámica para establecer el ciclo energético de la circulación global de la atmósfera, definir la “energía potencial disponible”, y explicar por qué solo el 2% de la energía que llega del sol se convierte en movimiento del aire en forma de vientos medios. La “energía potencial disponible” de Lorenz es una aplicación muy elegante y importante de la termodinámica: permite calcular cuanta energía almacenada en la atmósfera puede usarse para hacer trabajo, y generar vientos o tormentas.

La región más baja de la atmósfera, llamada la tropósfera y donde ocurren los fenómenos del tiempo que afectan nuestras vidas todos los días, muestra una circulación global (un “viento medio”) persistente en el tiempo:

Como pueden ver, los vientos en la superficie de la Tierra cerca del ecuador apuntan preferencialmente en la dirección este-oeste, mientras que en las latitudes donde se encuentra Buenos Aires y en la región patagónica apuntan usualmente en la dirección opuesta (aunque en el caso particular de la región de Buenos Aires, los vientos medios suelen estar afectados por un conjunto de centros de alta y baja presión que cambian ligeramente con las estaciones).

El movimiento medio de la atmósfera causado por esta circulación global tiene asociada una energía cinética (de la misma forma que una tormenta involucra también una cantidad importante de energía cinética asociada al movimiento de la masa de aire). ¿Pero cuál es la fuente de esa energía? La fuente de energía es la radiación solar, que es absorbida por el suelo, y reemitida en forma de calor. El ciclo completo (tomado de un paper de Edward Lorenz que cito más abajo) es el siguiente:

La energía (en forma de calor) liberada por el suelo se convierte en energía potencial (gravitatoria, asociada a la estratificación del aire) y energía interna (o energía térmica del gas). Luego, mediante una conversión adiabática, esa energía potencial se convierte en movimiento (por ejemplo, por diferencias de temperatura y presión en diferentes lugares, que resultan en la aparición del viento que intenta reestablecer el balance de presión). Esa energía se disipa por fricción, y una parte vuelve a calentar el suelo, lo que junto con nueva radiación solar incidente reinicia el ciclo.

Sin embargo, solo una fracción muy pequeña de la energía incidente (como mencioné anteriormente, cerca del 0.02 de la energía total en la radiación solar) se puede convertir en trabajo y sostener la circulación global de la atmósfera contra la disipación. Lorenz se dio cuenta que era incorrecto asumir que toda la energía disponible podía convertirse en trabajo, y que una estimación termodinámicamente correcta debía involucrar a una energía libre (porque bajo las condiciones correctas, la energía libre acota la máxima energía que puede convertirse en trabajo, según el segundo principio de la termodinámica). Así, Lorenz definió la “energía potencial disponible“, que es la forma moderna de cuantificar la energía disponible para hacer trabajo en la atmósfera.

Para los que quieran leer un poco más sobre estos temas, les dejo tres links:

• Un link a un coloquio de Edward Lorenz, donde explica el uso del concepto de energía libre para estimar cuán intensa puede ser la circulación global en la atmósfera. No es el objetivo que entiendan los detalles, solo que (si están interesados) miren la introducción para ver cómo usa conceptos termodinámicos y ciclos energéticos para definir la energía potencial disponible para hacer trabajo.
• Un link a un artículo sobre un laboratorio que estudia formación de gotas en nubes, y su suspensión por la convexión en la nube (¡con un video promocional!). Entre otras cosas, el artículo menciona el rol de partículas pequeñas suspendidas en el aire (aerosoles) para que se generen las gotas, algo que yo mencioné brevemente en clase.
• Los interesados en nubes y gotas de lluvia también pueden ver este trabajo que nuestro grupo de investigación publicó un par de años atrás en Physical Review Letters sobre por qué las gotas de lluvia caen más rápido que lo que deberían.