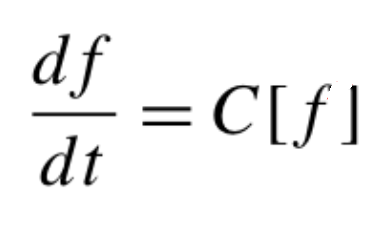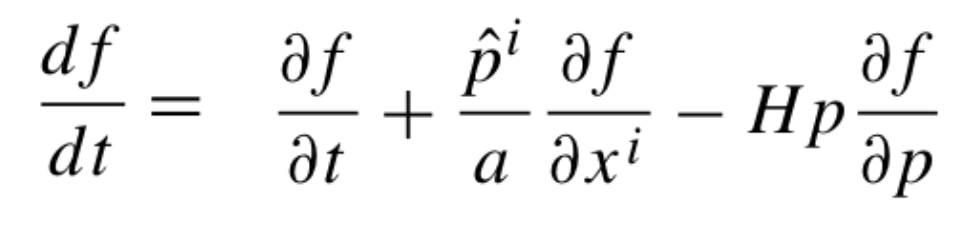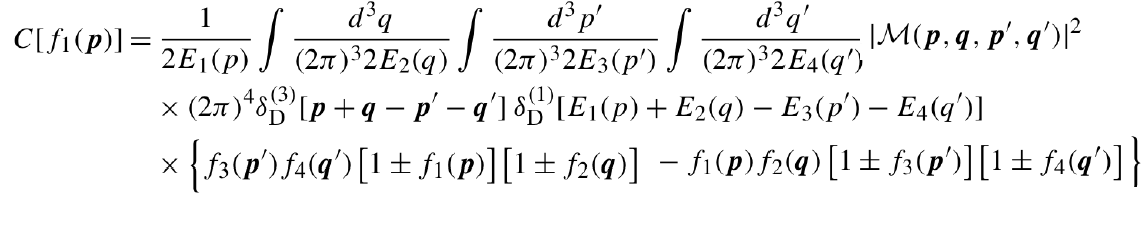Además de ser un área de la física que, con el devenir de la relatividad general pudo hacer predicciones muy robustas, y con el avance de la tecnología pudo lograr mediciones muy precisas, la cosmología tiene otra gran virtud: el marketing, reflejado en los exageradamente buenos nombres que les ponen a los descubrimientos.
La nucleosíntesis primordial (o BBN, por “big bang nucleosynthesis”, elijan el nombre que les guste más) parece el nombre del ataque de un pokemón (uno groso, de esos que tienen 150 de potencia y un turno de descanso). Pero que el nombre llamativo no los deje engañar: es una de las predicciones más precisas que tiene la cosmología respecto del universo temprano (muy temprano, se estima que BBN ocurrió entre que el universo tenía 10 y 10^3 segundos).
Como su nombre lo indica, BBN representa la formación de núcleos atómicos en el universo temprano. Conceptualmente, se podría pensar que cuando el universo estaba muy caliente, los fotones tenían mucha energía. En ese momento, si un protón quería juntarse con un neutrón para formar un núcleo de Deuterio, los fotones existentes inmediatamente destruían este núcleo. Sin embargo, como a medida de que el universo se expande, su temperatura disminuye, llega un momento en que los fotones ya no pueden destruir tan fácilmente a estos estados ligados. En ese momento, comienzan a formarse núcleos, por ejemplo de Deuterio.
Los núcleos de Deuterio, a su vez, pueden juntarse para formar núcleos más pesados, como por ejemplo núcleos de Tritio o Helio 3. Luego de estos núcleos, viene la estrella: durante la época de BBN, y cuando hay suficiente Deuterio en el universo, se forman núcleos de Helio 4. Estos núcleos son particulares, porque se entiende bien como se producen en estrellas, lo curioso, es que cuando se midió la abundancia relativa de Helio 4 en el universo, está dio significativamente mayor que la que podría haberse formado por producción estelar. ¿La respuesta? El excedente era Helio 4 primordial, formado durante la época de BBN en el universo temprano.
Pero… ¿Cómo se puede calcular la abundancia relativa de Helio 4 durante la época de BBN? ¡Claro! Con la ecuación de Boltzmann (en relatividad general). La ecuación se escribe de una forma muy amigable:
Donde la derivada total se escribe teniendo en cuenta la dinámica del espacio-tiempo del universo (representada por ejemplo en H, que es el parámetro de Hubble):
Y aquí viene lo bueno, jóvenes, el querido y amado término de colisiones:
En casos de equilibrio, la ecuación se simplifica bastante y se obtiene la ecuación de Saha. Con esta ecuación se pueden hacer estimaciones rápidas de como evolucionan algunas especies, tales como los neutrones o los electrones.
Volviendo a lo que nos atiende, para cada proceso que consideremos hay una ecuación de Boltzmann. Por ejemplo, algunos de los procesos que nos interesan son:
p+n <—> D+fotón , D+D <—> ^3He+p , D+^3He <—>^4He+n
La cuestión es que para cada proceso hay una ecuación de Boltzmann como las que mostramos arriba. Para poder predecir la abundancia de Helio 4 primordial, hay que escribir las ecuaciones de Boltzmann de todos los procesos relevantes y resolverlas a la vez, dado que están acopladas. Existen códigos numéricos que hacen estos cálculos, obteniendo una abundancia relativa de Helio 4 de aproximadamente 23% (más menos un porciento). Las mediciones dependen del modelo estelar que se empleé, pero la abundancia relativa inferida es de aproximadamente del 24%, siendo esta una predicción muy fuerte del modelo de cosmología LCDM.
Así que ya saben, aunque la guía de Boltzmann sea cortita, y probablemente no entre en el parcial, es un tema relevante que se usa actualmente en varias áreas de la física.