En este post les dejo un video que me parece una demostracion contundente y super divertida del efecto Magnus que vimos en la ultima clase teorica.

Espero que les sea util (y divertido)!

Aqui el video:

Les dejo aqui el apunte que me pidieron en clase sobre el método de Milne-Thomson para el calculo de funciones holomorfas a partir de sus componentes reales y/o imaginarias. En el documento les muestro la forma general del metodo, asi como su aplicacion a un flujo que vimos en clases teoricas.

El documento podran descargarlo haciendo click aqui.

Espero que les resulte util.

Me parece interesante comentarles brevemente en este post cómo es posible obtener y visualizar flujos potenciales bidimensionales (como los que venimos discutiendo las ultimas clases de teoricas) en el laboratorio.

Un montaje experimental comúnmente utilizado para producir y estudiar flujos potenciales bidimensionales es la celda de Hele-Shaw, introducida hace más de 100 años por Henry Hele-Shaw. Una celda de Hele-Shaw consiste esencialmente en el flujo de un líquido viscoso entre dos placas plano-paralelas ligeramente separadas entre sí.

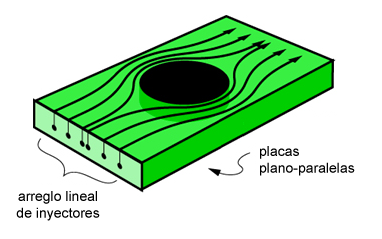
La figura muestra un esquema simple de una celda de Hele-Shaw, ilustrando el flujo en torno de un obstáculo; un arreglo lineal para la inyección de colorante (como trazador) y algunas líneas de corriente a modo de visualización. El flujo dentro de la celda, laminar y paralelo, se conoce como flujo de Poiseuille plano y será objeto de estudio en la segunda mitad de la materia (en el marco de la guía de flujos viscosos).

Una propiedad paradójica de la celda de Hele-Shaw es que, a pesar de que el flujo es viscoso, las líneas de corriente bidimensionales que se observan tienen las propiedades de un flujo potencial. No se alarmen: más adelante en el curso veremos en detalle cómo probar esta afirmación.

Les dejo además un video que muestra el dispositivo experimental de Hele-Shaw y su operación. El obstáculo empleado (un cilindro en este caso) es ubicado en el pequeño espacio entre dos placas de vidrio dispuestas verticalmente. Un fluido viscoso y transparente se carga en un reservorio sobre la celda y se lo deja fluir a través de ella bajo la acción de la gravedad. El dispositivo cuenta además (como es usual) con un arreglo lineal de inyectores equiespaciados por donde se hace ingresar un fluido coloreado de iguales características (viscosidad, densidad, etc.). El reservorio se mantiene continuamente alimentado con fluido transparente y la visualización comienza haciendo ingresar el trazador al sistema. Para incrementar el contraste de las líneas observadas, se suele emplear un trazador fluorescente y trabajar a oscuras iluminando únicamente el flujo en la celda. Pueden visualizar el video haciendo click sobre la imagen asociada.

Finalmente, les dejo dos videos más: dos visualizaciones experimentales de las líneas de corriente de un flujo potencial bidimensional uniforme que enfrenta (a) un obstáculo cilíndrico y (b) un perfil alar; ambas obtenidas con la celda de Hele-Shaw mostrada en el primer video.

Espero que les sea util.

Les dejo en este post el link a una notebook de IPython que prepare en la que les describo cómo calcular la función corriente, así como el potencial complejo, en un caso con una fuente de caudal y un vortice. Encontrarán además dos adicionales: (a) la forma de las líneas de corriente para el caso general, y (b) un caso en el cuál se observa en la naturaleza este tipo de flujo.

Este caso es de interés por dos razones. Por un lado, el ejemplo sirve como ilustración del método general para el cálculo del potencial complejo de un flujo singular (i.e., que incluye singularidades). Por el otro, vemos que calculamos, como les comente en clase, el potencial complejo para los dos ‘ladrillos fundamentales’ de los que están constituidos todos los flujos que consideraremos en esta práctica: una fuente isótropa de caudal constante y un vórtice (dos casos límite que surgen de lo expuesto en este documento).

Cualquier flujo que resulte combinación de ellos (p.ej., dipolos) podrá calcularse fácilmente (segun les describo en detalle en el documento que les adjunto) dado que las ecuaciones para la función potencial y la función corriente responden al principio de superposición.

Espero que les sirva.

En este post les comparto el link a una notebook de IPython que prepare para mostrarles cuan sencillo es tratar problemas simbolicos empleando la libreria ‘sympy’ de Python. Para ilustrar su uso, elegi el problema de determinar el campo de velocidades asociado a una fuente puntual de caudal constante frente a un plano infinito.

El objetivo es que puedan ver qué sencillo es manipular simbolicamente expresiones complejas (no solo complicadas!) con ipython gracias a sympy; ilustrando simultaneamente un flujo de interes.

Espero que les sea util.

En este post les dejo un notebook de Mathematica, en el cual les muestro cómo explotar la potencia de esta herramienta de cálculo simbólico (y numérico!) para resolver problemas de flujos potenciales bidimensionales.

En particular, el notebook trata un problema que veremos hoy en teoricas: el flujo alrededor de un cilindro con una circulación atrapada que enfrenta un flujo uniforme al infinito.

La idea detrás de este post es que tengan una guía de cómo resolver y analizar este ejercicio en Mathematica, teniendo en cuenta que ustedes conocen ya la física del problema. El propósito subyacente es que, si así lo desean, puedan extrapolar lo que aprendan aquí a la resolución de cualquier otro problema de la guía de trabajos practicos.

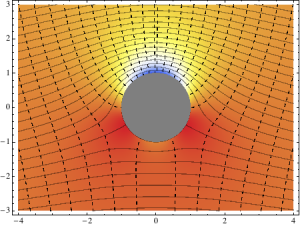
Curvas de nivel de la función corriente (trazo continuo), de potencial (líneas punteadas) y campo de presiones (en color) para un caso particular de los parámetros del problema.

Sólo a modo de sumario, les cuento qué tipo de cálculos aprenderán a hacer en Mathematica usando este notebook. Entre otras cosas, verán cómo: (i) definir un potencial complejo, (ii) aplicar el teorema del círculo de Milne-Thomson, (iii) determinar las funciones potencial y de corriente, (iv) calcular los campos de velocidad, (v) obtener el campo de presiones en todo punto del espacio usando el teorema de Bernoulli y (vi) calcular la fuerza sobre el obstáculo mediante: (a) la integral de presión sobre el contorno sólido y (b) el teorema de Blasius via el cálculo de residuos. Asimismo, podran ver como se representan usualmente en forma grafica cada uno de estos resultados y como generar dichos graficos en Mathematica.

El archivo/notebook de Mathematica podrán descargarlo (tanto en formato Mathematica como en formato PDF, para quienes no disponen del software) haciendo click derecho aquí y descomprimiendo el archivo .zip que descargaran.

Espero que les sirva.

En este post les propongo abordar un problema interesante relacionado con la aplicacion del teorema de conservacion de momento (en forma integral); en particular al calculo de fuerzas sobre un contorno solido con aplicaciones practicas importantes. En concreto, estaremos calculando la fuerza de anclaje necesaria para retener un stent en la aorta abdominal humana.

Un ‘stent’ medico es un dispositivo tubular metalico en forma de malla usualmente flexible, que tiene el proposito de ensanchar y/o mantener abiertos pasajes naturales del cuerpo que han sido ocluidos por alguna condicion medica (ver figura). La colocacion quirurgica de stents es una practica usual actualmente, por lo que existen stents arteriales, esofageos, biliares y ureterales, entre otros. La mayor parte de los stents son mantenidos en el lugar de colocacion por la presion de expansion que el mismo dispositivo ejerce contra la pared del pasaje donde es instalado. Sin embargo, en los ultimos años se han reportado casos de migracion de stents que debieron luego ser removidos quirurgicamente por presentar riesgos a la salud del paciente.

En este post les propongo calcular la fuerza que el flujo sanguineo ejerce sobre un stent ubicado en la aorta abdominal humana, a fin de explicar la migracion observada en pacientes y estimar la fuerza de anclaje necesaria para evitarla.

El enunciado completo de este problema adicional, asi como una resolucion sugerida, podran encontrarlo en esta notebook de Mathematica (para quien desee ejecutarla o editar el documento original) o bien en este documento PDF construido a partir de ella.

Les informamos que la reinscripción a las materias del Curso de Verano 2019 del Departamento de Física estará abierta desde el 11 al 18 de Febrero inclusive.

Esta es la última instancia para que se inscriban a la materia. Les recordamos que es responsabilidad de cada alumno la inscripción a las materias y por eso, recomendamos guardar el comprobante de inscripción a cada materia.

Espero que esta informacion les resulte util.

En este post les dejo un video asociado a la interpretacion fisica de la vorticidad, que espero  les permita comprender un poco mas qué es lo que la vorticidad mide. En el video podrán ver, luego de una breve introducción, el funcionamiento de un medidor de vorticidad ‘ideal’ (como el discutido en clase) pero llevado a la práctica con el mayor escrúpulo. Les recomiendo que vean únicamente los primeros 3’50, el resto del video es interesante también pero evoca conceptos que todavía no hemos visitado.

Espero que les sirva!

Nota: este video, denominado ‘Vorticity’, forma parte de una serie mucho más vasta filmada en los años 60′ en el MIT. Concretamente, en 1961 Ascher Shapiro fundó un organismo que dió en llamarse Comité Nacional para Films en Mecánica de Fluidos (National Committee for Fluid Mechanics Films, o NCFMF), y publicó una serie de 39 videos didácticos (junto con sus respectivos textos explicativos) que revolucionaron para siempre la enseñanza de la dinámica de fluidos a nivel universitario. Recientemente, el programa iFluids del MIT ha puesto un gran número de estos films a disposición del público en su sitio web. Aquellos interesados, podrán encontrar el resto de los videos (y los textos asociados) directamente en la página del NCFMF.  

En este post les dejo el link a un capitulo del libro de M. Guillen, “Five equations that changed the world”, acerca del desarrollo historico de lo que hoy conocemos como la ley de Bernoulli para los fluidos, que obtuvimos la ultima clase teorica y que emplearemos en las próximas clases en el marco de flujos potenciales planos.

En el texto, Michael Guillen nos cuenta la atrapante historia de como Daniel Bernoulli (y no Johann, su padre) llego a derivar la ley que hoy -injusta y confusamente- solo lleva su apellido. Es sin duda una historia que mezcla la lucha de Daniel por triunfar como fisico-matemático, envidiando secretamente a Newton por sus avances en la mecánica y al mismo tiempo intercambiando correspondencia con Leibniz acerca del desarrollo del calculo diferencial; viendo morir a su hermano en Rusia y sufriendo la traicion de su padre.

Les dejo aquí el libro completo en formato PDF. El capitulo al que hago mención (aunque los recomiendo todos!) comienza en la pagina 43 del documento. Aunque sus contenidos no son imprescindibles para el curso, les recomiendo fuertemente su lectura.

Espero que les resulte útil.