En este post les dejo dos visualizaciones experimentales de la inestabilidad de Kelvin-Helmholtz que mencionamos en las clases teoricas.
Espero que les sea util.

En este post les dejo dos visualizaciones experimentales de la inestabilidad de Kelvin-Helmholtz que mencionamos en las clases teoricas.
Espero que les sea util.
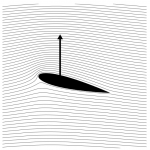
“La explicación más extendida del empuje es común, rápida, suena lógica y nos da la respuesta correcta, al tiempo que introduce conceptos erróneos, emplea un argumento físico sin sentido y evoca engañosamente la ecuación de Bernoulli”,
afirma Holger Babinsky (Cambridge Univ.) en su artículo “How do wings work?”, aparecido en 2003 en Physics Education. Los invito a leerlo para saber cómo un sencillo análisis de los gradientes de presión y de la curvatura de las líneas de corriente (como discutimos durante la última teórica) provee la explicación física más precisa y completa. Encontrarán el artículo siguiendo este link.
Espero que les sirva.
Anton Flettner fue el primero en concebir y construir una embarcación capaz de propulsarse explotando el resultado que obtuvimos hoy para la fuerza sobre un obstáculo cuyo contorno tiene una circulación atrapada y que enfrenta un flujo uniforme (fuerza o efecto Magnus).

La idea de Flettner fué construir una embarcación sin velas ni motores, en la cuál un cilindro vertical instalado sobre la cubierta se hiciese rotar a velocidad y dirección controladas de forma de obtener una fuerza sobre el navío en la dirección deseada. A dicho sistema se lo denominó rotor Flettner. Concretamente Flettner utilizó una embarcación preexistente (llamada Baden-Baden) la cuál hizo modificar y rebautizó como Buckau. Este sistema de propulsión demostró fehacientemente su potencialidad como medio de propulsión eólica para embarcaciones cuando el Buckau logró cruzar el océano Atlántico en 1926. Les dejo una foto del Buckau (ex Baden-Baden) junto a estas líneas.
Espero que les sea util (y divertido)!
Aqui el video:
Un montaje experimental comúnmente utilizado para producir y estudiar flujos potenciales bidimensionales es la celda de Hele-Shaw, introducida hace más de 100 años por Henry Hele-Shaw. Una celda de Hele-Shaw consiste esencialmente en el flujo de un líquido viscoso entre dos placas plano-paralelas ligeramente separadas entre sí.
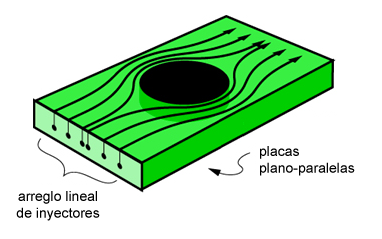
La figura muestra un esquema simple de una celda de Hele-Shaw, ilustrando el flujo en torno de un obstáculo; un arreglo lineal para la inyección de colorante (como trazador) y algunas líneas de corriente a modo de visualización. El flujo dentro de la celda, laminar y paralelo, se conoce como flujo de Poiseuille plano y será objeto de estudio en la segunda mitad de la materia (en el marco de la guía de flujos viscosos).
Una propiedad paradójica de la celda de Hele-Shaw es que, a pesar de que el flujo es viscoso, las líneas de corriente bidimensionales que se observan tienen las propiedades de un flujo potencial. No se alarmen: más adelante en el curso veremos en detalle cómo probar esta afirmación.
Les dejo además un video que muestra el dispositivo experimental de Hele-Shaw y su operación. El obstáculo empleado (un cilindro en este caso) es ubicado en el pequeño espacio entre dos placas de vidrio dispuestas verticalmente. Un fluido viscoso y transparente se carga en un reservorio sobre la celda y se lo deja fluir a través de ella bajo la acción de la gravedad. El dispositivo cuenta además (como es usual) con un arreglo lineal de inyectores equiespaciados por donde se hace ingresar un fluido coloreado de iguales características (viscosidad, densidad, etc.). El reservorio se mantiene continuamente alimentado con fluido transparente y la visualización comienza haciendo ingresar el trazador al sistema. Para incrementar el contraste de las líneas observadas, se suele emplear un trazador fluorescente y trabajar a oscuras iluminando únicamente el flujo en la celda. Pueden visualizar el video haciendo click sobre la imagen asociada.
Finalmente, les dejo dos videos más: dos visualizaciones experimentales de las líneas de corriente de un flujo potencial bidimensional uniforme que enfrenta (a) un obstáculo cilíndrico y (b) un perfil alar; ambas obtenidas con la celda de Hele-Shaw mostrada en el primer video.
Espero que les sea util.
Este caso es de interés por dos razones. Por un lado, el ejemplo sirve como ilustración del método general para el cálculo del potencial complejo de un flujo singular (i.e., que incluye singularidades). Por el otro, vemos que calculamos, como les comente en clase, el potencial complejo para los dos ‘ladrillos fundamentales’ de los que están constituidos todos los flujos que consideraremos en esta práctica: una fuente isótropa de caudal constante y un vórtice (dos casos límite que surgen de lo visto en clase y de lo expuesto en este documento).
Cualquier flujo que resulte combinación de ellos (p.ej., dipolos) podrá calcularse fácilmente a partir del resultado que vimos en clase (y que les describo en detalle en el documento que les adjunto) dado que las ecuaciones para la función potencial y la función corriente responden al principio de superposición.
Espero que les sirva.
En concreto, estaremos calculando la fuerza de anclaje necesaria para retener un stent en la aorta abdominal humana. Un ‘stent’ medico es un dispositivo tubular metalico en forma de malla usualmente flexible, que tiene el proposito de ensanchar y/o mantener abiertos pasajes naturales del cuerpo que han sido ocluidos por alguna condicion medica (ver figuras en el PDF debajo). La colocacion quirurgica de stents es una practica usual actualmente, por lo que existen stents arteriales, esofageos, biliares y ureterales, entre otros. La mayor parte de los stents son mantenidos en el lugar de colocacion por la presion de expansion que el mismo dispositivo ejerce contra la pared del pasaje donde es instalado. Sin embargo, en los ultimos años se han reportado casos de migracion de stents que debieron luego ser removidos quirurgicamente por presentar riesgos a la salud del paciente.
En este post les propongo calcular la fuerza que el flujo sanguineo ejerce sobre un stent ubicado en la aorta abdominal humana, a fin de explicar la migracion observada en pacientes y estimar la fuerza de anclaje necesaria para evitarla.
El enunciado completo de este problema adicional, asi como una resolucion sugerida, podran encontrarlo en esta notebook de Mathematica (para quien desee ejecutarla o editar el documento original) o bien en este documento PDF construido a partir de ella.
La idea es que, ademas de visitar los contenidos teóricos de la materia, vean como es posible plantear este tipo de problemas usando el motor de matematica simbolica de Mathematica.
Espero que les sea util.
Ya esta disponible el cronograma de la materia (en la pagina asociada). De acuerdo al mismo, el primer parcial de la materia tendrá lugar el día 15 de Octubre, y el segundo parcial el 3 de Diciembre.
En este post les dejo el link a la notebook de `Python` en Colaboratory que usamos en la teórica de hoy para analizar los efectos que cada término del tensor de deformación representa.
La notebook podrán encontrarla haciendo click aquí.
Espero que les sirva.
Como acceder a la notebook? Haciendo click en el link, y conectados a su cuenta de Google:
Las visualizaciones (videos, gráficos y animaciones) pueden tardar en cargar o generarse, sean pacientes!
Para quienes todavia no se hayan inscripto a la materia, les comento que el proceso de inscripcion consiste en que uds. me envien a mi un mail con los datos que les comento a continuacion. Yo paso la lista completa a la Secretaria Academica de la Facultad y son ellos quienes se encargan de hacer efectiva la inscripcion.
Les voy a pedir entonces, a todes les que se deseen inscribir a la materia (y no lo hayan hecho via el sistema SIU Guarani oportunamente) que me envien un e-mail con el subject “REINSCRIPCION E12020″ y los siguientes datos:
El deadline para esto es el proximo lunes 14 de septiembre. Mi mail es cobelli at df uba ar.