Hola, ayer en la clase vimos dos ejemplos de procesos que involucraban un pión y un nucleón. Para los piones les conté que forman un multiplete de I=1, son los más conocidos por ser los menos masivos.
En la guía aparecen otras partículas. A esta altura no tenemos un modelo que nos diga que isospin podrían tener, lo ponemos a mano viendo cuantas partículas se agrupan según su masa. Ya lo vamos a tener, en la guía 3 (el modelo de quarks).
Les cuento sus isospines por si quieren hacer esta guía:

• Deuterio (pn): este podríamos calcularlo en realidad. Al estar formado por p+n (es un isótopo del hidrógeno), usando la tabla de C-G vemos que hay dos opciones:1) |1,0> = (|p,n>+|n,p>)/√2
  2) |0,0> = (|p,n>-|n,p>)/√2Si le asignáramos la funcion de onda 1), entonces el deuterio pertenecería a un multiplete de I=1. Es decir que habría otras dos partículas dadas por |1,1>=|p,p>=He² y |1,-1>=|n,n> con masas similares.
  Como no se observan estados ligados de tales partículas, concluimos que |d>=|0,0>.

• Las partículas Σ y Σ* forman tripletes de Isospin, I=1. Recordemos que las ordenamos por su carga: a mayor carga, mayor I₃. Entonces |Σ⁺>=|1,1>, como en los piones. Los dos grupos se diferencian en su spin: las Σ tienen spin 1/2, mientras que las Σ* tienen spin 3/2. Más sobre eso en la guía 3.

• Los Kaones son complicados. En principio son 4: K⁺,K⁰,\bar{K}⁰,K^-. Así que uno diría que como (2*I+1)=4 entonces I=3/2, como sucede para las partículas Δ (Δ⁺⁺,Δ⁺,Δ⁰,Δ^-).Pero resulta que hay que separarlos en dos multipletes distintos de I=1/2. Uno formado por |K⁺>=|1/2,1/2> y |K⁰>=|1/2,-1/2>. El otro formado por |\bar{K}⁰>=|1/2,1/2> y |K^->=|1/2,-1/2>.Nuevamente diferiremos la explicación de esto hasta tener el modelo de quarks en la guia 3.

Respecto de los scatterings Pion-Nucleon que hablamos ayer, pueden encontrar más info en este capítulo del Libro Modern Physics (Second Edition) – For Scientists and Engineers de John Morrison: [Morrison] (John, no Jim!).

En las págs 306-310 cuenta como descubrir resonancias a través de masas invariantes, algo que mencioné muy por arriba hacia el final de la clase.

En la pág 325 habla de Pi-N scattering y muestra esta figura para las secciones eficaces:

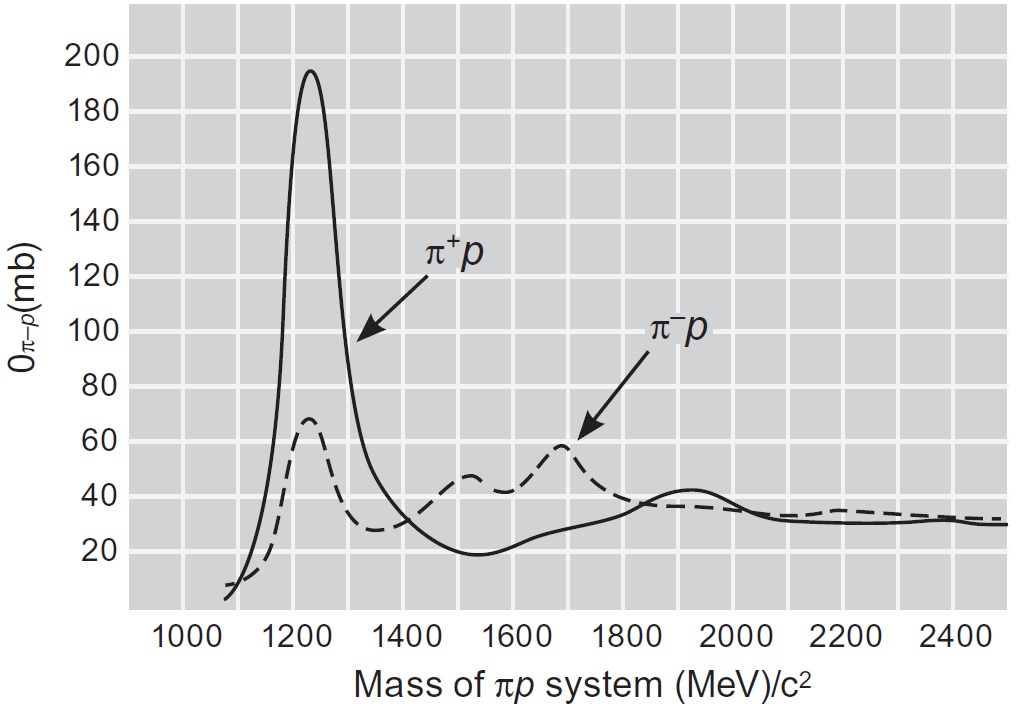Como se ve hay una resonancia alrededor de 1200 MeV: corresponde a la masa del Δ⁺⁺.
La figura original la puede encontrar en un artículo de 1957 (fig 3): [Lindenbaum].
En uno anterior con resultados preliminares pueden encontrar confusas discusiones respecto de la idea de resonancia y estados con isospin definido y su conservacion: [Anderson].

Se puede ver que el pico del scattering del π⁺ es 3 veces más grande que el del π ^-.
De hecho, pueden probar esto. Usando lo visto en clase, calculen el cociente entre secciones eficaces para los decaimientos totales [el π⁺ decae según el proceso a), pero el π ^- según los procesos b) y c)]. Muestren que:
σ_tot(π⁺+p)/σ_tot(π ^-+p) = σ_a/(σ_b+σ_c) → 3 , cuando domina el canal I=3/2.

Felicitaciones: ya tienen su primera predicción experimental!