En la página de la materia de años anteriores pueden encontrar varios ejercicios resueltos y ejemplos que prepararon docentes de Física Teórica 1 en el pasado. Ese material, junto con el material disponible en Material Adicional, puede ayudarlos a la hora de resolver los ejercicios de las guias.

Les dejo aquí un ejemplo de separación de variables en coordenadas esféricas que preparó Pablo Capuzzi en 2013:

Un problema de fácil resolución en coordenadas esféricas es el potencial electrostático generado por un casquete esférico de radio a cargado con densidad superficial uniforme σ con un agujero. Es decir, una esfera truncada o sin tapa. El agujero se puede caracterizar por el ángulo α de la coordenada azimutal de coordenadas esféricas. A modo de verificación del cálculo una vez hecho esto uno puede recuperar el resultado de la esfera completa.

El resultado completo en función de (r,θ) es el siguiente:

$\phi(r,\theta)=2\pi\sigma a \begin{cases} \left(1+\cos(\alpha/2)\right) + \sum\limits_{l=1}^{\infty} \dfrac{r^l}{a^l} \left[P_{l+1}[\cos(\alpha/2)] – P_{l-1}[\cos(\alpha/2)]\right] \dfrac{P_{l}(\cos\theta)}{2l+1} & \text{si } r<a \\ \left(1+\cos(\alpha/2)\right)\dfrac{a}{r} +\sum\limits_{l=1}^{\infty} \dfrac{a^{l+1}}{r^{l+1}} \left[P_{l+1}[\cos(\alpha/2)] – P_{l-1}[\cos(\alpha/2)]\right] \dfrac{P_l(\cos\theta)}{2l+1} & \text{si } r > a \end{cases}$

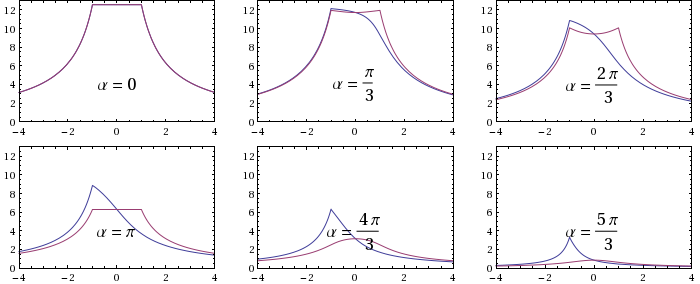
En la figura se ven, para 6 valores de α, el potencial electrostático a lo largo del eje z (en azul) y a lo largo de un eje perpendicular a z (en rojo).

Para el que tenga ganas de explorar la solución del potencial para distintos parámetros, pueden bajar de acá una notebook de ipython con la expresión correspondiente y algunos gráficos, o ver directamente el resultado acá.