En un post de la última semana se habló de radiación cósmica de fondo, curvatura del espacio y agujeros negros. Quedó implícita la mención de que Maxwell también se impone en la relatividad general, obteniendo así las ecuaciones de Einstein-Maxwell. A fines de la década de 1960 se derivó, a partir de estas ecuaciones, que la solución de un agujero negro está completamente caracterizado por 3 observables: su masa, su momento angular y su carga eléctrica. Esto significa que toda otra información acerca de cómo se formó y lo que atravesó el horizonte de eventos queda clásicamente inaccesible para un observador externo. Se dice que un agujero negro no tiene pelos (aunque puede tener los 3 pelos de Homero en la imagen), porque no tiene ningún otro momento multipolar asociado. A este resultado se lo conoce como no-hair theorem, y junto con la radiación (cuántica) de Hawking, dan lugar a la paradoja de la pérdida de información.

En 1971, estando al tanto del teorema de agujeros negros sin pelos, Cohen y Wald plantearon el problema electrostático de una carga de prueba frente a un agujero negro de Schwarzschild de masa m (sin carga eléctrica, ni rotación). Ubicaron una carga q en el eje z para tener simetría azimutal y, tras unos pocos pasos intermedios, llegaron a la siguiente ecuación para el potencial electrostático en el espacio curvado por el agujero negro

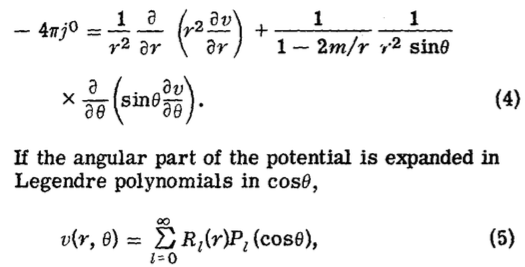
Ecuación de Poisson en la geometría de Schwarzschild, donde J^0 representa la densidad de carga eléctrica de una carga puntual.

Notarán la similitud entre esta ecuación y la que plantearon en la clase teórica de la materia, usando coordenadas esféricas en el espacio plano. Cohen y Wald usaron separación de variables y expresaron el potencial con un desarrollo en Polinomios de Legendre, exactamente igual a lo que haríamos nosotrxs. La diferencia está en las soluciones radiales, hay un horizonte de eventos que complica un poco la solución, pero no mucho. Dejando de lado detalles, destacamos 2 cosas del  resultado de su artículo:

• El horizonte de eventos es una superficie equipotencial.
• Usaron la solución estática para estudiar qué pasa al acercar la carga lentamente hacia el agujero negro de Schwarzschild.

Sucesión de configuraciones estáticas (sin dinámica) de una carga de prueba q frente a un agujero negro de Schwarzschild. Al ubicar q sobre el horizonte sólo queda la carga total y desaparecen todos los otros momentos multipolares.

Las similitudes con un conductor esférico son asombrosas. Para completar la historia vale la pena mencionar que unos pocos años después se encontró que la expansión multipolar del potencial de una carga q frente a Schwarzschild se podía re-sumar en forma cerrada, el resultado fue presentado por B. Linet y es llamativamente simple:

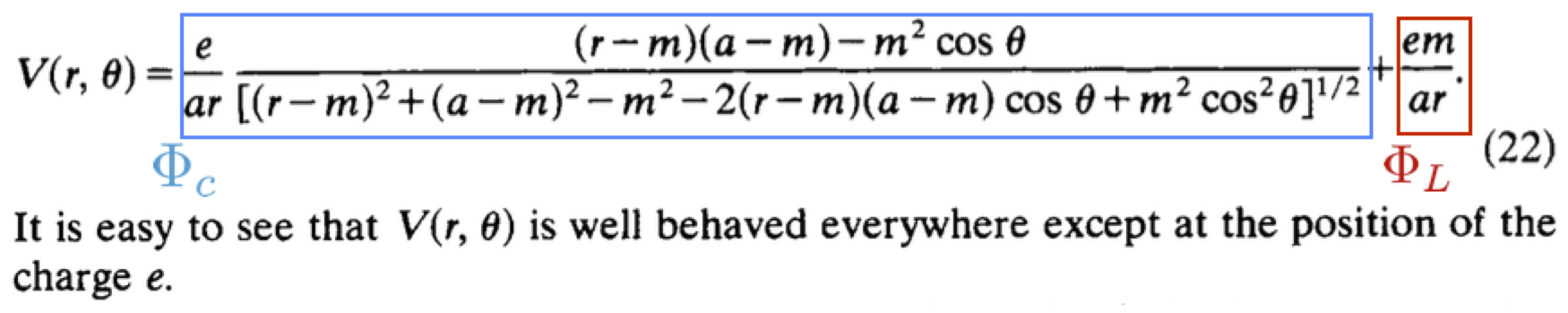
Potencial para una carga "e" en Schwarzschild. Notar que al evaluar en m=0 se obtiene el potencial de una carga en el espacio Euclídeo vacío, idéntico a la ec.(88) del apunte FT1_práctica10

El primer término de arriba (azul en la figura) se obtuvo como una solución local de la carga en la geometría de Schwarzschild y se conoce como potencial de Copson, por el matemático que la publicó el en el año 1928. Copson olvidó imponer una condición de contorno asintótica, por lo que el resultado global era físicamente insatisfactorio y no se le dio mucha importancia. Casi 50 años después, Linet comprendió que la solución cerrada de Copson era correcta si sumaba el término φ_L (rojo en la figura), y mostró que el desarrollo de Cohen y Wald coincide con el potencial de Copson + Linet.

El  potencial φ_L que faltaba sumar en el año 1928 es un término monopolar necesario para quitar el exceso de carga a la solución de Copson y que el resultado refleje que Schwarzschild es un objeto sin carga eléctrica neta. Para eso lo que se usó fue el teorema de Gauss y así se garantizó que la carga total del problema fuera sólo q, la de la carga de prueba. La construcción que hizo Linet es completamente análoga a la que hacemos en los problemas externos a conductores esféricos cuando agregamos un término monopolar (“una carga en el centro”) para conseguir que quede un conductor descargado y que su superficie siga siendo equipotencial (recuerden los ítems (e) de los problemas 21 y 22,  FT1_práctica10).

Sucesión de configuraciones estáticas (sin dinámica): Equipotenciales de una carga de prueba frente a un agujero negro y frente a un conductor perfecto.

Mas allá de que faltaba un término monopolar, observen que φ_C  es -por sí solo- equipotencial sobre la superficie del horizonte de eventos (en unidades geométricas, esto es evaluar en r=2m, el horizonte). Además, en su artículo de 1928, Copson mencionó que “el potencial es independiente de la posición donde se ubique el electrón sobre la esfera del horizonte“, lo cual él calificó sencillamente como “a rather curious result“. Lo curioso del problema electrostático de la carga de prueba en la geometría de Schwarzschild es que predijo algo certero acerca de la calvicie eléctrica de los agujeros negros 40 años antes de que se formulara el teorema de agujeros negros sin pelos.