Hoy consultaron los ejercicios de la parte IV. Sistemas Compuestos de la guía 3 de postulados. Subimos aquí un breve comentario sobre su resolución, con cuentas → 0.
Author Archives: Mateo Koifman
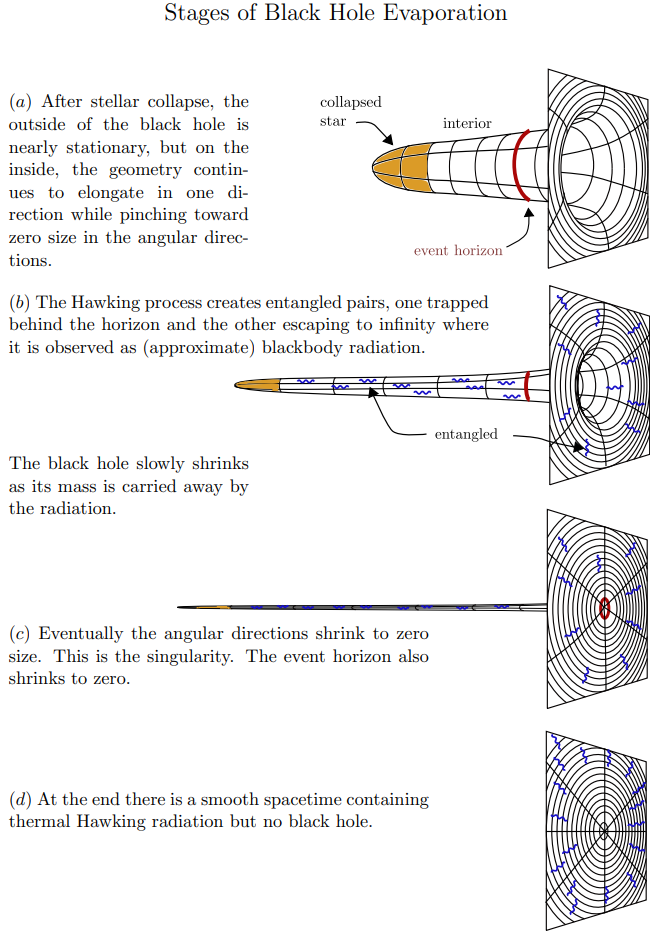
Entrelazamiento, información y agujeros negros: La “paradoja” de Hawking
La primera solución de las ecuaciones de la relatividad general de Einstein se publicó en 1916. Casi 5 décadas le llevó a la gente darse cuenta que esa solución era un agujero negro y que muchas estrellas podrían terminar sus días como uno de ellos. En los ’70s, Cygnus X-1 se volvió comúnmente aceptado como el primer agujero negro hallado en el cielo (y ya no sólo en la hoja). Esto motivó un montón de preguntas. En particular: cómo se llevan los agujeros negros con la segunda ley. Los descubrimientos de Bekenstein y Hawking fueron notables: Los agujeros negros cumplen las mismas leyes de termodinámica de física 4, con su propia entropía y temperatura. Los resultados de 1974 de Hawking dicen que un agujero irradia (fotones, principalmente), con una distribución de probabilidad térmica (esto es análogo a la radiación de cuerpo negro de F4, donde hay una distribución de probabilidad de frecuencias emitidas) y que si esperamos un poco* (típicamente entre 10^67 y 10^94 años, más o menos lo que le lleva a Racing salir campeón del Apertura) los agujeros negros se evaporan completamente. Hasta acá, nadie pone muy en duda ninguno de estos resultados. Lo que sigue no estamos tan seguros.
Hawking planteó entonces el siguiente escenario: Cada fotón emitido (y la configuración completa del campo con todos los fotones) necesariamente es un estado mezcla, porque sólo conocemos una distribución de probabilidad para la radiación. Uno entonces puede tener inicialmente una estrella en un estado global puro ψ, que colapsa y un -largo- tiempo después se evapora completamente, de forma tal que su estado final es un estado global mixto ρ. Esto está absolutamente prohibido para cualquier sistema cuántico ordinario cerrado que evoluciona unitariamente: Un estado puro global nunca puede evolucionar unitariamente a uno mixto global (Si tengo un ket, la ecuación de Schrödinger me da otro ket! O bien, la pureza de la matriz densidad no cambia cuando evoluciona con el U(t) que vieron hoy en la teórica). Claro, no sabemos describir los sistemas que gravitan como sistemas cuánticos ordinarios. Ni siquiera estamos seguros de que lo sean. Sin embargo, este escenario provocaría -como titula Hawking en su paper- una ruptura de la predictibilidad de la física. Uno un poquito se incomoda cuando lee esto… es como si a veces no existiera una ecuación de Newton para predecir x(t). (Tengamos en cuenta que acá no es que estamos haciendo ninguna medición cuyo resultado sea azaroso. La mecánica cuántica siempre nos permite predecir el estado del todo con 100% de certeza en un sistema cerrado como lo es el universo).
Y entonces? Bueno, quizás tenemos que tragarnos que en la naturaleza la información se pierda y nunca seamos capaces de predecir el futuro. No lo sabemos. Pero si no, habrá alguna forma de que el agujero negro emita fotones con una distribución térmica, se evapore y así todo al final el estado vuelva a ser puro? En realidad no hay nada sorprendente en que el estado de la radiación sea mixto -al menos al principio- por motivos que vimos en la materia: Que el estado del universo sea puro, no quiere decir que el estado de las partes vaya a ser puro. Y efectivamente este es el caso: Si el interior y exterior del agujero negro forman un sistema compuesto, y “tomamos la traza parcial sobre el Hilbert que describe el interior” (si eso acaso tiene sentido), nos vamos a encontrar con un estado entrelazado. Heurísticamente, se suele decir que la evaporación de Hawking se debe a la creación de pares de partículas: una escapa al infinito, su pareja cae al agujero. Si imaginamos a estas partículas como pares de spin, no es sorprendente que las que logran escapar estén entrelazadas con las que caen. Siguiendo esta línea, en 1993 Page propuso (el de Zeppelin no, Don Page) que si la evolución fuera unitaria, más o menos a la mitad de la evaporación la aproximación de Hawking ya no vale y el estado ρ debería empezar a purificarse. Esto es porque la entropía de entrelazamiento la matriz densidad reducida (que se calcula como Tr[-ρ log(ρ)]) no puede ser más grande que la entropía termodinámica del agujero negro, proporcional a su área que está disminuyendo. En un lenguaje más rústico, cuando el agujero negro es más pequeño ya no hay tantos grados de libertad disponibles para entrelazar con el exterior.
Recientemente (en 2019) se encontró una fórmula para la entropía, muy similar a la fórmula original de Ryu y Takayanagi (anunciados el mes pasado ganadores de la medalla Dirac que hoy les contaba, junto a Casini y Huerta del Balseiro) y que reproduciría la curva para la entropía que propuso Page. Según Maldacena parecería que el problema de calcular la entropía consistente con unitariedad (osea, estado final puro y sin que se pierda información) estaría resuelto, pero quedaría otra parte importante sin resolver: Cómo se calcularía ese estado puro final?
Como reflexión final: este es un escenario que nos invita a pensar qué ocurre cuando juntamos la gravedad y la cuántica (van a encontrar un ħ en las fórmulas de la entropía y temperatura, dando cuenta que este es un efecto de gravedad semiclásica. No es gravedad cuántica propiamente). Por otro lado, es sólo uno de los problemas en los que la teoría de la información ha sido de gran ayuda en la física teórica de altas energías en los años recientes. Para quienes quieren indagar un poco más, les comparto un link a una de las clases de Termodinámica Avanzada del 2020 donde pueden encontrar una introducción más detallada y, al final, esta misma paradoja https://youtu.be/lTW_FxdeS-Q?&t=5646.
*En realidad, eso sólo sería cierto en vacío. Sin embargo sabemos que el universo está a una temperatura de 2.7K.
Una aparente paradoja en el formalismo
Pueden encontrar una respuesta muy breve en Mathematical surprises and Dirac’s formalism in quantum mechanics (de aquí tomamos la “paradoja”, es el ejemplo 3). Para hacer física cuántica, probablemente nos alcance con la intuición que tenemos de espacios vectoriales de dimensión finita; este es el nivel de detalle que vimos y suele tratarse en los libros. Pero si de saciar curiosidades se trata, el artículo concluye que “Las aparentes contradicciones pueden ser reformuladas de la siguiente forma: La teoría de operadores lineales en espacios vectoriales de dimensión infinita es más complicada e interesante que la teoría de matrices de orden finito”. El texto es bastante pedagógico y son todos ejemplos de la mecánica cuántica.
Y recuerden: El espectro de operadores auto-adjuntos es siempre real.