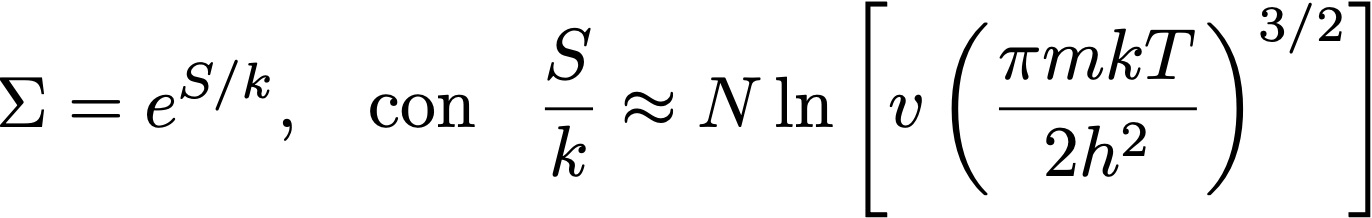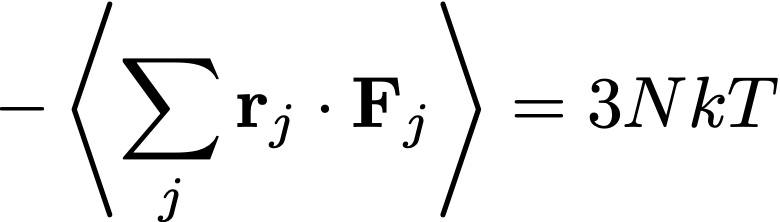En la película Spectral (disponible en Netflix), unos condensados de Bose-Einstein toman vida y congelan a las personas hasta la muerte. Por suerte, gracias al poder de la ciencia, pueden ser atrapados por materiales cerámicos y por el hierro, y por una pistola de pulsos que destruye al condensado (Yeah, science!). En el laboratorio hay pocas chances de que un condensado de Bose-Einstein cobre vida (pero por las dudas, no se acerquen al Laboratorio de Iones y Átomos Fríos del DF). Así que en este post vamos a ver cómo se ve un condensado en la realidad.

A continuación les dejo algunos videos sobre condensados de Bose-Einstein. Como los videos son largos, para aquellos que tienen síndrome de déficit de atención les digo también a qué instante pueden saltear para ver algunas cosas interesantes. Como mencioné en la última clase, recién en 1995 se realizaron los primeros experimentos de condensados de Bose-Einstein en gases diluídos de átomos ultrafríos, en los que la interacción entre los átomos es débil:

El video muestra un experimento con un gas de átomos de sodio. La descripción del experimento ocurre entre el minuto 0:46 hasta 2:50. A partir del minuto 3:10 hasta 3:50 pueden ver mediciones de la temperatura en el gas, y la formación del condensado de Bose-Einstein.

Los que tengan un poco mas de paciencia pueden ver la charla completa de Eric Cornell cuando recibió, junto con Carl Wieman y Wolfgang Ketterle, el premio Nobel por conseguir el primer condensado de Bose-Einstein gaseoso en el laboratorio:

Nobel Lecture by Eric A. Cornell

El video dura 39 minutos. Los que quieran pueden saltear la introducción e ir al minuto 5:23 hasta 7:03, donde Cornell explica el rol que juega la longitud de onda de de Broglie en la transición de fase (algo que vimos en las últimas clases). A partir del minuto 28:49, Cornell muestra imagenes de vórtices cuantizados en el condensado, un tema que veremos en la próxima clase. En el próximo post, videos de superfluidos escapándose espontáneamente de sus recipientes (¡seguro hay una película de ciencia ficción que usa este fenómeno!).

El video de la última cláse teórica, y los apuntes para la próxima clase, están disponibles acá. Y no se olviden de llenar la encuesta obligatoria, siguiendo las instrucciones en este post. ¡Si no la llenan, despídanse de la materia!

¡Les recuerdo que este lunes es feriado, así que la próxima clase es el miercoles!

Todos los cuerpos absorben radiación electromagnética, y emiten espontáneamente una parte en forma de radiación en equilibrio térmico con el cuerpo (es decir, como fotones a la misma temperatura que la fuente térmica). Esa es la radiación de cuerpo negro. Arnold Schwarzenegger sabe mucho sobre esto, y se cubre en barro frío cada vez que tiene que luchar contra un depredador, porque estos aliens pueden ver la radiación emitida por su cuerpo. Pero todos emitimos esta radiación, no solo Arnold (la radiación no depende de cuantas horas pasemos en el gimnasio). Así que en este post vamos a ver cómo esto se puede usar para saber qué temperatura tienen las personas en los aeropuertos.

¿En qué longitud de onda emite radiación de cuerpo negro una persona a 36 grados Celsius? A partir del espectro de Planck se puede ver que la máxima emisión ocurre para una longitud de onda que sigue la ley de Wien,

donde b = 2898 μm K. Noten que esto significa que al cambiar la temperatura del cuerpo, cambia el “color” de la radiación electromagnética emitida, ya que el color depende del espectro emitido (y fuertemente de en qué longitud de onda está el pico del espectro). Entonces ¿en qué longitud de onda debe observar una cámara para detectar este tipo de radiación? Para 36 grados Celsius, T= 309 K, y λ_max ≈ 9.4 μm. De hecho, si variamos la temperatura entre 30 y 40 grados Celsius, el máximo del espectro varía respectivamente entre 9.56 y 9.26 μm (o entre 9560 y 9260 nm). Esto corresponde a radiación electromagnética infraroja. ¡Así que mirando los colores en una cámara infrarroja podemos estimar la temperatura de los cuerpos! Y así también sabemos en qué región del espectro electromagnético funcionan los ojos del depredador que persigue a Schwarzenegger.

Sabiendo esto, ¿a qué temperatura se encuentra la radiación cósmica de fondo? Como vimos en clase, estamos rodeados por radiación electromagnética de cuerpo negro que fue emitida en el momento en que se formaron los primeros átomos en el universo. En 1964, Arno Penzias y Robert Wilson, realizando mediciones con una antena en los Laboratorios Bell, encontraron una extraña señal de microondas con un máximo en λ_max ≈ 1 mm. Usando la ley de Wien, esta longitud de onda corresponde a T ≈ 2.7 K (la temperatura determinada originalmente por Penzias y Wilson en 1964 era ligeramente mayor, por la incerteza experimental del instrumento).

Como siempre, en la página de la teórica encontrarán el último video de las clases, y material para la próxima clase. Y no dejen de mirar el siguiente post de Guillem, sobre una noticia reciente de condensados de Bose-Einstein, el tema de la próxima clase.

No es el nombre de una banda de rock (¡podría serlo!). Es la historia de Subrahmanyan Chandrasekhar y un tipo muy particular de estrellas. Chandrasekhar ganó el premio Nobel en 1983 por sus estudios sobre la evolución y la estructura de las estrellas, pero su camino hasta ese premio no fue fácil. El Dr. Chandra, un personaje en 2001: A Space Odissey, lleva su nombre en homenaje a él.

En las últimas clases comenté que la presión de degeneración en un gas de fermiones es central para explicar la estabilidad de estrellas enanas blancas (y también juega un rol en estrellas de neutrones). Una enana blanca es una estrella que quemó todo su material nuclear: una estrella como el Sol, luego de quemar todo el hidrógeno, quema material nuclear más pesado como el Helio. Para ello necesita mayor presión y temperatura en el núcleo, pero también genera mas energía en la reacción nuclear, y se expande hasta convertirse en una gigante roja. Luego de quemar todo el material disponible para la fusión, sufre una inestabilidad y expulsa buena parte de su masa. El núcleo de la estrella, que puede tener una masa equivalente a la del Sol pero comprimirse hasta un volumen como el de la Tierra, mantiene el calor residual y forma la enana blanca. La siguiente imágen muestra a Sirius B, una enana blanca, indicada por la flecha:

Si una enana blanca no quema más material nuclear, ¿qué mantiene a la estrella estable evitando el colapso gravitatorio? La respuesta es la presión de degeneración en un gas de Fermi: en la estrella la densidad de la materia es tan grande que el gas está degenerado, y y la presión de Fermi es suficiente para contrarrestar la fuerza de gravedad. Algo parecido ocurre en estrellas inicialmente aún mas masivas, que pueden evolucionar a estrellas de neutrones. Finalmente, si la masa inicial de la estrella es aún mayor (más grande que la masa límite de Chandrasekhar), la presión de degeneración no es suficiente para evitar el colapso gravitatorio y se puede formar un agujero negro.

Los que quieran leer mas detalles sobre el balance de fuerzas en una estrella enana blanca pueden ver el siguiente link (9 páginas, en inglés):

Propiedades de enanas blancas y el gas degenerado de electrones

Las contribuciones de Chandrasekhar al estudio de interiores estelares, la evolución de las estrellas hasta la formación de enanas blancas o agujeros negros, y sus estudios de la estadística de Fermi-Dirac para explicar la estabilidad de las enanas blancas, lo llevaron a tener diversas disputas con astrónomos renombrados de la época, como Arthur Eddington. Los que quieran conocer parte de esta historia, más detalles sobre evolución estelar y la formación de agujeros negros, y algunos detalles jugosos sobre la pelea entre Chandrasekhar y Eddington, pueden ver este video:

Finalmente, en la página de la teórica van a encontrar el video de la última clase, los apuntes corregidos de la clase anterior, y el apunte de la próxima clase.

Después de una pausa en los posts para que Anubis pudiera pesar sus corazones en una balanza contra una pluma de Maat (es decir, para que fueran evaluados), retomamos las discusiones sobre temas relacionados con la materia. Un detalle menor que nos olvidamos de mencionar es que si fallan en esta evaluación, y su evaluación pesa más que una pluma de la diosa de la verdad y la justicia universal, Ammyt devorará sus corazones. La resolución correcta de los ejercicios la pueden ver en el post anterior. Aclarado esto les recuerdo que, como siempre, en la página de la teórica ya están disponibles el video de la última clase, y los apuntes para la próxima clase. Y ahora sí, el gato de Schödinger, estadística cuántica y Philip J. Fry:

El título del post hace referencia al entrelazamiento cuántico o “spooky action at a distance“, mientras que el video muestra a Erwing Schrödinger violando la ley en Futurama. En las últimas clases vimos cómo contar microestados en el caso cuántico. No es lo mismo considerar un gas de fermiones o de bosones, por la simetría que debe cumplir la función de onda frente al intercambio de partículas. Pero además, a la hora de contar configuraciones microscópicas posibles, tampoco es lo mismo tener partículas independientes o tenerlas en un estado entrelazado.

El siguiente paper, que fue publicado este año en Physical Review Letters (el link abajo lleva al preprint en arXiv), tiene una aplicación original e interesante del conteo de microestados en el caso cuántico (o de “spooky action” a muy corta distancia):

EPR paradox and quantum entanglement at subnucleonic scales

A energías suficientemente bajas, un protón está formado por tres quarks, cada uno con una carga de color (azul, rojo o verde) que deben sumar “blanco” para obtener la carga de color correcta del protón. Estos quarks están unidos dentro del protón por gluones. La pregunta que se hacen los autores del trabajo es sencilla: los partones (quarks y gluones) dentro del protón, ¿están en estados independientes, o están entrelazados? Esta pregunta puede parecer muy difícil de responder, pero llamativamente la mecánica estadística nos permite predecir cosas muy concretas que se pueden medir “macroscópicamente” de acuerdo al estado en el que se encuentre el sistema.

Como vimos al comenzar la segunda mitad de la materia, el conteo de estados cuánticos es diferente si el sistema está en un estado puro o si está en un estado mezcla. Si está en un estado puro (en este caso, en una única configuración posible correspondiente a un estado singlete), la entropía del sistema es cero (¡porque hay un único microestado!). Recuerden que en el ensamble microcanónico,

S = – k ln Γ

donde Γ es el número de microestados. Por otro lado, si la función de onda corresponde a un estado entrelazado, el conteo de estados posibles cambia (porque las combinaciones de estados que pueden armarse son diferentes), cambiando como resultado también el valor de la entropía.

Los autores usan esto para estimar el número de microestados compatibles con los vínculos dentro del protón en cada caso, y vincular este número con la probabilidad de que se produzcan N partículas al final de ciertas colisiones que se pueden medir en el LHC. Así, una estimación estadística de la entropía del sistema les permite en principio distinguir en experimentos entre estados entrelazados y no entrelazados dentro del protón. Dejando de lado algunos detalles técnicos, los conceptos generales del paper se pueden entender al nivel de la materia.

Hace unos años, un grupo de científicos demostró que obtener ciertas propiedades macroscópicas a partir del conocimiento completo y preciso de las leyes microscópicas del sistema es indecidible. El problema particular que consideraron es el de calcular la diferencia de energía entre niveles de un semiconductor (el “gap espectral“, o la energía necesaria para mover un electrón del estado fundamental al estado excitado, en un sistema con muchos electrones). El valor del gap espectral tiene un impacto en el comportamiento macroscópico del sistema: los semiconductores tienen un gap espectral y sus propiedades físicas dependen de este gap, mientras que si no existe un gap, el material sufre una transición a otro estado.

Lo que se demostró es que conociendo completamente la física microscópica del sistema cuántico, la pregunta “¿tiene el sistema un gap espectral?” es indecidible. Que este problema sea indecidible significa que es imposible construir un algoritmo general que siempre nos de la respuesta correcta. Esto no significa que la pregunta no pueda contestarse, o que no pueda calcularse el valor del gap. Lo que significa es que el cálculo de esta propiedad macroscópica (aún conociendo completamente la física miscroscópica del sistema) no puede hacerse usando un único algoritmo que valga en todos los casos. En otras palabras, puede existir un algoritmo que permita obtener la respuesta para un material particular, pero que para otro material el mismo método no sirva. O, como dicen los autores del trabajo, “no puede existir un método general que permita determinar si un material descripto por la mecánica cuántica tiene un gap espectral o no”.

La demostración de indecibilidad se realizó mostrando que el problema es equivalente al problema de la parada de Turing. En 1936, Turing demostró que no es posible escribir un “programa” que ejecutado en una “computadora” (técnicamente, un algoritmo en una máquina de Turing) pueda decidir si otro algoritmo terminará de ejecutarse en un número finito de pasos o no. El teorema de Turing está relacionado con otros dos teoremas famosos de Gödel, que dicen (en su forma débil) que es imposible escribir en forma algorítmica un conjunto de reglas (o axiomas) para generar la aritmética que sea a la vez correcta y completa. Noten que si el sistema es incompleto, en algún momento encontraremos algún teorema válido que no podremos probar con los axiomas que tenemos. ¡Y si es incorrecto, en algún momento podremos probar que vale cierto teorema, y también que no vale ese mismo teorema!

Mas allá de los detalles técnicos, el resultado puede ser muy perturbador para los que esperaban que el curso de mecánica estadística les permita justificar, en forma sistemática, todo lo que no comprendemos de la física macroscópica a partir de fenómenos microscópicos (¡que probablemente tampoco comprendamos muy bien!). Para los que quieran saber más, pueden leer un artículo en Phys.org, o el paper publicado en la revista Nature:

• Quantum physics problem proved unsolvable (Phys.org)
• Undecidability of the spectral gap (paper)

Sin embargo, noten que este resultado no implica que no podamos obtener teorías físicas fundamentales, que no se pueda conocer el Hamiltoniano que describe la física básica del problema, o que no se pueda conocer si el sistema tiene un gap o no. Lo que implica es que no alcanza con saber matemáticas y usarlas como en una “receta”, y que siempre tendremos que hacer aproximaciones o consideraciones según la física de cada sistema.

En cierto sentido, esto tiene una relación con la visión de las jerarquías en la física de Feynman de un post anterior, donde Feynman decía que es un error pensar que uno puede partir de uno de los extremos (la física microscópica) y caminar solamente desde ese extremo hacia el otro (la física macroscópica), creyendo que de esa forma se alcanzará un entendimiento completo. En esta linea de pensamiento les aconsejo fuertemente leer también este genial artículo de 1972 de Philip Anderson:

• More is different

donde el señor Anderson entre otras cosas dice:

“The ability to reduce everything to simple fundamental laws does not imply the ability to start from those laws and reconstruct the universe [...] At each stage entirely new laws, concepts, and generalizations are necessary, requiring inspiration and creativity to just as great a degree as in the previous one.“

Este artículo de Anderson a veces es mal interpretado. Anderson no dice que los sistemas extensos sigan nuevas leyes fundamentales, o que nuevas fuerzas fundamentales aparezcan como resultado de considerar sistemas con nuevas partículas. Pero sí dice que conocer las leyes fundamentales no es suficiente para con ellas reconstruir el universo en forma sistemática, y que al considerar cada aumento en la escala del sistema, es necesario realizar nueva investigación en física básica, e introducir nuevos conceptos, nuevas ideas y nuevas generalizaciones.

¿Y por qué el Señor Anderson insiste con esto? ¿Por qué lo hace? Porque elige hacerlo:

Como siempre, en la página de la teórica van a encontrar el último video y los apuntes para la próxima clase.

¡Fin de semana largo a pura acción! En las últimas clases vimos como el límite macroscópico de la ecuación de Boltzmann nos da las ecuaciones de los fluidos para un gas muy diluido, y cómo el retorno al equilibrio del sistema puede caracterizarse, macroscópicamente, con coeficientes de transporte (¿qué equilibrio estaría intentando restablecer Frank Martin en sus tres películas?).

La validez del límite hidrodinámico puede verse también en simulaciones numéricas, y a veces la ecuación de Boltzmann o ecuaciones de dinámica molecular para un número muy grande de partículas se usan para simular la dinámica macroscópica de gases y líquidos. En clase vimos un ejemplo con apenas 400 partículas, pero con tiempo y paciencia pueden hacerse cosas más grandes. Tomemos el caso de una instabilidad macroscópica que ocurre en gases y líquidos cuando existe un gradiente tangencial en el momento del fluido: la intestabilidad de Kelvin-Helmholtz.

La inestabilidad de Kelvin-Helmholtz ocurre cuando dos fluidos (usualmente con densidad diferente) se mueven en dirección contraria. En la superficie que separa los dos fluidos el gradiente de velocidad es muy grande. Esta superficie es inestable frente a pequeñas perturbaciones, y al intestabilizarse se genera un patrón de vórtices conocidos como vórtices de Kármán. La intestabilidad que se desarrolla intenta recobrar una distribución homogénea del momento, y resulta en un mezclado y transporte eficiente entre las dos regiones del fluido. Pueden ver un ejemplo de macroscópico en la siguiente foto de unas nubes, noten “las crestas” en el borde superior de las nubes, que resultan en el transporte y mezclado del gas en la parte mas baja con el gas en la parte superior.

Esta misma inestabilidad puede verse en una simulación de dinámica molecular de la mezcla de dos gases usando 9.000.000.000 de partículas (¡comparen este número con las 400 que usamos la clase pasada!). Observen cómo se forman las mismas estructuras que en la foto, cómo la mezcla se vuelve cada vez más homogenea como resultado de las colisiones y el transporte, y cómo un flujo macroscópico emerge de la dinámica molecular microscópica:

Los que quieran aprender más sobre coeficientes de transporte, y sobre termodinámica de sistemas fuera del equilibrio, pueden leer sobre las relaciones recíprocas de Onsager, que permiten formalizar desde un punto de vista termodinámico algunas de las relaciones para los coeficientes de transporte que vimos en la última clase.

Finalmente, recuerden que el lunes 25 de mayo es feriado, así que no tendremos clase. Pueden aprovechar para ponerse al día con la materia, mirando los videos de las últimas clases, o mirando el apunte de la próxima clase, en la página de la teórica.

Hay armaduras de acero (tengan en cuenta que “Full Metal Jacket” se refiere a un tipo de munición, y no a un chaleco), alquimistas de acero, y se puede hacer termodinámica con bolas de acero. En la última clase definimos el tensor de presión a partir del tensor de flujo de momento en las fluctuaciones térmicas. El siguiente video ilustra como se relaciona la presión con el momento entregado por los choques de partículas contra las paredes de un recipiente. Y lo hace en forma muy visual, usando bolas de acero (bastante grandes) que se sacuden al azar dentro de un tubo:

Los que no hayan visto Full Metal Jacket, ya tienen mi recomendación de películas para el fin de semana. Pueden aprovechar y hacer una maratón de Stanley Kubrick. Para los que prefieran otro tipo de entretenimiento, el animé de Fullmetal Alchemist está en Netflix en sus dos versiones. Y no dejen de ver:

• El importante anuncio sobre la entrega de ejercicios prácticos en el post previo.
• El video de la última clase, y los apuntes para la proxima clase, en la página de la teórica.

“Ha llegado el momento de anunciar: Esta isla, con sus edificios, es nuestro paraíso privado. He tomado algunas precauciones -físicas, morales- para su defensa: creo que lo protegerán. Aquí estaremos eternamente -aunque mañana nos vayamos- repitiendo consecutivamente los momentos de la semana y sin poder salir nunca de la conciencia que tuvimos en cada uno de ellos.“

Adolfo Bioy Casares, La invención de Morel (1940).

La repetición eterna, como los espejos y la cópula para un heresiarca de Uqbar, es abominable (excepto tal vez para Friedrich Nietzsche). Probablemente nos parezca antinatural justamente porque nunca observamos en la naturaleza que las configuraciones de sistemas extensos se repitan exactamente de la misma forma. Esta observación fue una de críticas que Poincaré y Zermelo, entre otros, realizaron a la teoría estadística de Boltzmann. Imagino que Sísifo también tendría sus objeciones. Y a Dormammu tampoco le deben gustar las repeticiones:

En el teorema H de Boltzmann, su entropía casi siempre crece. Imaginemos un gas que ocupa la mitad de un recinto, separado en dos por un tabique. En un dado instante el tabique se retira, y el gas se expande hasta ocupar todo el recinto (con el consecuente aumento de la entropía). Dado que todas las configuraciones son equiprobables, en algún instante todas las moleculas del gas podrían estar en la primer mitad del recinto (al fin y al cabo, podemos tener configuraciones que incluyan a un cerebro de Boltzmann, ¿no?). Pero si en ese preciso instante volvemos a poner el tabique, recuperamos en forma espontánea la primera configuración, que tenía menor entropía. Este posible retorno a una configuración previa fue visto por Poincaré como un problema abominable para la teoría de Boltzmann (aunque más tarde Poincaré se convenció de su valor).

Efectivamente, si el número de configuraciones de un gas es discreto, existe una probabilidad no nula de que vuelva espontáneamente a una configuración previa (y si las configuraciones son contínuas, de que vuelva a una configuración arbitrariamente cercana a la configuración inicial). Pero el tiempo necesario para volver a encontrar esta configuración es increíblemente largo, lo que vuelve a este escenario irrelevante a fines prácticos. Estimemos esto para un metro cúbico de aire a temperatura ambiente (T = 300 K). Vimos que el número de configuraciones Σ de un gas ideal lo podemos calcular (en el ensamble microcanónico) como

donde S es la entropía, N el número de partículas, v el volúmen específico del gas, m la masa de las partículas (moléculas de N₂), k la constante de Boltzmann, y h la constante de Planck (ignoro un factor aditivo despreciable en la entropía). Usando valores típicos para estos parámetros (y considerando que v ≈ 5×10^-29 m³), obtenemos que el número de microestados o configuraciones posibles es

¡Este es un número enorme, con más de 10²⁵ dígitos! Asumamos ahora que las configuraciones cambian cada vez que hay un choque entre partículas. Es decir, cuando las partículas en el gas chocan, intercambian momento, y pasan de una configuración a otra. Para el aire a temperatura y presión ambiente, el tiempo entre choques es τ ≈ 10^-10 s. Y si todas las configuraciones son equiprobables, podemos estimar el tiempo medio para repetir una configuración como proporcional a Σ·τ, que sigue siendo un número muy grande (un tiempo con más de 10²⁵ dígitos, medido en segundos). ¡Como comparación, la edad del universo es de 4.3×10¹⁷ s, muchísimo más chico que el tiempo medio necesario para repetir la configuración de un gas en solo un metro cúbico! Por lo que el “casi siempre crece” de Boltzmann está bastante bien.

Además de Dr. Strange, muchas otras películas exploran la idea abominable de la eterna repetición (aunque no todas la consideran abominable). Les dejo algunas recomendadas para el fin de semana:

• El día de la marmota (1993)
• Corre Lola corre (1996)
• La llegada (2016)
• La chica que saltaba en el tiempo (2006, para los amantes del animé, está en Netflix)
• Beautiful dreamer (1984, también para amantes del animé)
• Triángulo (2009)

Ya están disponibles en la página de la teórica el video de la clase de ayer y los apuntes para la clase de mañana. Y no dejen de ver el post con las excelentes noticias de la práctica.

En la clase de ayer vimos el teorema del virial. Este es un teorema muy útil, tanto en la versión de Mecánica Estadística como en su versión de Mecánica Clásica. Pero también es un teorema que puede ser fácilmente aplicado a situaciones en las que no se cumplen sus hipótesis, para obtener cualquier resultado (“No lo se Rick, parece falso”). Recuerden que las partículas en el sistema deben estar confinadas por el potencial. A continuación les doy dos ejemplos de aplicaciones (aunque no les voy a dar la fórmula para fabricar materia oscura condensada, y todos sabemos que no es dos partes de quarks plutónicos, una parte de cesio, y una botella de agua).

Comencemos con el gas ideal. Habíamos visto que el teorema del virial puede escribirse como

donde los r son las posiciones de las partículas, F son las fuerzas sobre cada partícula, N es el número de partículas, y T la temperatura. La suma es sobre todas las partículas. Para un gas ideal, la única fuerza que tenemos está asociada a la presión P. Usando que la fuerza total, sumada sobre todas las partículas, es ∑ r · F = – ∫ r · n P dA (donde n es la normal externa a la pared, y dA el diferencial de superficie), después de hacer algunas cuentas se puede llegar (usando el teorema de Gauss) a que el término de la izquierda es 3PV (con V el volúmen). ¡Por lo que recuperamos la ecuación de estado de un gas ideal: PV = NkT!

Veamos ahora una aplicación más oscura. Consideremos un clúster de N galaxias (es decir, una acumulación de galaxias en el universo), cada una con masa m y con masa total M = Nm. Las galaxias en el cluster están confinadas por la fuerza gravitatoria. Nos conviene ahora escribir el teorema del virial, para una fuerza que decae como el cuadrado de la distancia, como

donde U es la energía cinética y V ahora es la energía potencial. Asumiendo que el clúster es esférico, para la fuerza gravitatoria V = -3GM²/(5R), donde G es la constante de gravitación universal, y R el radio del clúster. Por otro lado la energía cinética media es <U> = M<v²>/2. De estas dos relaciones podemos estimar la masa del clúster como

La velocidad cuadrática media de las galaxias se puede medir, por ejemplo, por corrimiento Doppler. Y la masa del cluster se puede estimar de forma independiente a esta fórmula a partir de la luminosidad del cluster. Y aquí comienzan los problemas: esta fórmula da una masa M mayor que la que se estima con la luminosidad, sugiriendo que falta una fracción de materia no que no estamos observando. Este argumento puede ser ampliado para considerar otras formas de energía (por ejemplo, la energía en el campo magnético de las galaxias y el clúster), pero no cambia el resultado central. Este no es el único argumento a favor de la existencia de materia oscura, pero en conjunto con otros nos indica que cerca del 85% de la materia en el universo tiene que ser materia oscura.

Stanislaw Lem fue un escritor polaco, autor de Solaris. El libro fue la base para el guión de la película Solaris (1972) dirigida por Andrei Tarkovsky (no estoy hablando de la remake de Hollywood). En Solaris, Lem imagina el oceano de un planeta que desarrolla en forma espontánea su propia conciencia (con un claro vínculo con los cerebros de Boltzmann de un post previo). Pero las novelas y cuentos de Stanislaw Lem tienen otros vínculos interesantes con la termodinámica y la mecánica estadística.

En Ciberíada, Lem escribe cuentos breves sobre las aventuras de dos constructores, Trurl y Clapaucio. Ambos tienen poderes y capacidad de construcción sobrehumanos. En una de las historias ambos son capturados por un pirata con un doctorado sediento de información. Para escapar, Trurl y Clapaucio construyen un demonio del segundo tipo (un demonio del primer tipo, para Lem, es un demonio de Maxwell, considerado una trivialidad por Trurl y Clapaucio). El demonio de Lem puede observar todas las moléculas de un gas en cada microestado posible, y extraer información de sus configuraciones. ¿Al fin y al cabo, siendo todos los microestados posibles, algunos microestados pueden corresponder a ordenamientos de las moléculas que revelen secretos insondables del universo, no?

“Si primero jura solemnemente, de arriba abajo y cruzando su corazón, que nos dejará ir, le daremos información, información sobre información infinita, es decir, le haremos su propio Demonio de Segundo Tipo, que es mágico y termodinámico, no-clásico y estocástico, y de cualquier viejo barril o estornudo extraerá información para usted sobre todo lo que fue, es, puede ser o será. ¡Y no hay demonio más allá de este Demonio, porque es del Segundo Tipo, y si lo quiere, dígalo ahora!“

Stanislaw Lem, Ciberíada (1965)

Pero, ¿qué es un demonio de Maxwell? Imaginemos un gas en un recinto, separado por un tabique. En el tabique agregamos una compuerta con un resorte, como se muestra en la siguiente figura:

En 1867, James Clerk Maxwell imaginó un demonio que podía conocer el estado de cada una de las partículas en el gas. Este demonio es puesto a controlar la compuerta de la figura. Cada vez que una molécula del lado B se acerca a la compuerta, el demonio observa su energía cinética. Si es grande, el demonio cierra la compuerta. Pero si su energía cinética es pequeña, el demonio abre la compuerta y deja pasar la molécula al recinto A. De esta forma, el demonio puede bajar la temperatura y disminuir la entropía del gas en el recinto A, violando (aparentemente) la segunda ley de la termodinámica.

La solución a esta paradoja está relacionada con que el proceso de medir, almacenar, y borrar información del estado de cada molécula requiere realizar trabajo. Los primeros argumentos contra el demonio de Maxwell, de Szilárd Y Brillouin en 1929, consideraban simplemente el trabajo asociado a medir la velocidad de cada molécula, y su costo energético. En este caso, considerando el sistema completo (el gas en ambos recintos y el demonio de Maxwell), la entropía crece y el segundo principio está salvado. Con el tiempo las restricciones en el mínimo de energía necesario para medir el estado de la molécula fueron bajando, y argumentos más modernos contra el demonio de Maxwell usan teoría de la información para estimar el costo energético de procesar la información adquirida por el demonio. Los que quieran aprender más sobre este tema pueden leer este excelente artículo, encontrado en cuatrimestres previos por Nahuel Freitas y Guillem Pérez Nadal:

Demons, Engines and the Second Law

Finalmente, ya están disponibles en la página de la teórica el video de la última clase, y los apuntes para la próxima clase.