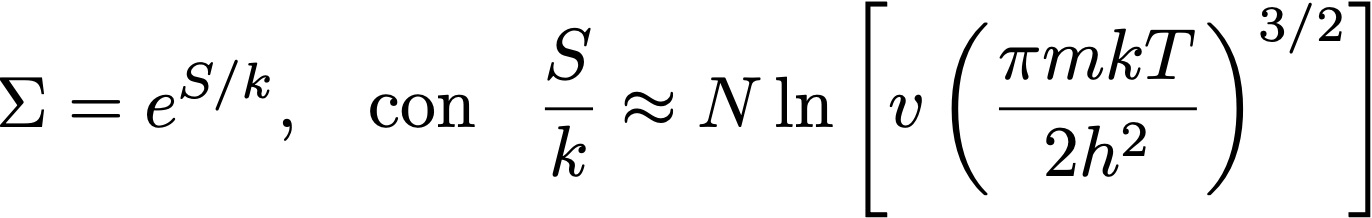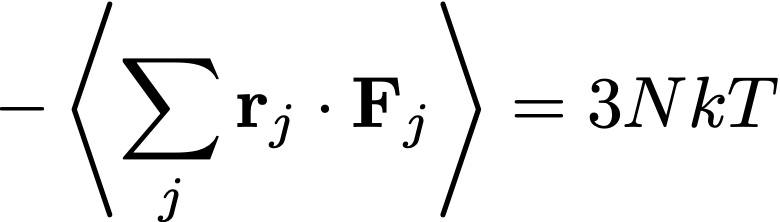“Ha llegado el momento de anunciar: Esta isla, con sus edificios, es nuestro paraíso privado. He tomado algunas precauciones -físicas, morales- para su defensa: creo que lo protegerán. Aquí estaremos eternamente -aunque mañana nos vayamos- repitiendo consecutivamente los momentos de la semana y sin poder salir nunca de la conciencia que tuvimos en cada uno de ellos.“

Adolfo Bioy Casares, La invención de Morel (1940).

La repetición eterna, como los espejos y la cópula para un heresiarca de Uqbar, es abominable (excepto tal vez para Friedrich Nietzsche). Probablemente nos parezca antinatural justamente porque nunca observamos en la naturaleza que las configuraciones de sistemas extensos se repitan exactamente de la misma forma. Esta observación fue una de críticas que Poincaré y Zermelo, entre otros, realizaron a la teoría estadística de Boltzmann. Imagino que Sísifo también tendría sus objeciones. Y a Dormammu tampoco le deben gustar las repeticiones:

En el teorema H de Boltzmann, su entropía casi siempre crece. Imaginemos un gas que ocupa la mitad de un recinto, separado en dos por un tabique. En un dado instante el tabique se retira, y el gas se expande hasta ocupar todo el recinto (con el consecuente aumento de la entropía). Dado que todas las configuraciones son equiprobables, en algún instante todas las moleculas del gas podrían estar en la primer mitad del recinto (al fin y al cabo, podemos tener configuraciones que incluyan a un cerebro de Boltzmann, ¿no?). Pero si en ese preciso instante volvemos a poner el tabique, recuperamos en forma espontánea la primera configuración, que tenía menor entropía. Este posible retorno a una configuración previa fue visto por Poincaré como un problema abominable para la teoría de Boltzmann (aunque más tarde Poincaré se convenció de su valor).

Efectivamente, si el número de configuraciones de un gas es discreto, existe una probabilidad no nula de que vuelva espontáneamente a una configuración previa (y si las configuraciones son contínuas, de que vuelva a una configuración arbitrariamente cercana a la configuración inicial). Pero el tiempo necesario para volver a encontrar esta configuración es increíblemente largo, lo que vuelve a este escenario irrelevante a fines prácticos. Estimemos esto para un metro cúbico de aire a temperatura ambiente (T = 300 K). Vimos que el número de configuraciones Σ de un gas ideal lo podemos calcular (en el ensamble microcanónico) como

donde S es la entropía, N el número de partículas, v el volúmen específico del gas, m la masa de las partículas (moléculas de N₂), k la constante de Boltzmann, y h la constante de Planck (ignoro un factor aditivo despreciable en la entropía). Usando valores típicos para estos parámetros (y considerando que v ≈ 5×10^-29 m³), obtenemos que el número de microestados o configuraciones posibles es

¡Este es un número enorme, con más de 10²⁵ dígitos! Asumamos ahora que las configuraciones cambian cada vez que hay un choque entre partículas. Es decir, cuando las partículas en el gas chocan, intercambian momento, y pasan de una configuración a otra. Para el aire a temperatura y presión ambiente, el tiempo entre choques es τ ≈ 10^-10 s. Y si todas las configuraciones son equiprobables, podemos estimar el tiempo medio para repetir una configuración como proporcional a Σ·τ, que sigue siendo un número muy grande (un tiempo con más de 10²⁵ dígitos, medido en segundos). ¡Como comparación, la edad del universo es de 4.3×10¹⁷ s, muchísimo más chico que el tiempo medio necesario para repetir la configuración de un gas en solo un metro cúbico! Por lo que el “casi siempre crece” de Boltzmann está bastante bien.

Además de Dr. Strange, muchas otras películas exploran la idea abominable de la eterna repetición (aunque no todas la consideran abominable). Les dejo algunas recomendadas para el fin de semana:

• El día de la marmota (1993)
• Corre Lola corre (1996)
• La llegada (2016)
• La chica que saltaba en el tiempo (2006, para los amantes del animé, está en Netflix)
• Beautiful dreamer (1984, también para amantes del animé)
• Triángulo (2009)

Ya están disponibles en la página de la teórica el video de la clase de ayer y los apuntes para la clase de mañana. Y no dejen de ver el post con las excelentes noticias de la práctica.

En la clase de ayer vimos el teorema del virial. Este es un teorema muy útil, tanto en la versión de Mecánica Estadística como en su versión de Mecánica Clásica. Pero también es un teorema que puede ser fácilmente aplicado a situaciones en las que no se cumplen sus hipótesis, para obtener cualquier resultado (“No lo se Rick, parece falso”). Recuerden que las partículas en el sistema deben estar confinadas por el potencial. A continuación les doy dos ejemplos de aplicaciones (aunque no les voy a dar la fórmula para fabricar materia oscura condensada, y todos sabemos que no es dos partes de quarks plutónicos, una parte de cesio, y una botella de agua).

Comencemos con el gas ideal. Habíamos visto que el teorema del virial puede escribirse como

donde los r son las posiciones de las partículas, F son las fuerzas sobre cada partícula, N es el número de partículas, y T la temperatura. La suma es sobre todas las partículas. Para un gas ideal, la única fuerza que tenemos está asociada a la presión P. Usando que la fuerza total, sumada sobre todas las partículas, es ∑ r · F = – ∫ r · n P dA (donde n es la normal externa a la pared, y dA el diferencial de superficie), después de hacer algunas cuentas se puede llegar (usando el teorema de Gauss) a que el término de la izquierda es 3PV (con V el volúmen). ¡Por lo que recuperamos la ecuación de estado de un gas ideal: PV = NkT!

Veamos ahora una aplicación más oscura. Consideremos un clúster de N galaxias (es decir, una acumulación de galaxias en el universo), cada una con masa m y con masa total M = Nm. Las galaxias en el cluster están confinadas por la fuerza gravitatoria. Nos conviene ahora escribir el teorema del virial, para una fuerza que decae como el cuadrado de la distancia, como

donde U es la energía cinética y V ahora es la energía potencial. Asumiendo que el clúster es esférico, para la fuerza gravitatoria V = -3GM²/(5R), donde G es la constante de gravitación universal, y R el radio del clúster. Por otro lado la energía cinética media es <U> = M<v²>/2. De estas dos relaciones podemos estimar la masa del clúster como

La velocidad cuadrática media de las galaxias se puede medir, por ejemplo, por corrimiento Doppler. Y la masa del cluster se puede estimar de forma independiente a esta fórmula a partir de la luminosidad del cluster. Y aquí comienzan los problemas: esta fórmula da una masa M mayor que la que se estima con la luminosidad, sugiriendo que falta una fracción de materia no que no estamos observando. Este argumento puede ser ampliado para considerar otras formas de energía (por ejemplo, la energía en el campo magnético de las galaxias y el clúster), pero no cambia el resultado central. Este no es el único argumento a favor de la existencia de materia oscura, pero en conjunto con otros nos indica que cerca del 85% de la materia en el universo tiene que ser materia oscura.

Stanislaw Lem fue un escritor polaco, autor de Solaris. El libro fue la base para el guión de la película Solaris (1972) dirigida por Andrei Tarkovsky (no estoy hablando de la remake de Hollywood). En Solaris, Lem imagina el oceano de un planeta que desarrolla en forma espontánea su propia conciencia (con un claro vínculo con los cerebros de Boltzmann de un post previo). Pero las novelas y cuentos de Stanislaw Lem tienen otros vínculos interesantes con la termodinámica y la mecánica estadística.

En Ciberíada, Lem escribe cuentos breves sobre las aventuras de dos constructores, Trurl y Clapaucio. Ambos tienen poderes y capacidad de construcción sobrehumanos. En una de las historias ambos son capturados por un pirata con un doctorado sediento de información. Para escapar, Trurl y Clapaucio construyen un demonio del segundo tipo (un demonio del primer tipo, para Lem, es un demonio de Maxwell, considerado una trivialidad por Trurl y Clapaucio). El demonio de Lem puede observar todas las moléculas de un gas en cada microestado posible, y extraer información de sus configuraciones. ¿Al fin y al cabo, siendo todos los microestados posibles, algunos microestados pueden corresponder a ordenamientos de las moléculas que revelen secretos insondables del universo, no?

“Si primero jura solemnemente, de arriba abajo y cruzando su corazón, que nos dejará ir, le daremos información, información sobre información infinita, es decir, le haremos su propio Demonio de Segundo Tipo, que es mágico y termodinámico, no-clásico y estocástico, y de cualquier viejo barril o estornudo extraerá información para usted sobre todo lo que fue, es, puede ser o será. ¡Y no hay demonio más allá de este Demonio, porque es del Segundo Tipo, y si lo quiere, dígalo ahora!“

Stanislaw Lem, Ciberíada (1965)

Pero, ¿qué es un demonio de Maxwell? Imaginemos un gas en un recinto, separado por un tabique. En el tabique agregamos una compuerta con un resorte, como se muestra en la siguiente figura:

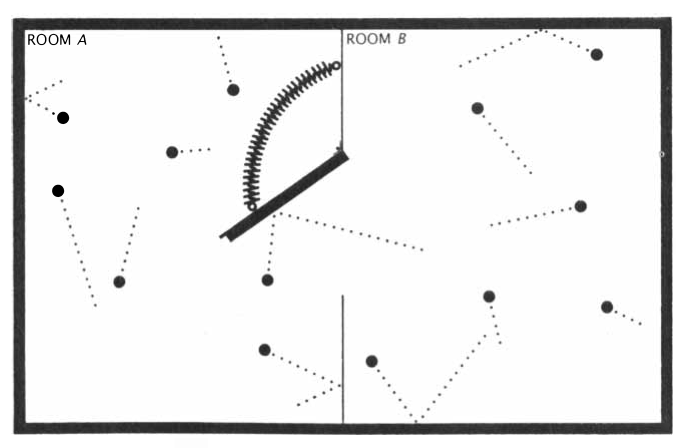
En 1867, James Clerk Maxwell imaginó un demonio que podía conocer el estado de cada una de las partículas en el gas. Este demonio es puesto a controlar la compuerta de la figura. Cada vez que una molécula del lado B se acerca a la compuerta, el demonio observa su energía cinética. Si es grande, el demonio cierra la compuerta. Pero si su energía cinética es pequeña, el demonio abre la compuerta y deja pasar la molécula al recinto A. De esta forma, el demonio puede bajar la temperatura y disminuir la entropía del gas en el recinto A, violando (aparentemente) la segunda ley de la termodinámica.

La solución a esta paradoja está relacionada con que el proceso de medir, almacenar, y borrar información del estado de cada molécula requiere realizar trabajo. Los primeros argumentos contra el demonio de Maxwell, de Szilárd Y Brillouin en 1929, consideraban simplemente el trabajo asociado a medir la velocidad de cada molécula, y su costo energético. En este caso, considerando el sistema completo (el gas en ambos recintos y el demonio de Maxwell), la entropía crece y el segundo principio está salvado. Con el tiempo las restricciones en el mínimo de energía necesario para medir el estado de la molécula fueron bajando, y argumentos más modernos contra el demonio de Maxwell usan teoría de la información para estimar el costo energético de procesar la información adquirida por el demonio. Los que quieran aprender más sobre este tema pueden leer este excelente artículo, encontrado en cuatrimestres previos por Nahuel Freitas y Guillem Pérez Nadal:

Demons, Engines and the Second Law

Finalmente, ya están disponibles en la página de la teórica el video de la última clase, y los apuntes para la próxima clase.

En la página de la teórica ya están disponibles el video de la última clase, y los apuntes para la próxima clase.

La lírica de la canción que acompaña a este post, del disco The Dark Side of the Moon, tiene la memorable frase “Money, it’s a gas“. Y aparentemente no es solo una licencia poética. Los que tengan curiosidad sobre cómo se usan herramientas de mecánica estadística para el estudio de economía y finanzas pueden mirar este muy buen review:

Colloquium: Statistical mechanics of money, wealth and income

que fue publicado en Reviews of Modern Physics en 2009. El artículo es introductorio y explica varios de los conceptos que se usan comúnmente en el área de econofísica, incluyendo modelos estocásticos, cómo se usa el ensamble canónico (o de Gibbs), los vínculos asociados a la “conservación del dinero” o para sistemas en los que pueden existir deudas, y cómo esto resulta en diferentes equilibrios estadísticos. En particular, la Sección I, y la Sección II (desde la subsección A hasta la C) se leen fácilmente, y usan muchos de los conceptos que introdujimos hasta ahora en la materia. En particular, en las secciones II.B y II.C, los autores reemplazan el vínculo de la energía por un vínculo sobre el dinero total circulante, y vuelven a obtener la distribución de probabilidad del ensamble canónico, pero donde ahora la temperatura es reemplazada por el promedio de dinero que tiene cada individuo.

Este artículo tiene también un hallazgo interesante sobre la visión amplia que tenía Boltzmann, que más de 100 años atrás vislumbró la aplicabilidad de la mecánica estadística tanto en física como en otras áreas. En 1905 Boltzmann, hablando sobre la generalización y formalización de la mecánica estadística realizada por Gibbs, escribió:

“Esto abre una perspectiva amplia, si no pensamos solamente en objetos mecánicos. Consideremos aplicar este método a la estadística de seres vivos, de la sociedad, en sociología, etc.”

Los que quieran mirar un ejemplo más reciente de este tipo de aplicaciones, pueden leer este artículo en Nature Communications sobre eventos extremos en sistemas macroeconómicos.