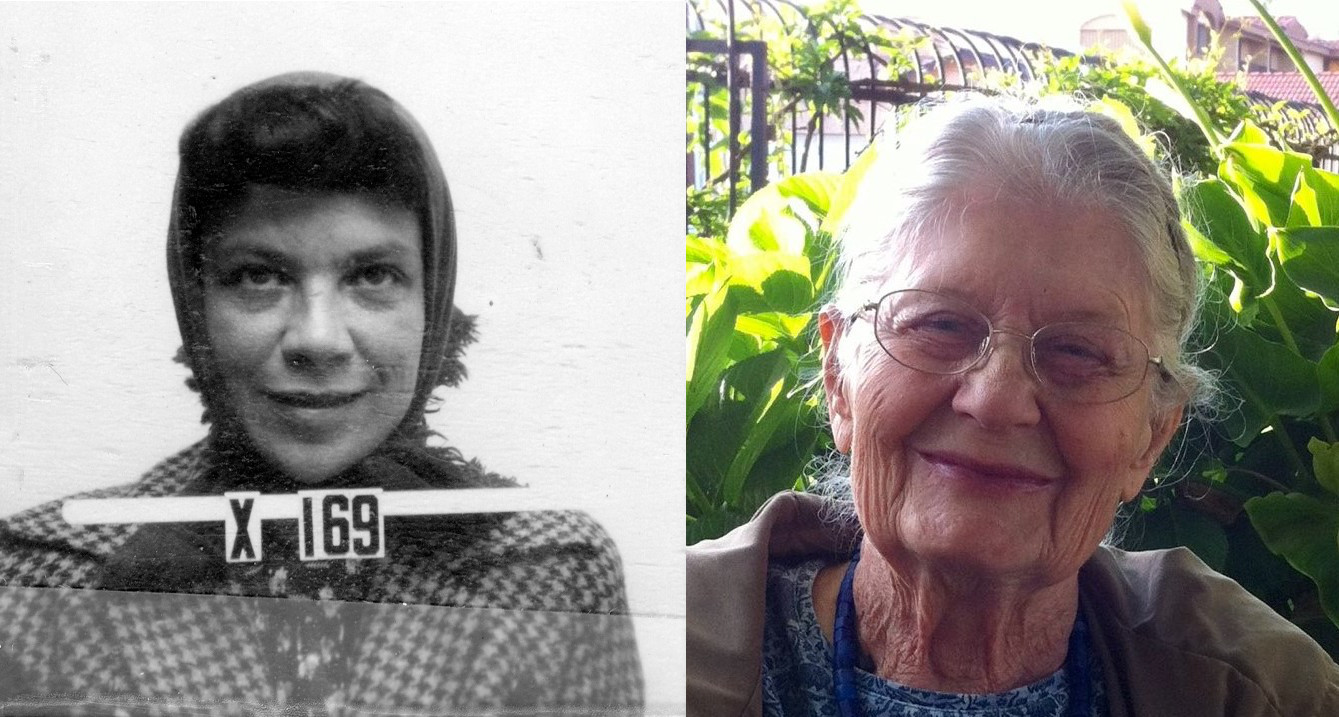La mecánica estadística, que nació a fines del siglo XIX y principios del siglo XX a partir de los trabajos de Boltzmann, Maxwell y Gibbs, tuvo un rol importante durante la Segunda Guerra Mundial. El proyecto Manhattan, que entre 1939 y 1946 reunió a varios de los científicos más brillantes de la época, usó frecuentemente sus herramientas e impulsó el desarrollo de métodos que ampliaron enormemente su área de aplicación. En las últimas clases comenzaron a aparecer métodos, y diversos nombres de científicos, que estuvieron relacionados con el proyecto Manhattan. Así que vamos a dedicar este post a algunos de ellos. El proyecto Manhattan tuvo como objetivo fabricar armas nucleares para los Estados Unidos durante la guerra. Jugó un rol central en el fin de la guerra del Pacífico, mostró lo que puede hacer la colaboración científica a gran escala, y generó desarrollos rápidos e importantes. Pero aún hoy se sigue discutiendo la necesidad de bombardear Hiroshima y Nagasaki, o la carrera armamentista nuclear que siguió a continuación. Sobre esa época, y para reflexionar sobe esos temas, les aconsejo “Dr. Strangelove, or How I Learned to Stop Worrying and Love the Bomb” (1964), una película satírica de Stanley Kubrick en la que el genial Peter Sellers tiene tres papeles (el presidente de los Estados Unidos, un capitán británico, y el científico nazi Dr. Strangelove).
En la última clase vimos el método de campo medio para el problema de Ising desarrollado por Hans Bethe. Bethe publicó este resultado en 1935, el año en que se mudó a los Estados Unidos (pueden ver el paper original aquí). Bethe trabajó en el proyecto Manhattan y luego en el desarrollo de la bomba de hidrógeno junto con Edward Teller y Stanislaw Ulam (yo tuve la suerte de conocer y hablar varias veces con Stirling Colgate, que trabajó con Teller y Bethe en este proyecto; probablemente el apellido les resulte de conocido de algún lado). Luego Bethe trabajó en la formación de elementos químicos por fusión nuclear en el interior de las estrellas, por el que ganó el premio Nobel en 1967. La mecánica estadística jugó roles importantes en estos trabajos. Pero su paper más famoso es un paper en el que no trabajó. En 1948, luego de la guerra, Ralph Alpher y George Gamow escribieron un trabajo sobre la formación de los primeros átomos en el universo. Gamow, al enterarse que el paper iba a salir publicado el 1 de abril (“April fools’ day“, el equivalente a nuestro día de los inocentes), agregó a Hans Bethe como segundo autor. Así, el paper de Alpher, Bethe y Gamow se volvió conocido como el paper α-β-γ (alfa, beta y gama). Más tarde, cuando Ralph Alpher trabajó con Robert Herman en el cálculo de la temperatura de la radiación cósmica de fondo, Gamow quiso convencer a Herman de que cambiara su apellido por “Delter”, para poder escribir un paper con autores Alpher, Bethe, Gamow y Delter (α-β-γ-δ). Herman se negó rotundamente.
El método de Montecarlo que se usa para resolver numéricamente el modelo de Ising también fue creado durante el proyecto Manhattan. Muchas veces se dice que Stanislaw Ulam inventó al método tal como lo conocemos hoy mientras trabajaba en el proyecto de la bomba atómica. Sin embargo, el método fue el resultado del trabajo conjunto de varias personas, que formaban parte de un grupo liderado por Nicholas Metropolis, y entre las que se encontraban Ulam, John von Neumann, Edward Teller, Augusta H. Teller, Marshall Rosenbluth y Arianna W. Rosenbluth. Casualmente los Teller (Edward y Augusta) se mudaron de su Hungría natal a Estados Unidos en 1935, antes de la segunda guerra mundial, por invitación de George Gamow (el del paper α-β-γ), mostrando cómo todo se conecta con todo.
Es muy probable que la idea original para el método de Montecarlo haya nacido de von Neumann y Ulam. Y que los Teller y los Rosenbluth (dos parejas de físicos) hicieran el grueso del trabajo, desarrollado las ideas e implementando el código numérico para poder probarlo en MANIAC I, una de las primeras computadoras de Los Alamos. En particular, hoy sabemos que el trabajo de Augusta Teller y de Arianna Rosenbluth fue central, aunque en aquella época no fue tan valorado. Augusta Teller escribió la primera versión del programa de Montecarlo para MANIAC I, mientras que Arianna Rosenbluth fue la encargada de escribir el programa definitivo (¡en código de máquina!) que fue usado para calcular, usando mecánica estadística, la difusión de neutrones en el material para la fisión nuclear, y más tarde (luego de terminada la guerra) para calcular los resultados sobre el algoritmo que se reportaron en los papers. Lamentablemente los prejuicios de la época, y el hecho de que ambas dejaran de ejercer su profesión para dedicarse a sus familias, hicieron que no recibieran el crédito merecido y que quedasen pocos documentos y fotos de ellas:
Luego de la guerra, Metropolis y Ulam publicaron el primer paper no clasificado explicando el método en detalle. Y más tarde Metropolis, Marshall y Arianna Rosenbluth, y Edward y Augusta Teller publicaron otro paper, famoso y que usualmente se considera la referencia para el algoritmo. Hoy el método de Montecarlo se usa para resolver en forma numérica una gran variedad de problemas en física y en ciencia de datos, y es central en el modelado de problemas de mecánica estadística.
Los que quieran leer más sobre Arianna W. Rosenbluth, y sobre el desarrollo del método de Montecarlo, pueden mirar estos links:
- El obituario de Arianna Rosenbluth en The New York Times: tiene muchos detalles interesantes sobre su carrera, incluyendo el hecho de que Felix Bloch se negó a tomarla como estudiante doctoral porque él no trabajaba con estudiantes mujeres.
- Un paper en Physics of Plasmas sobre la creación del método de Montecarlo tal como lo contó Marshall Rosenbluth en un congreso, en el que también destaca el rol de Arianna. El paper tiene una breve (pero clara) descripción del método.
Los que quieran leer más historias sobre el proyecto Manhattan pueden mirar también las memorias de Richard Feynman (¡incluyen lecciones sobre como abrir cajas fuertes!):
Y no dejen de mirar este importante posteo de la práctica sobre la guía computacional (¡justamente, usando el método de Montecarlo!). La próxima práctica estará dedicada a este tema, y tienen hasta el 9/7 para entregar la guía. ¡Y recuerden que antes del 20 de junio tienen que completar la encuesta!