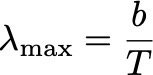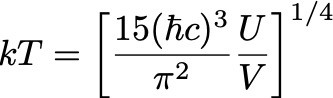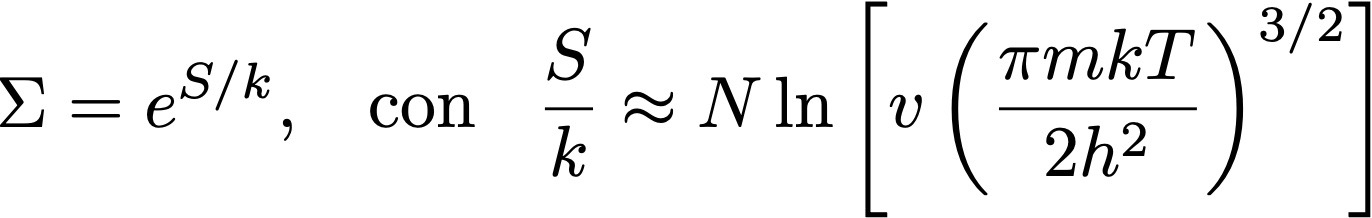Todos los cuerpos absorben radiación electromagnética, y emiten espontáneamente una parte en forma de radiación en equilibrio térmico con el cuerpo (es decir, como fotones a la misma temperatura que la fuente térmica). Esa es la radiación de cuerpo negro. Arnold Schwarzenegger sabe mucho sobre esto, y se cubre en barro frío cada vez que tiene que luchar contra un depredador, porque estos aliens pueden ver la radiación emitida por su cuerpo. Pero todos emitimos esta radiación, no solo Arnold (la radiación no depende de cuantas horas pasemos en el gimnasio). Así que en este post vamos a ver cómo esto se puede usar para saber qué temperatura tienen las personas en los aeropuertos, y también para saber qué temperatura tiene el universo.
¿En qué longitud de onda emite radiación de cuerpo negro una persona a 36 grados Celsius? A partir del espectro de Planck se puede ver que la máxima emisión ocurre para una longitud de onda que sigue la ley de Wien,
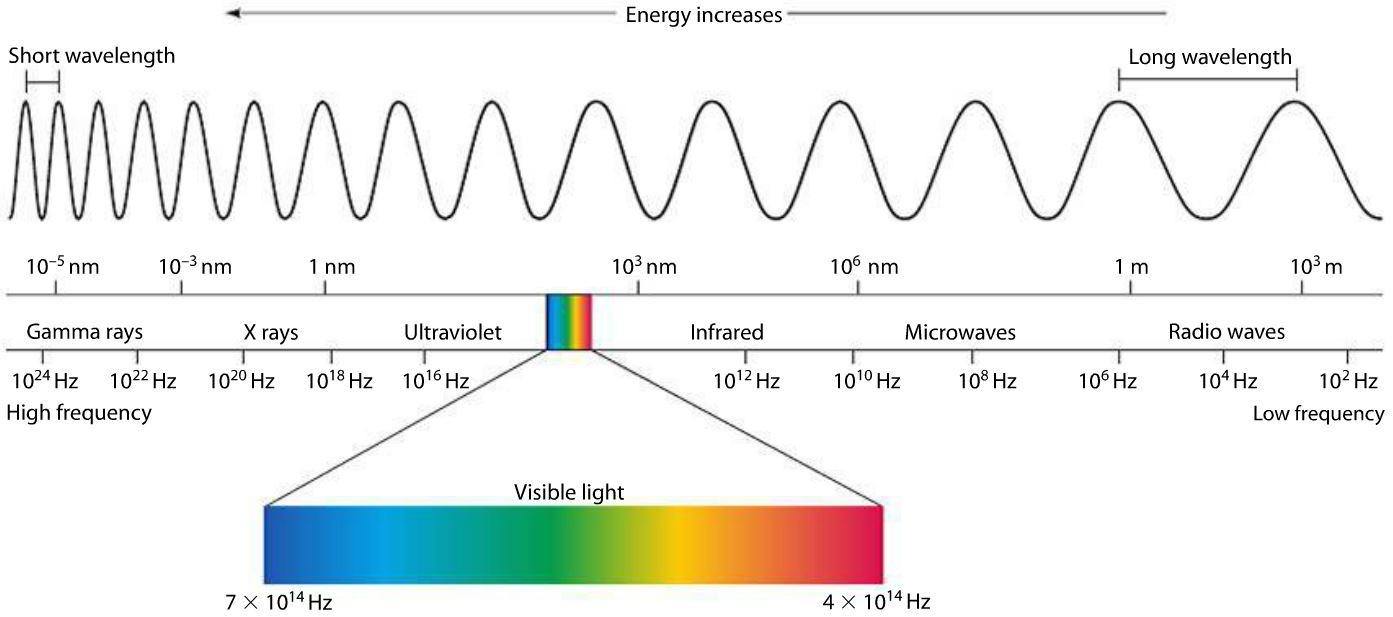
donde b = 2898 μm K. Noten que esto significa que al cambiar la temperatura del cuerpo, cambia el “color” de la radiación electromagnética emitida, ya que el color depende del espectro emitido (y fuertemente de en qué longitud de onda está el pico del espectro). Entonces ¿en qué longitud de onda debe observar una cámara para detectar este tipo de radiación? Para 36 grados Celsius, T= 309 K, y λmax ≈ 9.4 μm. De hecho, si variamos la temperatura entre 30 y 40 grados Celsius, el máximo del espectro varía respectivamente entre 9.56 y 9.26 μm (o entre 9560 y 9260 nm). Esto corresponde a radiación electromagnética infraroja. ¡Así que mirando los colores en una cámara infrarroja podemos estimar la temperatura de los cuerpos! Y así también sabemos en qué región del espectro electromagnético funcionan los ojos del depredador que persigue a Schwarzenegger:
Sabiendo esto, ¿a qué temperatura se encuentra la radiación cósmica de fondo? Estamos rodeados por radiación electromagnética de cuerpo negro que fue emitida en el momento en que se formaron los primeros átomos en el universo, y que llega a nosotros proveniente de todas las direcciones. Esta radiación corresponde a fotones que se desacoplaron de la materia en la época de recombinación: el momento en que la temperatura del universo bajó lo suficiente como para que protones y electrones pudieran combinarse formando átomos de hidrógeno (eléctricamente neutros), aproximadamente 370.000 años luego del Big Bang, y cuando el universo estaba una temperatura media de unos 3000 K. Antes, el campo electromagnético interactuaba con la materia, mientras que luego de la recombinación los fotones de la radiación cósmica de fondo dejaron de interactuar (básicamente, porque la radiación electromagnética dejó de sufrir scattering con los electrones libres). ¡Como resultado, la radiación cósmica de fondo que vemos hoy es un gas de fotones en equilibrio térmico con la materia que formaba el universo hace 13.771.700.000 años!
En 1964, Arno Penzias y Robert Wilson, realizando mediciones con una antena en los Laboratorios Bell, encontraron una extraña señal de microondas con un máximo en λmax ≈ 1 mm. Esa señal captada por la antena corresponde a este gas de fotones, mensajero del universo temprano. Usando nuevamente la ley de Wien podemos ver que esta longitud de onda corresponde a T ≈ 2.7 K (la temperatura determinada originalmente por Penzias y Wilson en 1964 era ligeramente mayor, por la incerteza experimental del instrumento). Esa temperatura corresponde a la temperatura media del gas de fotones que forma la radiación cósmica de fondo. Y no es 3000 K, sino alrededor de 1000 veces menor por la expansión del universo, que resulta también en la expansión del gas y en una disminución de la temperatura a medida que el universo envejece. Porque la temperatura T de un gas de fotones cumple la ecuación
donde U es su energía total, y V el volumen ocupado por el gas. A mayor volumen, menor temperatura.
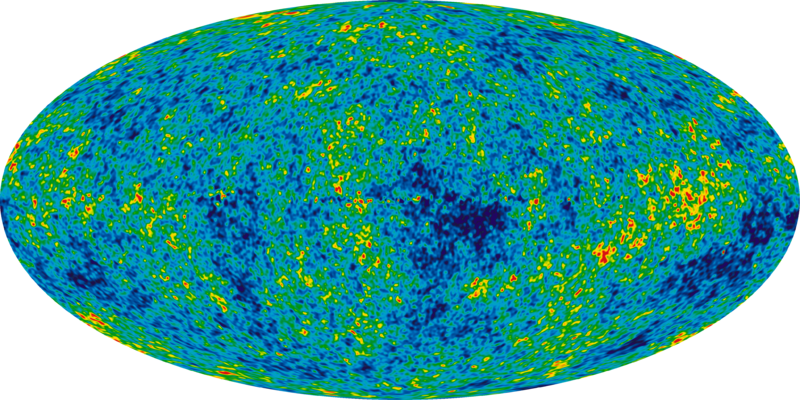
Penzias y Wilson midieron la temperatura media de esta radiación. Pero hoy sabemos que la temperatura de este gas de fotones no es perfectamente isótropa, y que su anisotropía (es decir, su pequeña variación cuando miramos en diferentes direcciones en el universo) nos brinda información sobre el universo temprano. Cuando se resta el valor medio a la radiación, la proyección de las fluctuaciones en la potencia de la radiación que nos llega de diferentes regiones del firmamento se ve así:
Pero esta es otra historia.