Ahora que he malhecho su atención con un título burlesco y un verbo de dudosa existencia, permítanme aclararles que lo que vine a decirles no está relacionado directamente con el parcial, salvo que es a las 10:30 en el aula de clases. Lo que sigue es para completar la clase del jueves pasado. En esa clase encontramos la transformación a las variables de ángulo-acción para un pozo cuadrado de potencial en una dimensión, es decir, una partícula rebotando entre dos paredes. Como el movimiento es esencialmente el de una partícula libre, las coordenadas ángulo-acción conservan el carácter ortogonal y cartesiano de las variables impulso y posición. O sea: de una cuadrícula en el plano x-p pasamos a la misma cuadrícula pero con otros nombres para las variables canónicas. En clase notamos que bastaba  ’redondear’ un poco el potencial para curvar las líneas coordenadas del nuevo sistema, pero no hicimos ningún cálculo explícito.

Lo que se muestra en los siguientes videos es la transición entre el sistema de coordenadas ángulo-acción para un potencial 1D que se altera paulatinamente desde V(x) = |x|, hasta V(x) igual al pozo infinito,  pasando por el potencial del oscilador armónico. El potencial es de tipo exponencial. La primera imagen ilustra todo el rango de exponentes considerados, entre 1 y 150.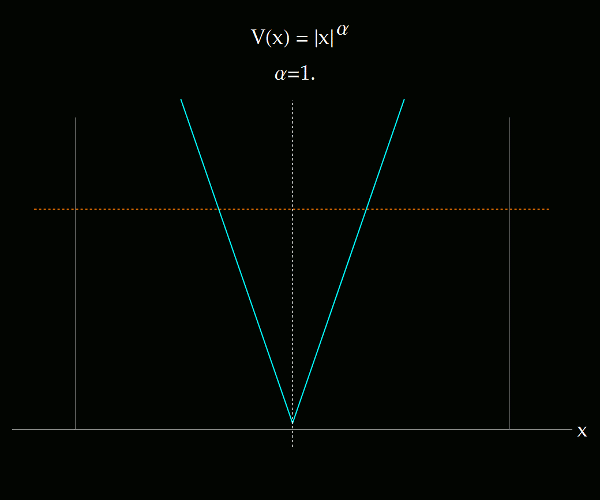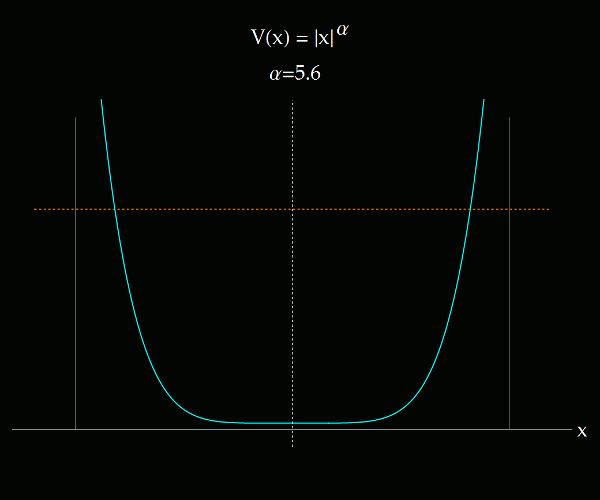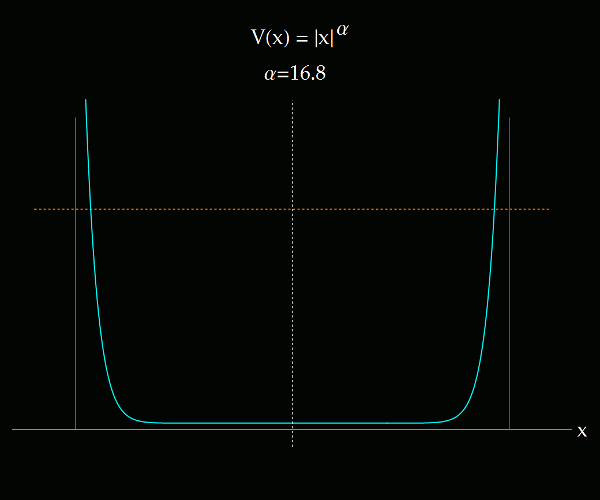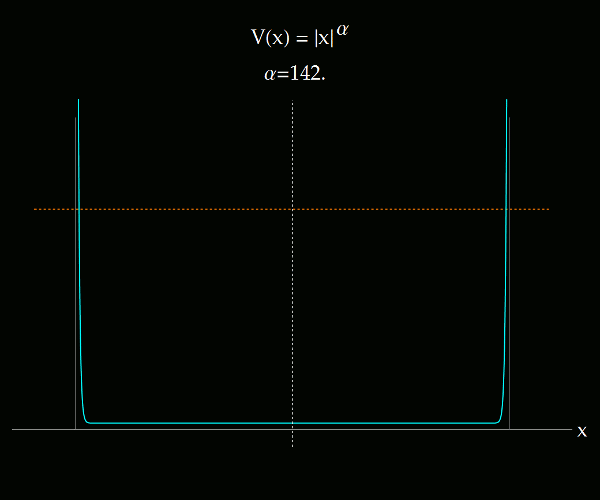

Para cada valor de α hay un sistema de coordenadas canónicas ángulo-acción que definen en el plano x-p sus propias curvas coordenadas. Las curvas coordenadas asociadas a la variable angular son típicamente radiales; las asociadas a la variable acción rodean al origen. Cuando el potencial tiende al pozo infinito, salvo para energías muy bajas (donde la partícula aún es sensible a la parte suave del potencial), las curvas coordenadas de las variables ángulo-acción tienden a la cuadrícula definida por las variables x-p. Vedlo en el siguiente video (con audio tenebroso). Recomiendo verlo en pantalla completa.

Las curvas coordenadas de la variable ángulo están numeradas como las horas del día.

En el segundo video se muestra una trayectoria en el espacio de fases para un valor intermedio del exponente α. La partícula cae desde el extremo x > 0 y se mueve sobre una de las curvas de energía constante. Sobre la trayectoria en el plano x-p están marcados 24 puntos que corresponden a 24 valores equiespaciados de la variable ángulo. La partícula tarda el mismo tiempo en moverse entre puntos consecutivos: esa es la propiedad que define a las variables de ángulo-acción, la isocronía. Esta vez con un audio luminoso, y también para ver en pantalla completa: