• En primer lugar, un apunte con el problema resuelto durante la clase del lunes pasado. Es el problema 20 de la guía 7. Para bajar [aquí]. Apenas 8 páginas entre enunciado, figuras, solución y espacios en blanco. Nuestra consigna es “salvemos a los bosques”.
• Los problemas de la Guía 7 acerca de las variables de ángulo-acción pertenecen todos a la misma especie. Goldstein los despacha en media docena de ecuaciones. La práctica requiere, sin embargo, un proceso de familiarización. Pero, una vez cumplido, todos los problemas se resuelven más o menos en los mismos 3 o 4 pasos. Esos pasos están explicados con todo detalle en [este apunte]. Un mamotreto de 24 páginas a todo color cuya impresión arrastrará consigo más de una hectárea de bosque tropical.
• Siempre la parte más interesante de estos problemas es ver con qué diseño nos sorprenden las curvas coordenadas de las variables de ángulo-acción. Abajo, por ejemplo, está el caso del movimiento radial de Kepler.
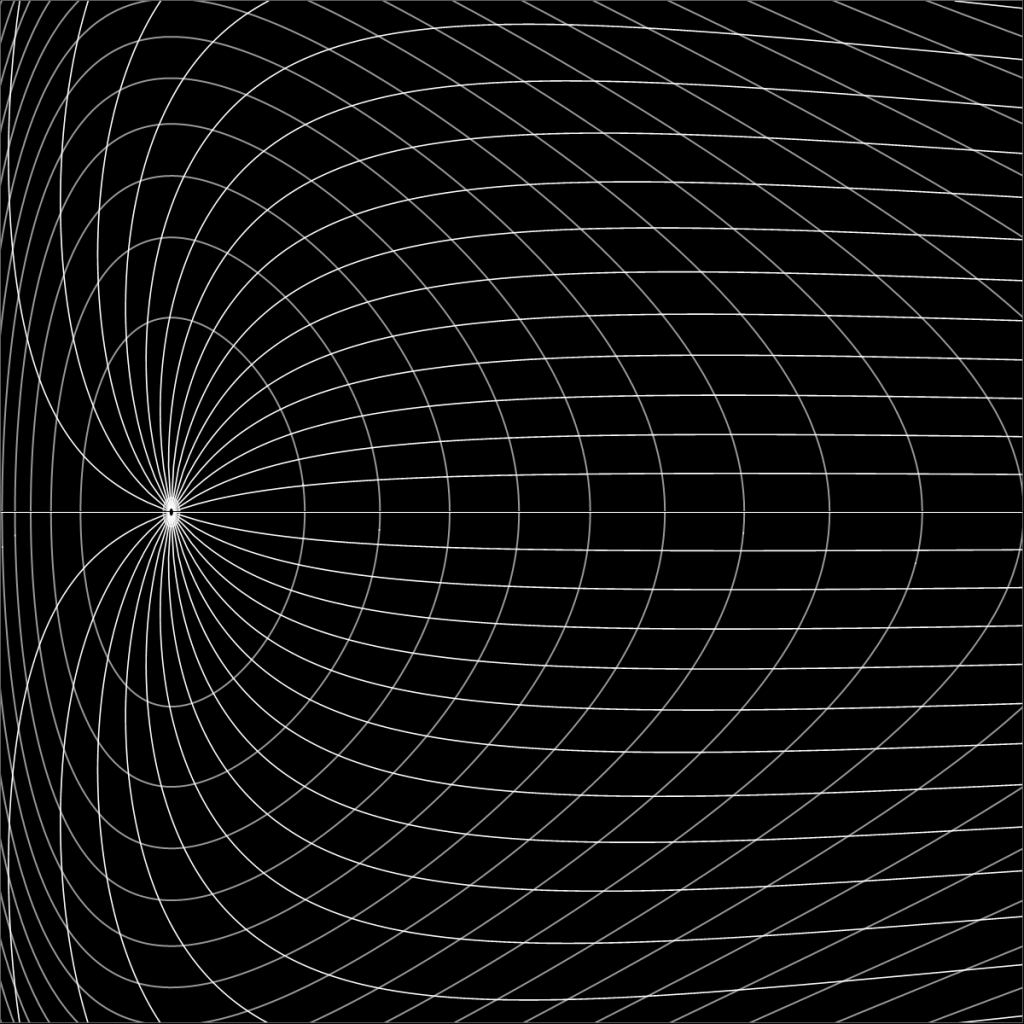
• Es un simple ejercicio demostrar que la variable ángulo asociada al movimiento radial acotado del problema de Kepler (exceptuando la órbita circular) coincide a menos de un factor con el área barrida por el radio vector. ¿Se acuerdan de la ley áreas iguales en tiempos iguales? En este sentido, el avance de la variable ángulo de la Tierra durante un día es siempre el mismo, en tanto que el avance del ángulo que define su posición sobre la órbita (el ángulo de las coordenadas polares) depende del día.
• Y es una notable falta que en la mayoría de los libros se omita decir que las variables de ángulo-acción, al menos en los problemas unidimensionales, no son más difíciles de entender que las coordenadas polares en el plano. Las transformaciones canónicas permiten cambios de variables tan extraños que es comprensible no entender qué significan, por ejemplo, las nuevas coordenadas Q = Log[sin p/q] y P = q ctg p. Pero esto no es excusa en el caso de las variables de ángulo-acción.
• No todos los retratos de fase son simétricos respecto al eje q. Es muy fácil hacer transformaciones canónicas que deformen el retrato de fase hasta llevarlo a formas fantásticas. Un caso que brilla por su falta de espectacularidad, pero que sirve para presentar esta cuestión, es el de una rotación en el plano qp. Con esta transformación el retrato de fase del oscilador, por ejemplo, toma típicamente el siguiente aspecto. En este caso es H = p² + p q + q². ¿Cómo se escriben en este caso las integrales que definen a la función característica de Hamilton y a la variable ángulo? ¿Cuáles son los puntos de retorno? ¿Cómo hay que dividir la órbita para que en cada tramo queden funciones univaluadas de q? Eh.
• Las variables de ángulo-acción de navidades pasadas (la notación cambió levemente): [2017 2c], [2018 1c], [2018 2c].
• Un libro en donde se toman la molestia de dar algunos ejemplos del cálculo de las variables de ángulo-acción: el de Percival y Richards (a la teoría la encaran por otro lado).

Ahora toca responder a ciertas graves denuncias que se han hecho circular en el aula.

• El problema 9 de la Guía 7 no tiene ningún error. No se dice nada de la dependencia explícita de f con el tiempo simplemente porque no tiene importancia decirlo.
• En el problema 3 es cierto que falta aclarar que es la componente z del momento angular la que se conserva.
• El problema 16 se resuelve por separación de variables. Busquen W(q₁, q₂) = W₁(q₁) + W₂(q₂). Contrariamente a lo que sugiere el enunciado, no intenten calcular las integrales. Resuelvan todo lo que se les dice, pero dejen sus resultados en términos de expresiones integrales. La parte interesante es la pregunta final.
• En el problema 17, en la expresión del hamiltoniano, E tiene que aparecer con signo menos. (Se editó el cambio en la guía que está subida).
• En el problema 18, si les queda una integral al cuadrado, pues les queda una integral al cuadrado. No hay ningún signo mal.
• Supongo que no avanzaron más allá, porque hasta ese problema me hicieron consultas.
• Y todavía falta subir la guía de relatividad.