Al hablar sobre el hombre araña algunas personas querrán fotos y otras pensarán en multiversos. Sin embargo, está claro (?) que la mayoría va a pensar en la mejor versión del héroe de Marvel: el Julián Álvarez de 2021.
En cualquier deporte la técnica juega un rol fundamental: esta se puede definir como la economía temporal del movimiento, y, por este motivo, disponer de una buena técnica representa una ventaja muy grande en cualquier disciplina que requiera resolver situaciones en tiempos y/o espacios reducidos. En particular, en el video, se puede ver como el jugador recibe un pelotazo largo con una pierna y le pega con la otra, haciendo todo muy rápido y de manera fluida.
Los sistemas físicos en la mecánica clásica también siguen un patrón similar. Al mejor estilo F1, la dinámica de un sistema clásico se describe mediante las ecuaciones de Newton. Luego, vimos que la descripción dinámica puede hacerse a través del lagrangiano, recuperando la misma dinámica que con Newton, pero con ciertas ventajas operacionales.
Para describir la dinámica del sistema con el lagrangiano se usan las ecuaciones de Euler-Lagrange. Estas ecuaciones pueden seguirse desde las de Newton, junto con el principio de los trabajos virtuales, y algunas hipótesis más, pero también se pueden obtener partiendo de un principio fundamental: el principio de mínima acción.
Este principio dice que la evolución dinámica de los grados de libertad de un sistema físico, desde un tiempo inicial hasta otro final, es aquella que hace extrema una cierta cantidad, llamada casualmente “acción”. La acción se define como la integral temporal del lagrangiano, integrando desde el tiempo inicial hasta el final.

En este caso, S es la acción, y L es el lagrangiano. Se puede ver que este sistema dispone de un único grado de libertad, representado por la coordenada generalizada “x”. Digamos algunas cosas técnicas:
- La acción es una funcional, es decir, es una función de funciones. Esto es así debido a que, para calcular la acción, es necesario escribir explícitamente la dependencia temporal de las coordenadas generalizadas. En el ejemplo, para poder hacer la integral necesitamos tener x(t) (y por derivación dx/dt) y reemplazar estos valores en el lagrangiano. De esta forma tenemos todo en función del tiempo y podemos hacer la integral. Entonces el valor de S depende de las funciones q(t), es decir, de la dinámica de las coordenadas generalizadas.
- Por lo dicho anteriormente, para calcular un valor de la acción necesitamos conocer la evolución temporal de todos los grados de libertad del sistema. Ustedes ya vieron que variando la acción, salvo en el punto inicial y final, se obtienen las ecuaciones de E-L. Es decir, al “pedirle” a los grados de libertad que evolucionen de forma tal que hagan que la acción sea extrema, las coordenadas generalizadas “prefieren” evolucionar según las ecuaciones de E-L.
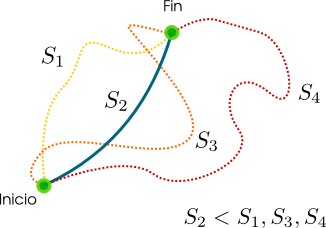
Este concepto no solo aparece en la mecánica clásica. De hecho, cualquier funcional S definida de forma similar será extrema cuando las funciones de las que dependa cumplan las ecuaciones de Euler Lagrange. De esta forma se puede calcular, por ejemplo, la curva que minimiza la distancia en cualquier geometría (seguramente en la guía de ejercicios les piden encontrar la curva que minimiza la distancia al desplazarse sobre un cilindro, por ejemplo).
Volviendo a la técnica deportiva, parece conceptualmente interesante discutir si la mejor forma de llevar a cabo un gesto técnico, tal como recibir la pelota, sea tal que minimice alguna funcional. Por ejemplo, en el próximo video se puede ver como con un movimiento muy simple, Matías Suárez simplifica la jugada de forma sublime. ¿Habrá hecho completa la guía 2 de mecánica clásica?
Viéndolo de esta forma, podríamos pensar que lxs jugadorxs de jerarquía son aquellxs que constantemente buscan minimizar esta funcional abstracta y desconocida, y que podemos aprender física en cualquier momento y en cualquier lugar!
P.d: en vísperas del superclásico, y sin la intención de mostrar favoritismo por alguno de los equipos, además de poner un video en el que aparece Belgrano, dejo también un lindo gol de boca. Para no quedar mal, je.


 Follow
Follow