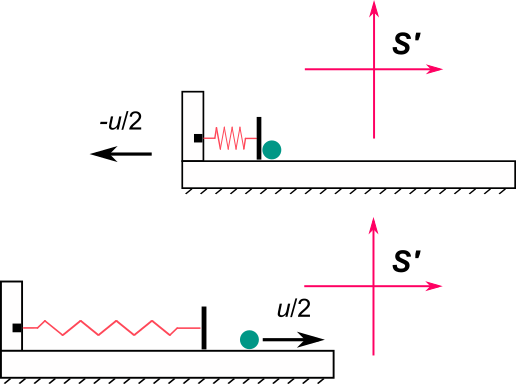
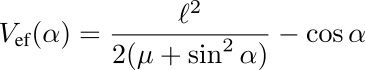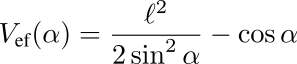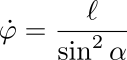En la clase de ayer vimos el problema 8 de la guía 1. Una partícula se mueve sobre un aro vertical que puede rotar alrededor del eje z, como muestra la animación de abajo.
Usamos las coordenadas generalizadas α y φ que muestra la siguiente figura:
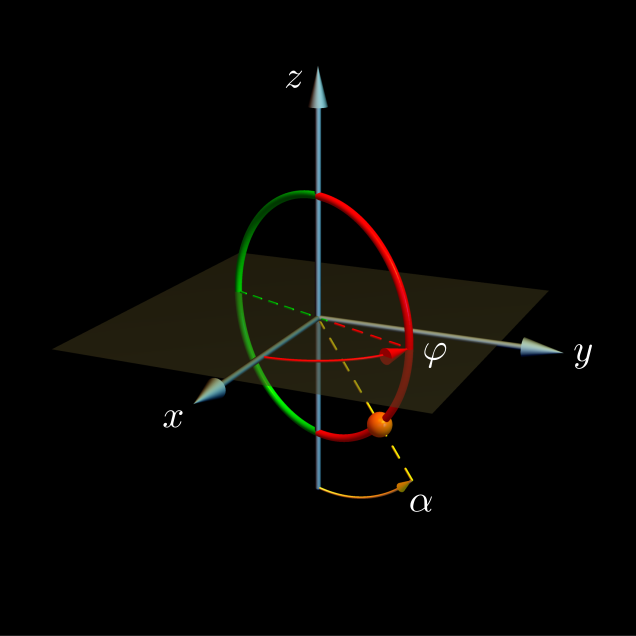
Llegamos a escribir el potencial efectivo, pero no hubo tiempo de analizar los tipos de movimiento posibles: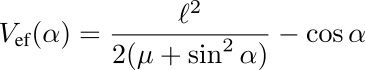
Aquí μ = I/(ma2) mide la relación entre el momento de inercia del aro y la masa de la partícula. Un caso especial es cuando el aro no tiene inercia. El potencial efectivo es entonces
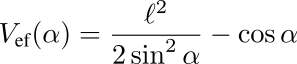
Tiene el aspecto que muestra la figura.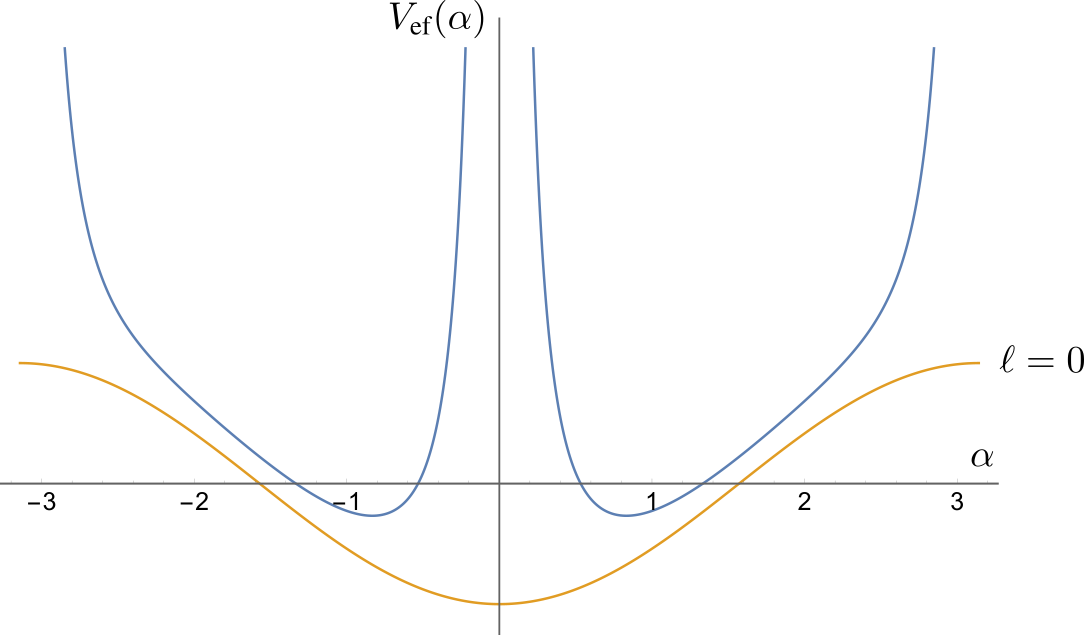
A modo de comparación está graficado el potencial efectivo cuando ℓ = 0. El principal efecto del momento angular son las barreras que impiden cruzar las líneas α = 0, y α igual a ±π, que es en realidad la misma línea.
Aquí viene lo extraño. Cuando ℓ = 0, no hay ninguna barrera, y la partícula hace lo que todos esperamos que haga: oscila como un péndulo, como en la figura de abajo: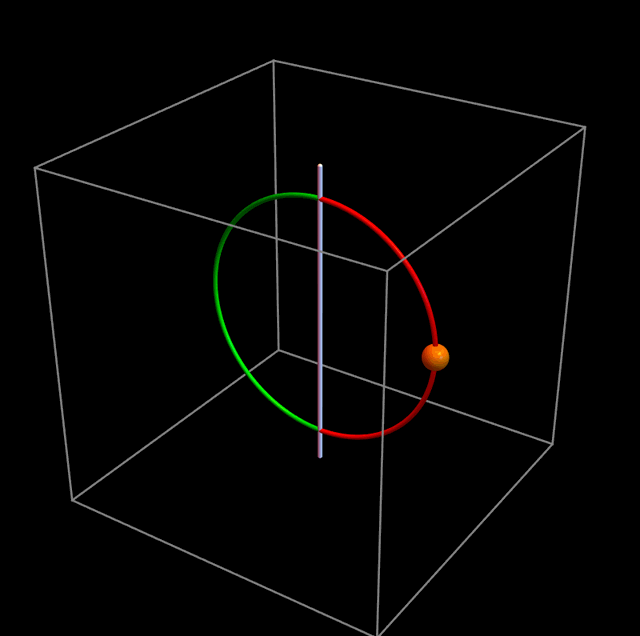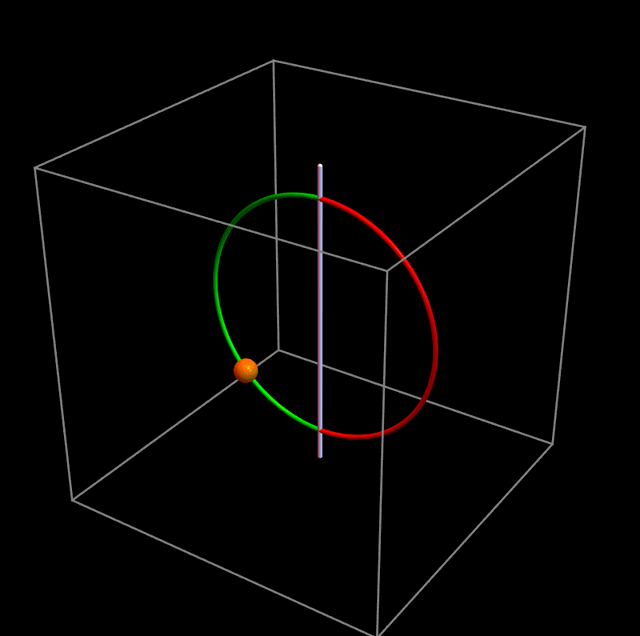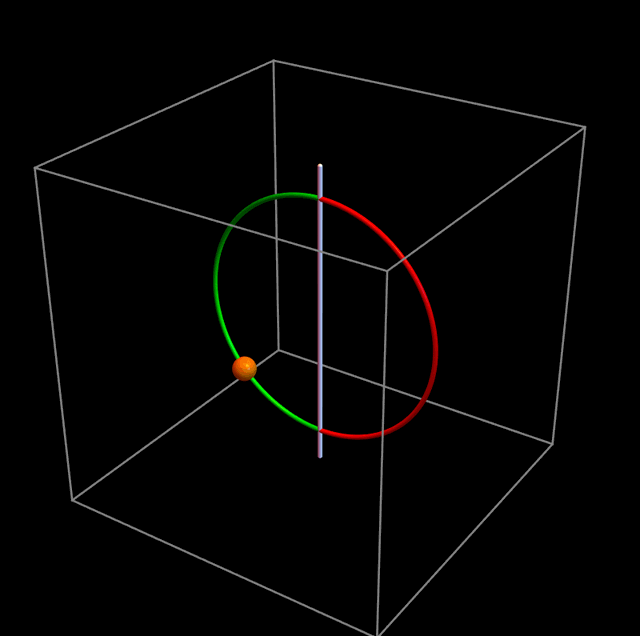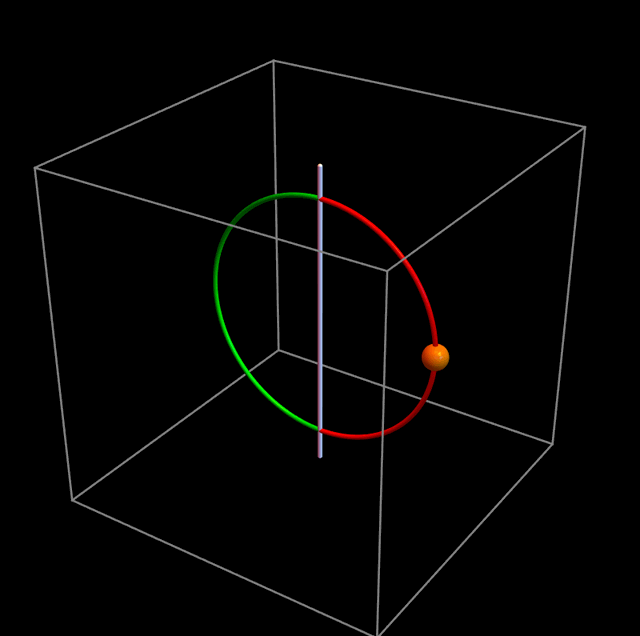
La condición ℓ = 0 es irrealizable en la práctica. Sin llegar a ser nulo, por pequeño que sea ℓ, siempre estarán las barreras de potencial que le impiden a la partícula cruzar de una mitad del aro a la otra. Fíjense que en la animación de arriba la partícula pasa del arco rojo al arco verde sin ningún impedimento. Pero si ℓ no es igual a cero, por mínimo que sea, habrá una barrera de potencial en α = 0. Para ℓ muy pequeño, el potencial efectivo es como en la figura de abajo.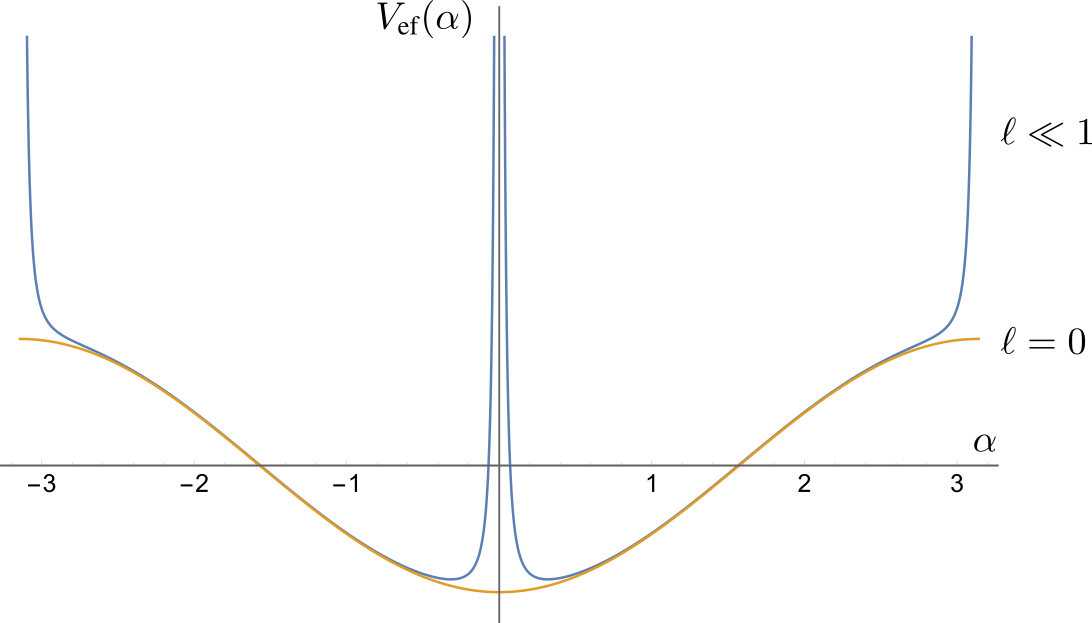
Casi todo el tiempo la partícula sólo ve el potencial gravitatorio. Pero suficientemente cerca del origen está la barrera de potencial que le impide cruzar de un lado al otro del aro. La partícula, aparentemente, debería rebotar como en la figura de abajo:
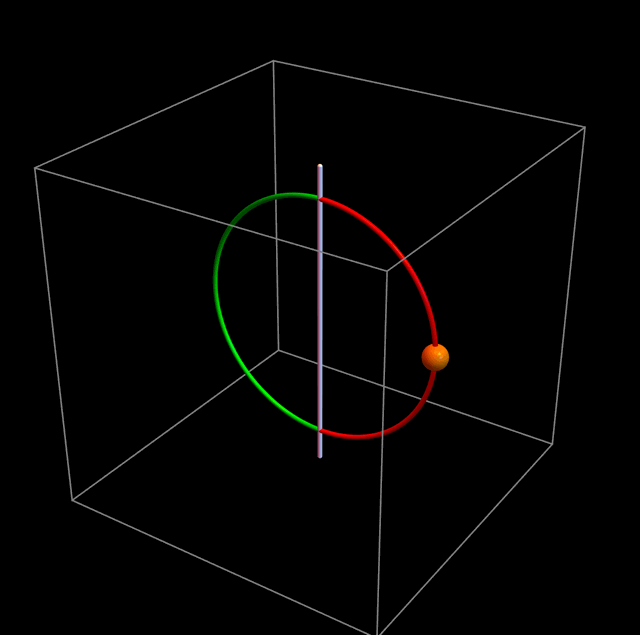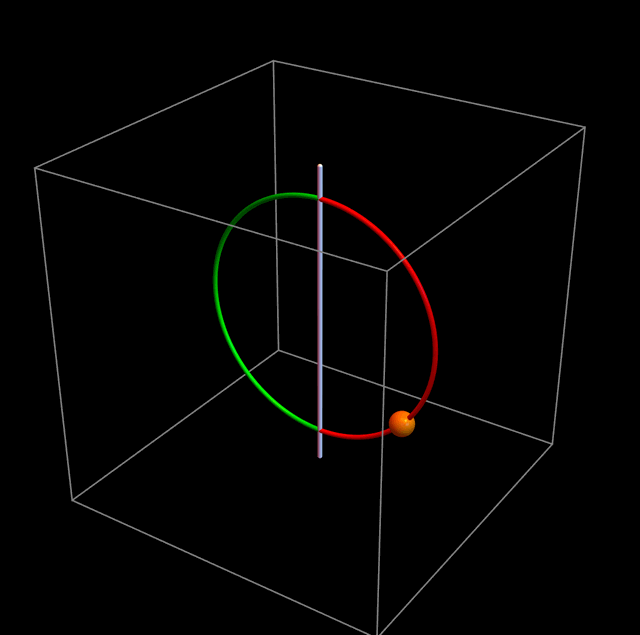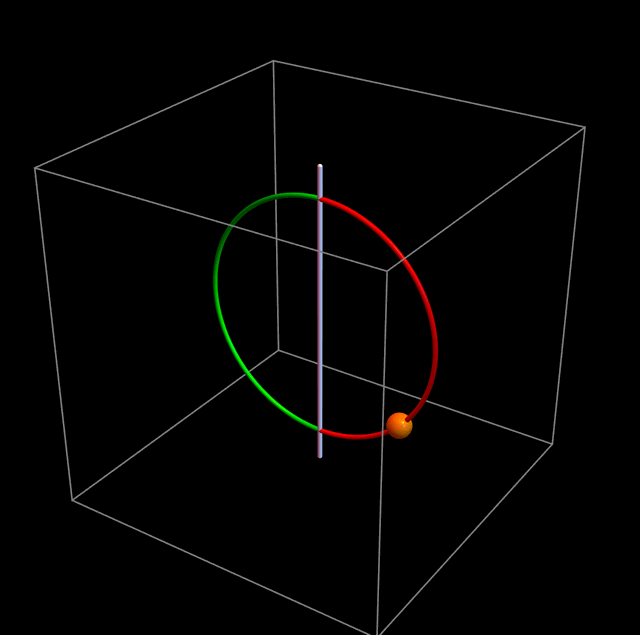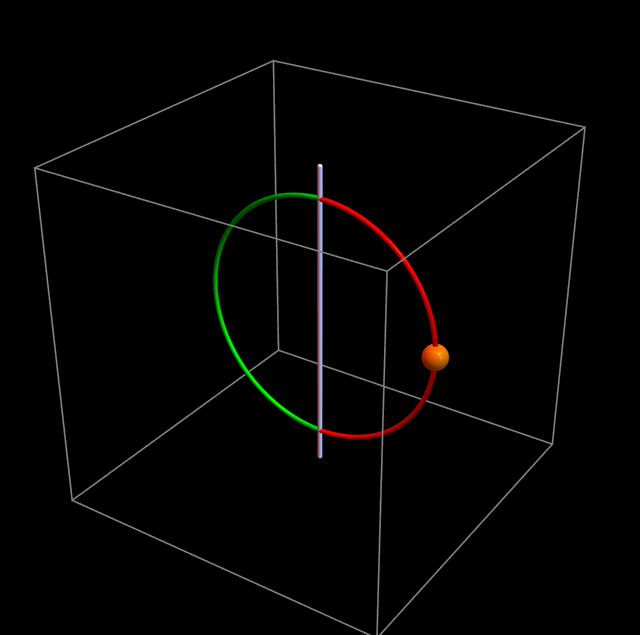
Pero esto es absurdo: situaciones físicamente cercanas tienen que dar lugar a comportamientos físicamente cercanos. Antes de seguir leyendo, deténganse un momento a pensar qué es lo que debería pasar en realidad. Tal vez tengan que escribir alguna ecuación. Voy a insertar una imagen que no viene a cuento para que no caigan en la tentación de ver lo que sigue inmediatamente:
Unos caracteres aleatorios para crear distancia:
Lo que pasa en realidad es lo que muestra la siguiente figura:
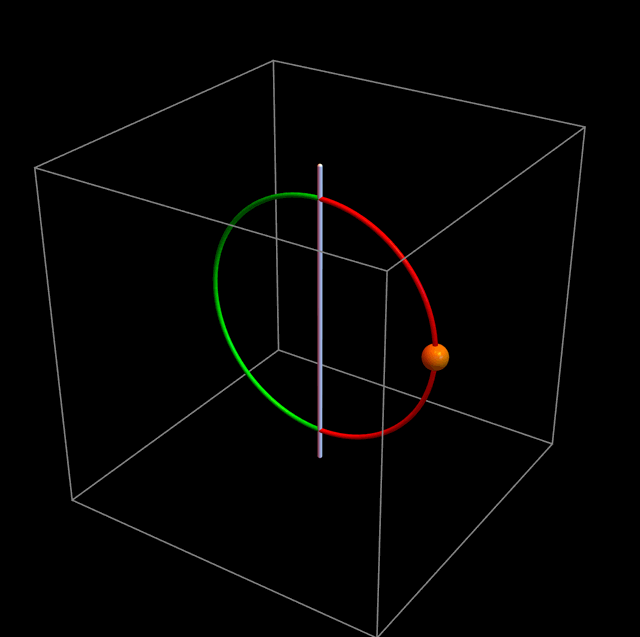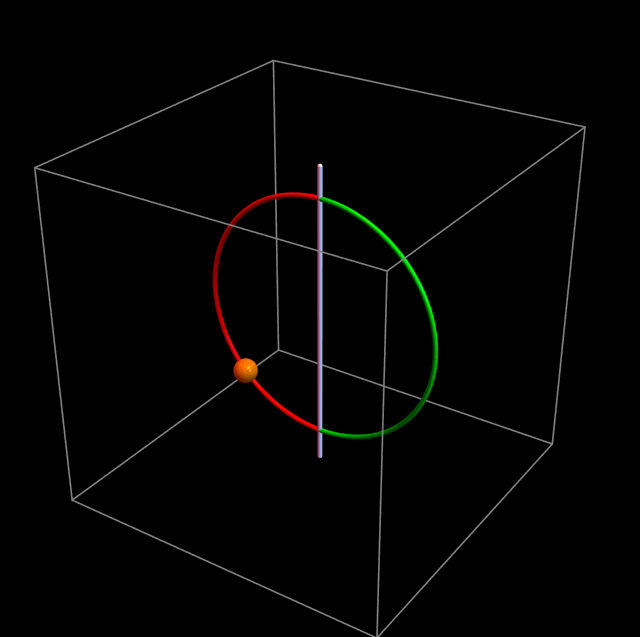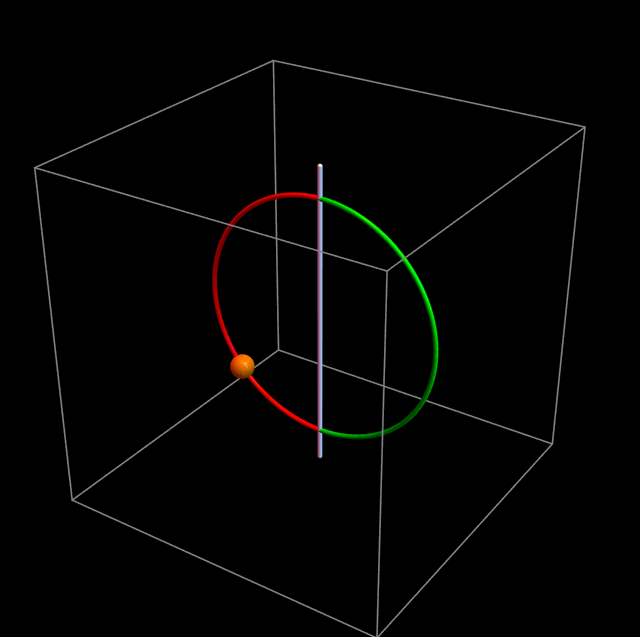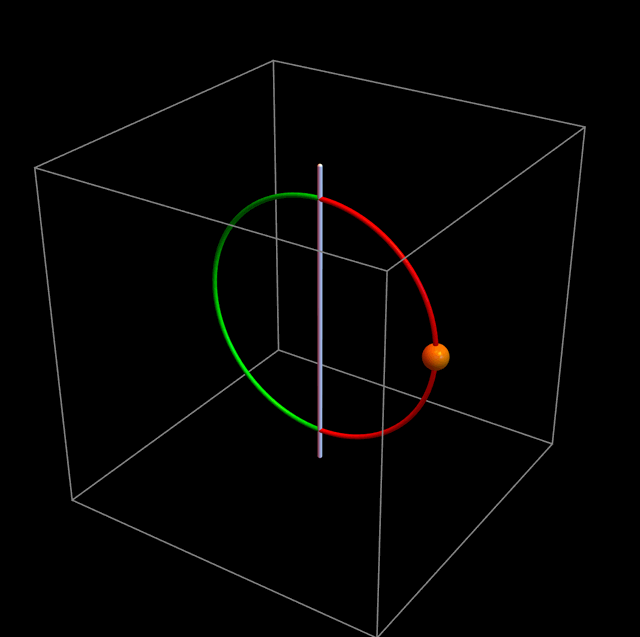
Si no le prestamos atención al aro, la partícula oscila tal como esperaríamos. Noten, sin embargo, que siempre se mantiene en la mitad roja del aro. La partícula verdaderamente está siendo repelida por la barrera de potencial, pero el aro a su vez da súbitamente medio giro, para que la partícula tenga un comportamiento prácticamente indistinguible del caso ℓ = 0. La figura de abajo muestra en cámara lenta lo que ocurre cuando la partícula llega a la barrera de potencial. Noten que el tiempo transcurre a distinta velocidad durante distintas partes de la animación:
El momento angular podrá ser pequeño, pero para ángulos suficientemente pequeños la velocidad de giro del aro puede ser arbitrariamente grande. Recuerden que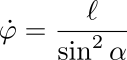
La mayor parte del tiempo, esta velocidad es prácticamente nula, pero cuando el ángulo se aproxima a cero, puede tomar valores tan grandes como se quiera. Es un ejercicio interesante demostrar que para ℓ mucho menor que uno, el aro da justo medio giro cuando la partícula rebota en el punto de retorno.
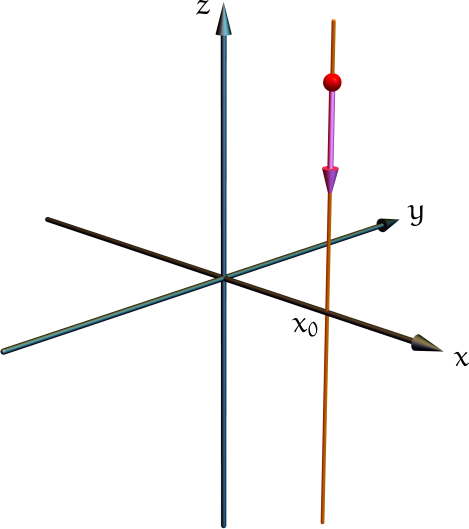
![]() Luego, su momento angular resulta
Luego, su momento angular resulta![]()
![]()
![]()

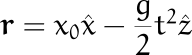
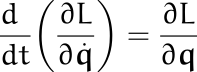
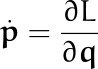 Para el caso específico que estamos analizando, queda
Para el caso específico que estamos analizando, queda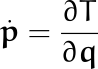
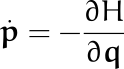
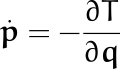 Pero esta ecuación tiene justo el signo contrario de la que escribimos anteriormente
Pero esta ecuación tiene justo el signo contrario de la que escribimos anteriormente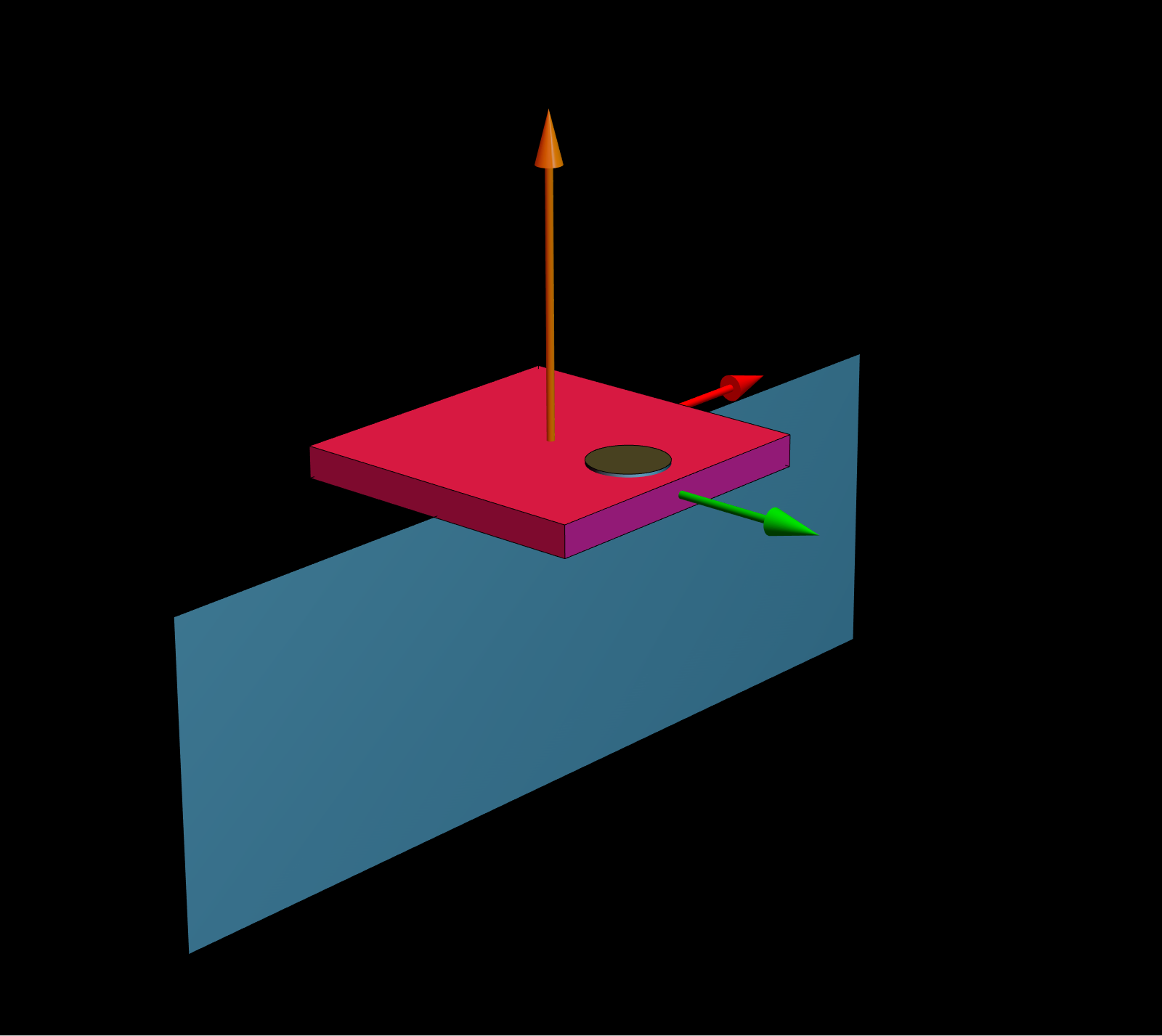 Inicialmente los ejes del cuerpo coinciden con los ejes xyz. Todos los ángulos de Euler son cero. Demostrar que el cuerpo permanece inmóvil.
Inicialmente los ejes del cuerpo coinciden con los ejes xyz. Todos los ángulos de Euler son cero. Demostrar que el cuerpo permanece inmóvil.


 Si siguieron el argumento del problema 13 de la Guía 2, que también pueden
Si siguieron el argumento del problema 13 de la Guía 2, que también pueden