Hola, algunos comentarios varios que me quedaron dando vueltas.

El nivel del segundo parcial estuvo muy bien con muchos aprobados (felicitaciones!). Sin embargo hay dos errores que me gustaría aclarar del ejercicio 1 porque fueron mucho más comunes de lo que esperaba, y no está bueno que se vayan de Meca sin aprenderlos.

El primero es el signo del potencial gravitatorio. Este error parece inocente pero afecta el análisis del Veff. En pequeñas oscilaciones, al cambiar mínimos por máximos las perturbaciones dejan de ser pequeñas! Uno esperaría que despues de F1 y todo Meca ya hubiera quedado claro pero lo repetimos una vez más con la esperanza que lo reflexionen: si F=-∇V , entonces V=-F.r. Si ẑ apunta hacia arriba, F=-mgẑ y V=mgz. Si ẑ apunta hacia abajo, F=mgẑ y V=-mgz.

El segundo fue interpretar un Veff de L (ni hablar de volver a meter cant conservadas en L). El Lagrangiano no es una cantidad conservada para interpretarle un Veff. Aunque L=T-V y uno se ve tentado a decir que L=Teff-Veff, esto último no es cierto.
Si por ejemplo T=m(θ·)²/2+f(ϕ·,θ) y pϕ se conserva, tal que podemos reescribir ϕ· en funcion de pϕ, y además la energia mecánica se conserva, entonces E=T+V=m(θ·)²/2+f(pϕ,θ)+V(θ) y el pot efectivo será Veff(θ)=f(pϕ,θ)+V(θ).
En cambio si definiamos L=Teff-Veff, el Veff(θ)=-f(pϕ,θ)+V(θ)…. hay un signo menos de diferencia que va a romper toda la interpretación!

————————◊————————

Unx de ustedes tenía confusiones sobre las condiciones directas para probar que una transformación es canónica. Como dice la wiki, las ecuaciones de Kamilton se cumplen si valen las siguientes cuatro igualdades:

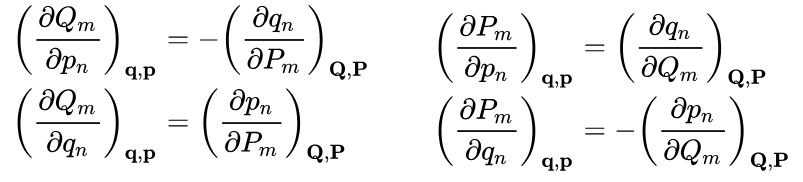Los subíndices indican respecto de que variables hay que derivar.

————————◊————————

Alguien interesadx en aprender a escribir documentos en Latex me pidió la plantilla / el código de los apuntes que subí. Les comparto el tex para que tengan una base. Anímensen!