Buenas, acuerdense que cada tanto vamos subiendo material (simulaciones y apuntes) en la pestaña ‘cronograma de TP’.
Esta vez les dejé unos apuntes con la clase de hoy sobre el ejercicio 7 de pequeñas oscilaciones (3 masas en un aro con resortes). Mirenlón y consulten!

Hola, el lunes alguien olvido una bufanda (tricolor creo, tenia azul y negro). La dejamos en bedelía, busquénla por ahí.
Esto ya pasó un par de veces, asi que revisen bien antes de irse!

Lo mismo para los vasos descartables y etc. Sabemos que no hay un tacho cerca (el porcentaje de gasto en mantenimiento de 1% que mencionaba Berna), pero llevense sus cosas con ustedes cuando se retiran.

Hola,

Les quiero llamar la atención de las simulaciones Vpython que hay en cada Guía. En particular el caso de órbitas elípticas, del problema de Kepler con dos cuerpos. Notar que la masa  mas pesada hace una elipse proporcional al negativo del vector de la masa mas liviana (pues el CM está en el origen). Por eso la elipse que desarrolla no es concéntrica. Esto es diferente al caso de órbitas circulares, donde las trayectorias son círculos concéntricos. La partícula ficticia de masa reducida μ y coordenada relativa r, siempre es concentrica a la trayectoria de la masa más liviana, pues su coordenada relativa posee el signo del vector de posición de la masa liviana.

Ya están posteadas parte de la clase de simetrías generalizadas y de Dispersión (scattering) faltante. No olviden pasar por Cronograma TP.

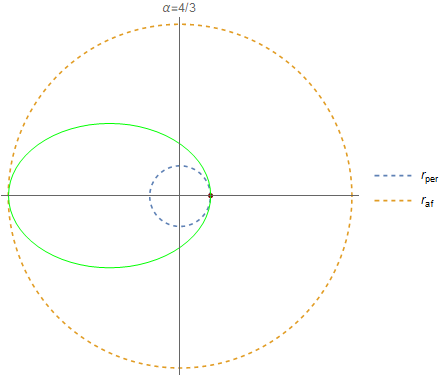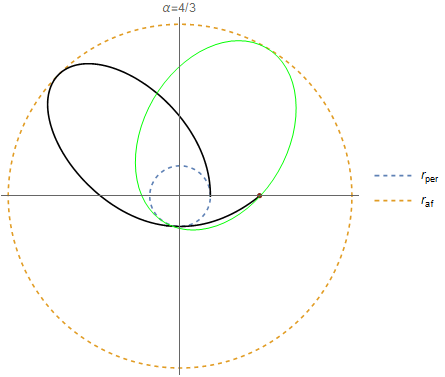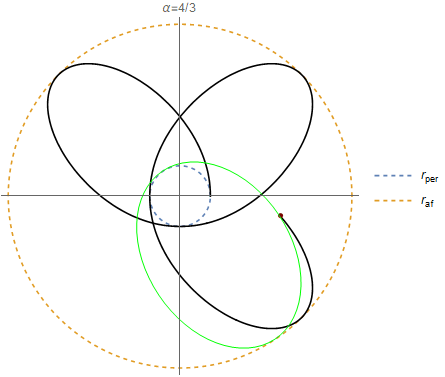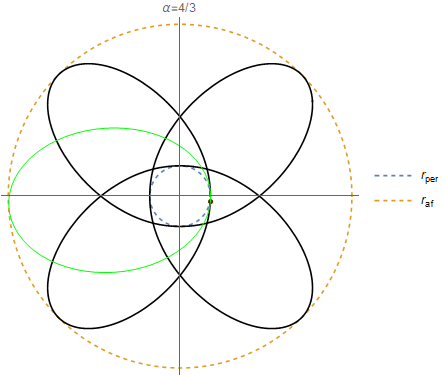
Hola, hoy en clase hablamos de elipses que preceden, como la órbita de mercurio.
En la pestaña de cronograma de TP les deje unas notas con la clase.
Por si la imaginación hoy no les dió para ver la elipse que se movía, acá va un gif clarificador para el caso que vimos α=4/3 :

Si α cambía la trayectoria varía segun las ideas que vimos hoy (recuerden: si α=racional las órbitas son cerradas). Les comparto un gif hipnótico variando α, graficando hasta φ=6π.

–––––––––◊–––––––––

Extra: Tabla de Integrales

En el ejercicio 4 les pide hallar la trayectoria, para lo cual deben hacer una integral. La solución de esa integral, similar a la que hay que hacer en Kepler y oscilador armónico, depende mucho de los signos de los parámetros. En (3.51), Goldstein nos da, tímidamente, una sola solución. Buscando un libro de tablas de integrales, encontramos la que buscamos en la 2.261. Si R=a+bx+cx² y Δ=4ac-b

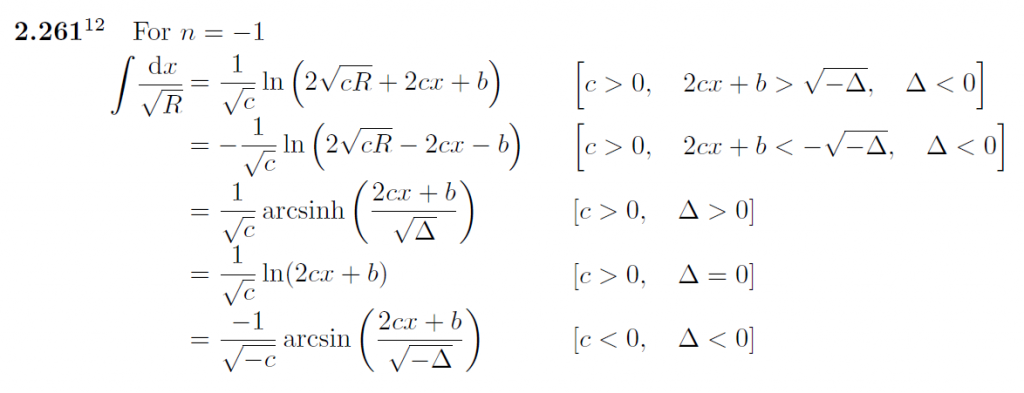Espeluznante! Les prometo que si toman φ0=0 en el punto de retorno r0 (E=Veff|ᵣ₌ᵣₒ), las soluciones se simplifican bastante.
De paso es bueno recordar que los logaritmos se relacionan con funciones hiperbolicas inversas, ver la wiki.