Teaser (para ver en pantalla completa):

Se ha escrito que

al estudiar [el formalismo de las transformaciones] canónicas, es tentador renunciar desde el principio a todo intento de visualización. Se da por hecho que las variables canónicas son meros símbolos intraducibles, con los que hay que lidiar sin comprender realmente su significado. Eso tal vez sea cierto en muchos casos, pero sin duda no lo es para las variables de ángulo-acción.

Y es una notable falta que en los libros  se omita decir que las variables de ángulo-acción no son más difíciles de entender que las coordenadas polares en el plano. Las transformaciones canónicas permiten cambios de variables tan extraños que es comprensible no entender qué significan, por ejemplo, las nuevas coordenadas Q = Log[sin p/q] y P = q ctg p. Pero esto no es excusa en el caso de las variables de ángulo-acción.

En este [archivo] nos dedicamos a mostrar lo dicho más arriba, usando dos ejemplos de potenciales sencillos, pero con variables de ángulo-acción con una geometría muy interesante de ver. Lo que sigue aquí es un resumen.

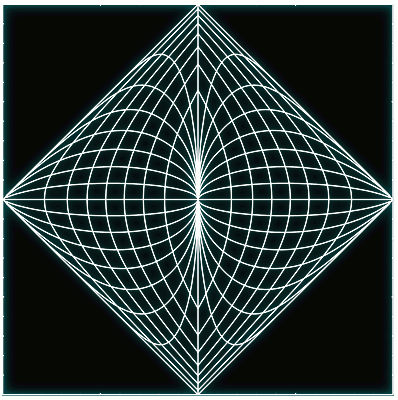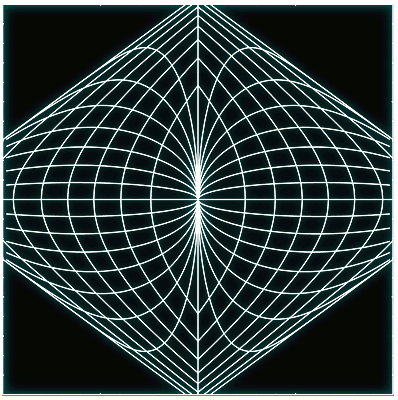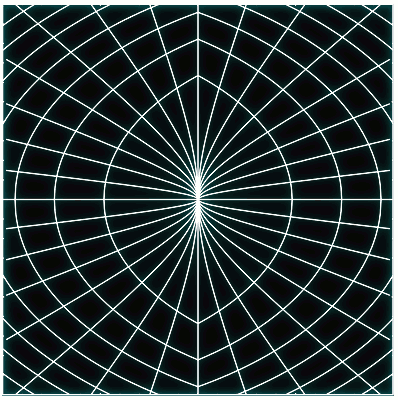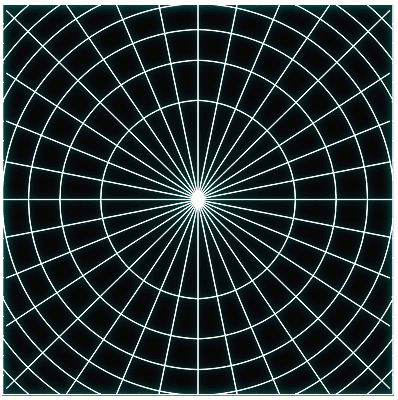
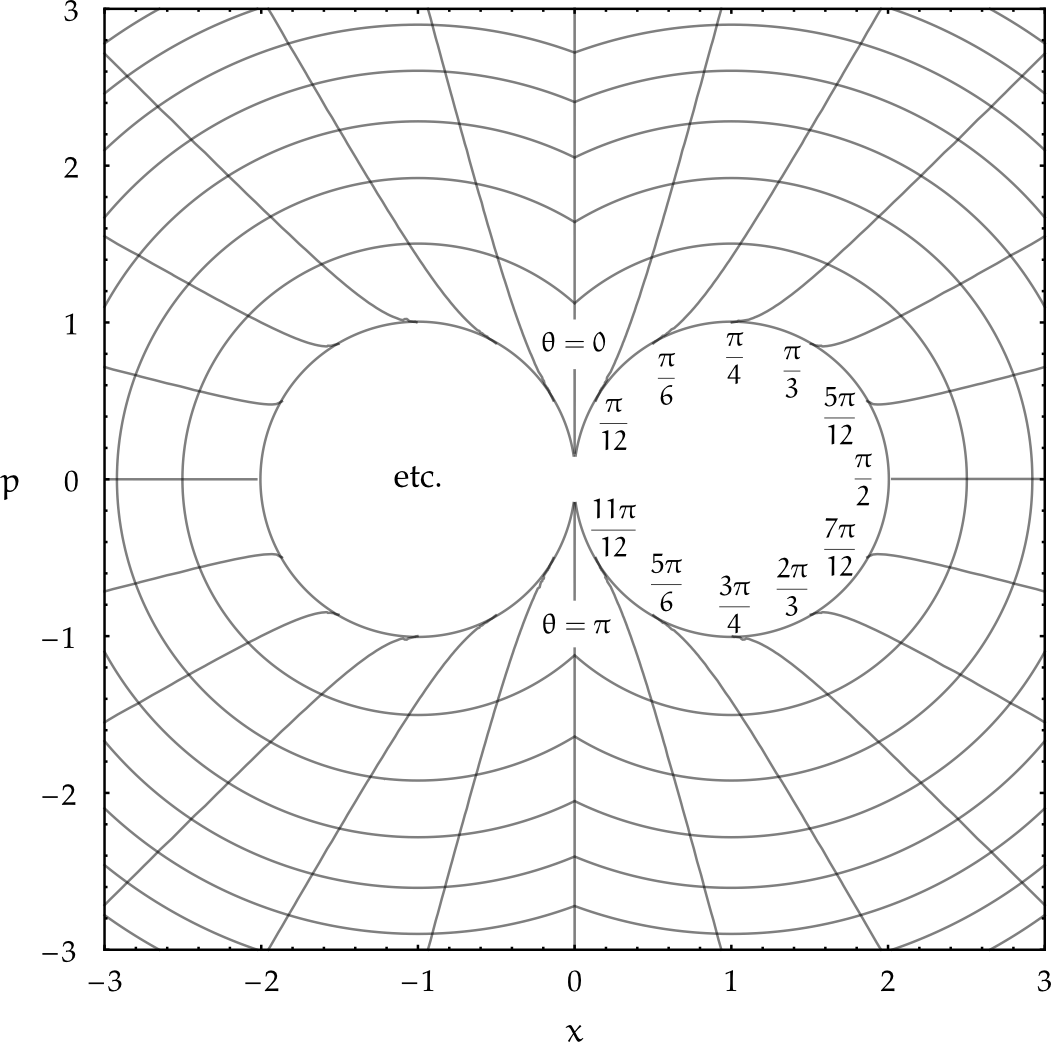
 Uno de los potenciales analizados es el pozo doble del problema 24 de la Guía 7, cuyas variables de ángulo-acción generan las siguientes curvas coordenadas en el plano (x,p).

Este cambio de coordenadas es válido en la región del espacio de fases en donde la partícula orbita alrededor de los dos mínimos del potencial, como un perro alrededor de dos estrellas, cuya felicidad cantan los poetas.

El otro ejemplo considera un potencial parametrizado de tal manera que permite estudiar toda una familia de transformaciones de ángulo-acción. El rango de formas y colores que toma el potencial, junto con su retrato de fases, pueden verse en la siguiente animación.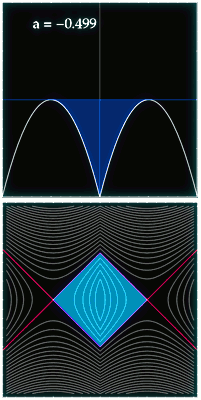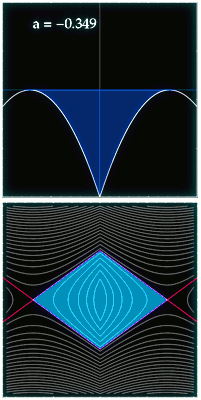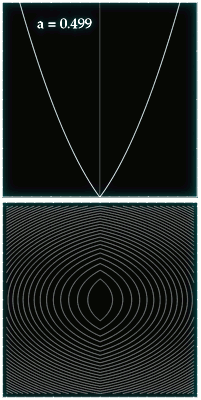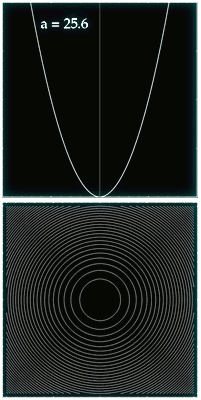Si han leído todo lo anterior, entonces no tendrán que esperar a que se cargue la animación de abajo, que muestra la evolución de las coordenadas de ángulo-acción a medida que se varía el potencial. Más detalles en el pdf.