Cuando el potencial que aparece en el lagrangiano gira con velocidad angular constante, hay una cantidad que se conserva, J = ε - ω L, donde ε es la energía, ω la velocidad angular del potencial y L la componente del momento angular en la dirección de ω. Por ejemplo, despreciando la influencia de la Luna y de los otros planetas, el movimiento de un satélite puede pensarse como el de una partícula atrapada en el potencial gravitatorio que producen la Tierra y el Sol, y que, por lo tanto, rota con una velocidad angular aproximadamente constante, con una frecuencia de 1 ciclo/año.
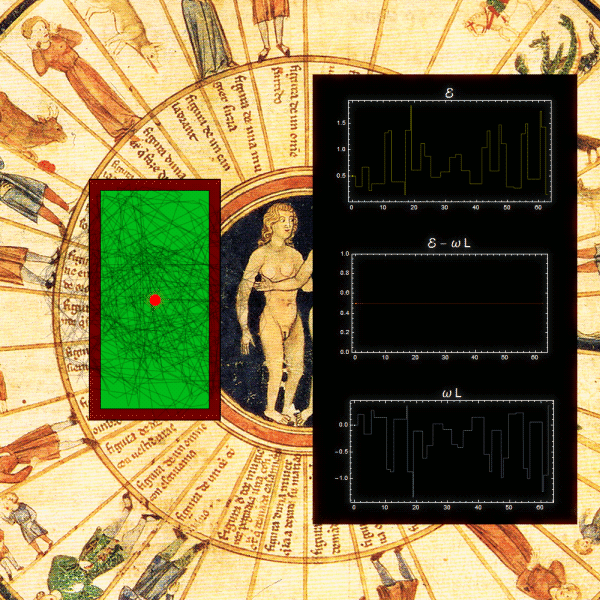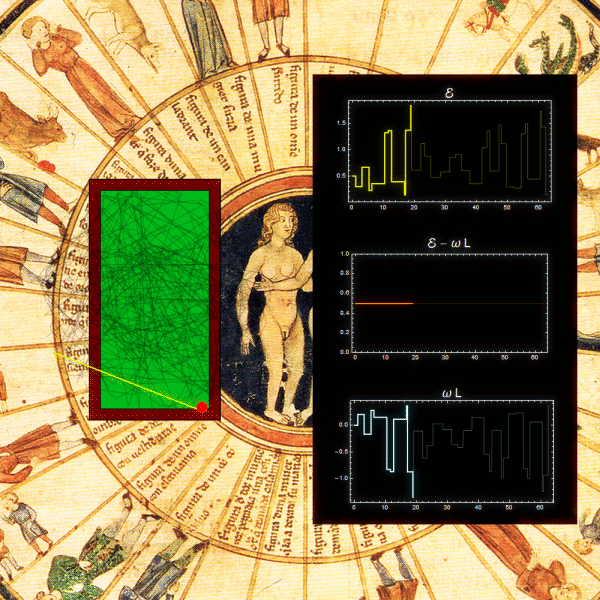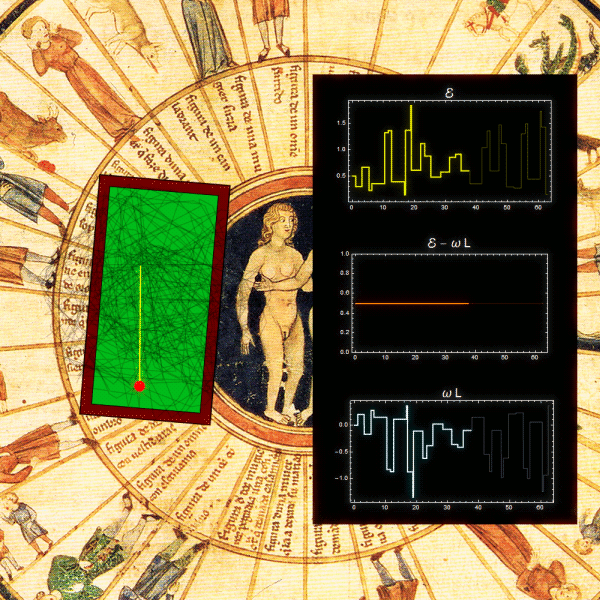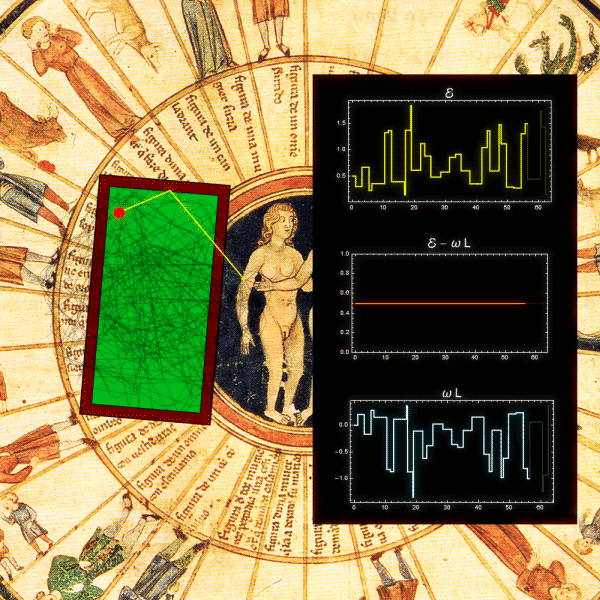
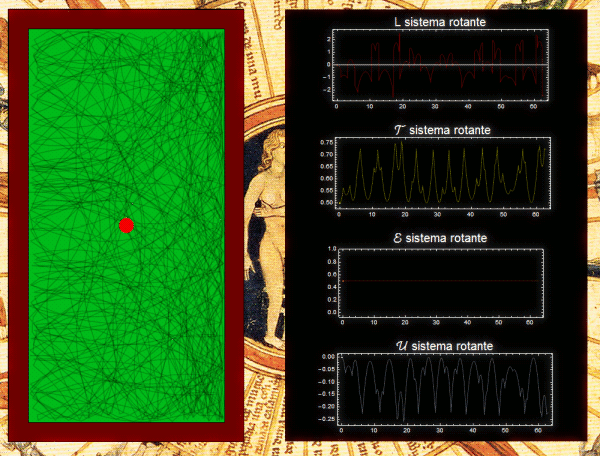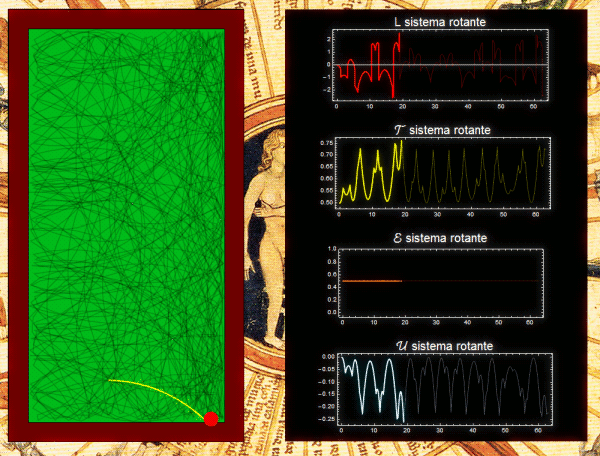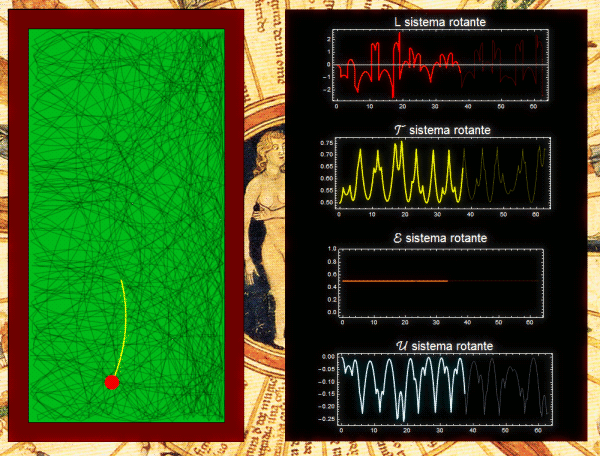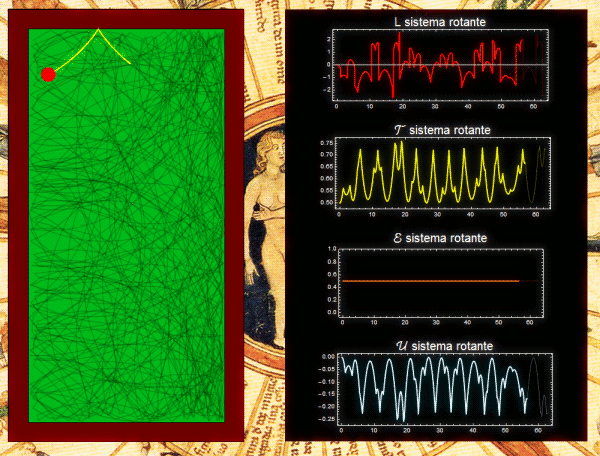
Una mesa de billar giratoria es otro ejemplo. La condición de que la o las partículas estén confinadas a moverse dentro de la mesa, puede garantizarse asumiendo que hay un pozo de potencial suficientemente profundo. Sin importar la forma de la mesa, ni lo complicadas que sean las trayectorias, J se conserva. La animación de abajo corresponde a una mesa rectangular (link en la imagen: video ampliado).
Si el lagrangiano se escribe en términos de las coordenadas de un sistema no inercial fijo a la mesa, en ese sistema el potencial es independiente del tiempo, y por lo tanto se conserva h. Ahora bien, en este sistema además del potencial original hay también potenciales asociados a la fuerza centrífuga y a la fuerza de Coriolis (aunque en realidad esta última fuerza no realiza trabajo). Lo que puede verse es que la cantidad conservada es igual a la energía cinética (calculada en el sistema no inercial), más la energía potencial centrífuga más la energía potencial original. La siguiente animación muestra la misma trayectoria de antes pero representada en el sistema fijo a la mesa. Las cantidades graficadas a la derecha están referidas a este sistema. En el fondo de la figura se ve rotar el sistema inercial, en sentido contrario al sentido de rotación de la mesa en la figura anterior (link en la imagen: video ampliado).
Aquí abajo, la comparación lado a lado de las dos descripciones.
Y un par de papers, [aquí] + un excelente paper que subieron a la página de MC(A). Encontrarán demostraciones del Teorema de Noether, aplicaciones al caso particular de potenciales que giran, y miles de otras cosas.