Por la reunión de la AFA esta semana tuvimos clase teórica solo el lunes, considerando especialmente que el tema que empezamos a tratar (descomposición empírica de datos) puede ser especialmente útil para estudiantes de doctorado.
Para los que no estuvieron en la clase del lunes, acá pueden encontrar los breves apuntes de los temas que vimos en esa clase:
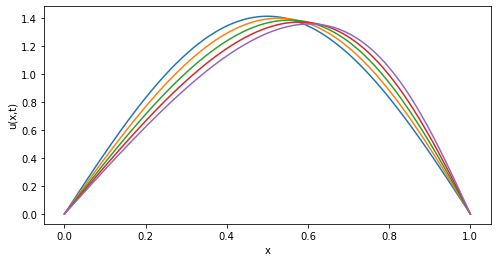
En la clase también mostré un Colab comparando el resultado de integrar la ecuación de Burgers, y el sistema de ecuaciones ordinarias resultantes de hacer la truncación de Galerkin truncando a solo 3 modos. No dejo el Colab acá ya que para las guías de ejercicios tendrán que hacer algo parecido. Pero les dejo los resultados. Si uno integra la ecuación de Burgers en el recinto [0,1] con condiciones de contorno
u(0,t) = u(1,t) = 0,
con condición inicial
u(x,t) = √2 sin(πx),
y con viscosidad ν = 0.05, esto es lo que se obtiene para u(x,t) en diferentes tiempos (azul corresponde a t = 0, seguido por naranja, verde, rojo y violeta):
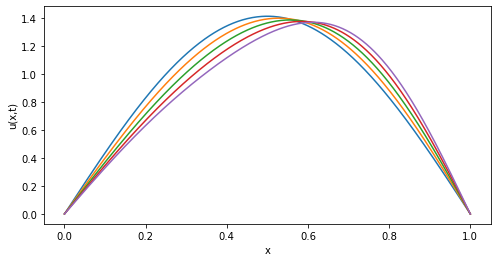
Por otro lado, si uno integra el sistema de ecuaciones ordinarias que está en el apunte (con 3 modos, es decir, para los coeficientes a1, a2 y a3), la evolución del sistema puede reconstruirse usando
u(x,t) = √2 [ a1(t) sin(πx) + a2(t) sin(2πx) + a3(t) sin(3πx) ]
El resultado de integrar las ecuaciones ordinarias y reconstruir u(x,t) se muestra en la siguiente figura:
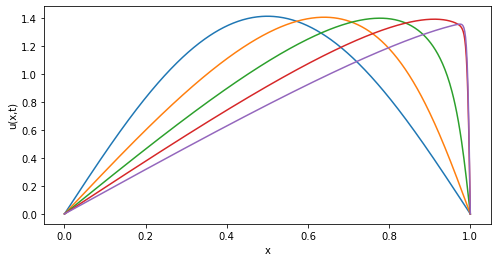
Noten que el sistema reducido captura la misma dinámica que el sistema completo (¡dado por la ecuación en derivadas parciales!). Pero esto deja de valer si la viscosidad es muy pequeña, porque se necesitan mucho más que 3 modos para describir correctamente la dinámica. Por ejemplo, para ν = 0.005 la evolución con la ecuación de Burgers es
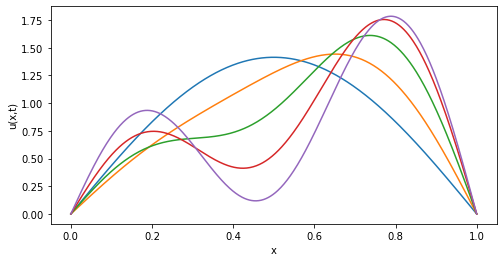
Mientras que la integración del sistema truncado de ecuaciones ordinarias, para la misma viscosidad y los mismos tiempos, da algo muy diferente: