Para aquellos que asisten a la reunión de la AFA, esta semana haré un breve resumen de las clases en la página de la materia. El lunes vimos la ecuación de Kardar-Parisi-Zhang (KPZ), una ecuación estocástica que describe el crecimiento de superficies. Las ecuación KPZ puede transformarse en la ecuación de Burgers. A lo largo de la clase también vimos cómo usar la transformación de Hopf para encontrar soluciones exactas a estas ecuaciones, y también como buscar soluciones de ondas viajeras para estos sistemas.
Estos son los apuntes de la clase:
En la clase también mostré un Colab que integra la ecuación KPZ en el recinto [0,2π) con condiciones de contorno periódicas, y con un forzado aleatorio con valor medio nulo y delta-correlacionado en el tiempo, a partir de una condición inicial u(x,0)=0 (es decir, una superficie sin deformación). La evolución temporal de u(x,t) para diferentes tiempos es la siguiente (en la figura cada tiempo está desplazado verticalmente):
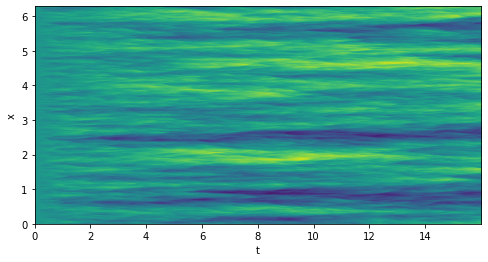
Noten como la superficie crece en el tiempo en forma desordenada, creando picos y valles. La ecuación KPZ describe el crecimiento de superficies por deposición balística (como ocurre en sedimentación), el crecimiento de superficies de óxido, y otros procesos de crecimiento de superficies. En un diagrama espacio-temporal, la evolución de u(x,t) se ve de la siguiente forma (amarillo corresponde a picos, y azul a valles):
Una propiedad interesante de esta ecuación es que sus soluciones son fractales: al hacer zoom en la superficie, un obtiene una nueva superficie que estadísticamente indistinguible de la superficie previa. En otras palabras, las soluciones son auto-semejantes. La siguiente figura ilustra esto mostrando una solución a tiempo fijo, u(x,t), y dos zooms sucesivos (en 1/2 y 1/4 del recinto). Noten lo parecidas que son las soluciones: