Hola, les aviso que hoy Jueves 16/05 va a haber clase tanto teórica como práctica como es ususal.
Nos vemos,
Federico

Hola, les aviso que hoy Jueves 16/05 va a haber clase tanto teórica como práctica como es ususal.
Nos vemos,
Federico
Hola, les aviso que el parcial es a las 17 en el aula de la cursada (Aula 4 – Pabellón 2).
Nos vemos,
Federico
Hola, les aviso que recién subí los apuntes de los temas que vimos el Martes sobre momento angular.
Les recuerdo que el Lunes estaremos dando consultas adicionales (ver el post anterior por los horarios).
Finalmente, les aviso todes que, como dije la última clase, no traigan hojas de fórmulas, todas la fórmulas que necesiten van a estar escritas en el parcial (por ejemplo las definiciones de los a y a^\dagger, las fórmulas de Baker-Campbell-Hausdorff y similares, definiciones de J+ y J- y el factor que sacan multiplicando cuando operan sobre el |jm>, etc.).
Nos vemos,
Federico
Hola, les aviso a todes que el Viernes y el Lunes vamos a poner horarios adicionales de consulta.
Viernes: de 14 a 17 en el bar del pabellón 1 vamos a estar Guille y yo (Federico).
Lunes: de 14 a 16 en el bar del pabellón 1 vamos a estar Joaquín y yo y de 17 a 19 Lau y yo.
Nos vemos,
Federico
Hola, en el links de los apuntes, subí una versión actualizada de los apuntes sobre oscilador armónico, donde fundamentalmente agregué la resolución del problema 9 del Oscilador Forzado que comenté al final de la clase pasada (además de agregué algunas cosas en la parte de evolución temporal de estados coherentes y del operador de desplazamiento).
Aprovecho para hacerles algunos comentarios sobre estados coherentes, en particular sobre la generación y medición experimental de estados coherentes que no llegué a contarles en clase. Para aprovechar algunos de los comentarios, les sugiero resolver / darle una leída al problema 9 del oscilador forzado.
El primer sistema sobre el que les quería contar es el de iones atrapados (trapped ions). En estos sistemas se genera un campo eléctrico que tiene un mínimo en una dada posición del espacio. Luego, se bombardea la región donde está el campo con átomos ionizados (por ejemplo Berilio, Calcio, Ytterbio, etc, dependiendo de cada sistema particular). Cuando un ion justo pasa por el mínimo del campo, quedará allí atrapado. Si además se puede garantizar que el ion nunca se aparta significativamente del mínimo (esto se logra enfriando al ion con apropiadas técnicas), entonces de forma análoga a como se hace en mecánica clásica, el potencial se puede aproximar por una parábola, es decir un potencial armónico y tendremos que el ion se comporta como un oscilador armónico cuántico. Acá pueden ver una foto de un único ion atrapado (la mancha entre las dos puntas) [Foto por David Nadlinger, University of Oxford].

Y acá pueden ver la medición de 7 iones atrapados oscilando en un modo normal [mediciones producidas por Ferdinand Schmidt-Kaler en el grupo de Rainer Blatt, Quantum Optics and Spectroscopy, Universität Innsbruck].

Mediante distintas técnicas, que exceden lo que se puede explicar por ahora sencillamente con lo que conocen, el ion se puede preparar en los distintos estados |n〉y se puede medir proyectivamente sobre esta base. Para generar estados coherentes, en este paper del 1997 del grupo de Wineland (Leibfried, D., et al. Journal of Modern Optics 44.11-12), se utilizó justamente el método estudiado en el problema 9 del oscilador forzado: se encendió un forzado mediante otro campo eléctrico y se llevó el sistema al estado fundamental de este nuevo Hamiltoniano que, como demostraron en el ejercicio, es un estado coherente. La única diferencia es que en el experimento mencionado el forzado es dependiente del tiempo mientras que el caso sencillo estudiado en el problema 9 es independiente del tiempo. En este caso más general la solución analítica también se puede obtener (pueden ver este problema resuelto en las notas del curso de Juan Pablo Paz que están en el material adicional). Cualitativamente el resultado es el mismo salvo que permite mayor flexibilidad porque en el caso dependiente del tiempo, variando durante cuánto tiempo está prendido el forzado permite elegir cuál es el estado coherente del sistema, mientras que en nuestro caso el estado coherente no se puede variar.
Acá les adjunto la figura 4 del paper mencionado:
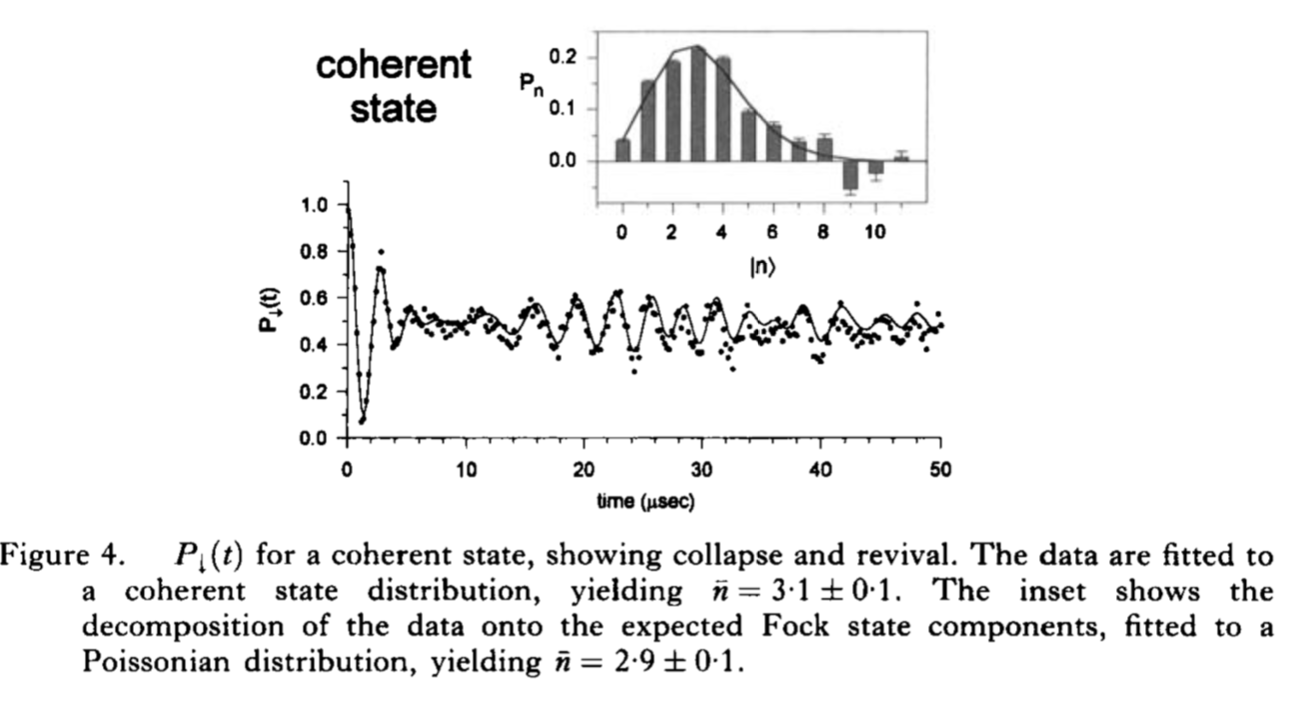
En el gráfico de barras se muestra la distribución P(n) y un ajuste por una distribución de Poisson. Recordemos una cuenta que hicimos en clase. Un estado coherente es de la forma
y por lo tanto la distribución de probabilidad de medir un estado |n〉es
que no es más que una distribución de Poisson con valor medio el módulo cuadrado de α. Vemos efectivamente que en el experimento miden la distribución esperada (nota sobre el paper: cuando dice base de Fock se refiere a la base |n〉, en cuanto a la oscilación que se muestra en el gráfico, es la medición que se usa para inferir P(n), pero los detalles van más allá de lo que se puede contar con lo que vimos, lo importante es que les permite inferir P(n)).
Cabe notar que, como mencionamos alguna vez en clase, medir una distribución de probabilidades de un observable, en este caso P(n), no es suficiente para determinar cuál es el estado cuántico (pues no hay información sobre las fases relativas). Por lo tanto, esa medición por si sola no es suficiente para asegurar completamente que el estado es un estado coherente.
Para poder asegurar que el estado es efectivamente un estado coherente, es necesario hacer algo un poco más sofisticado, como hacen por ejemplo en este paper (Kienzler D., et al. Science: 1261033) del 2014, donde además de poder medir proyectivamente sobre la base |n〉, pueden también medir sobre una base que se obtiene aplicando un desplazamiento D(α) sobre todos los elementos de la base, es decir sobre la base
(que es análoga a la base que se define en el problema 9 para el caso particular del α calculado en el ítem (d)). Como las operaciones unitarias preservan ortonormalidad, entonces si tenemos un estado coherente |α〉y medimos en la base |n, α〉entonces
Por lo tanto, en la nueva base sólo se debería obtener el resultado n = 0. En el paper de Kienzler, et.al. mencionado, justamente hacen esto y se obtienen los resultados que adjunto en la figura
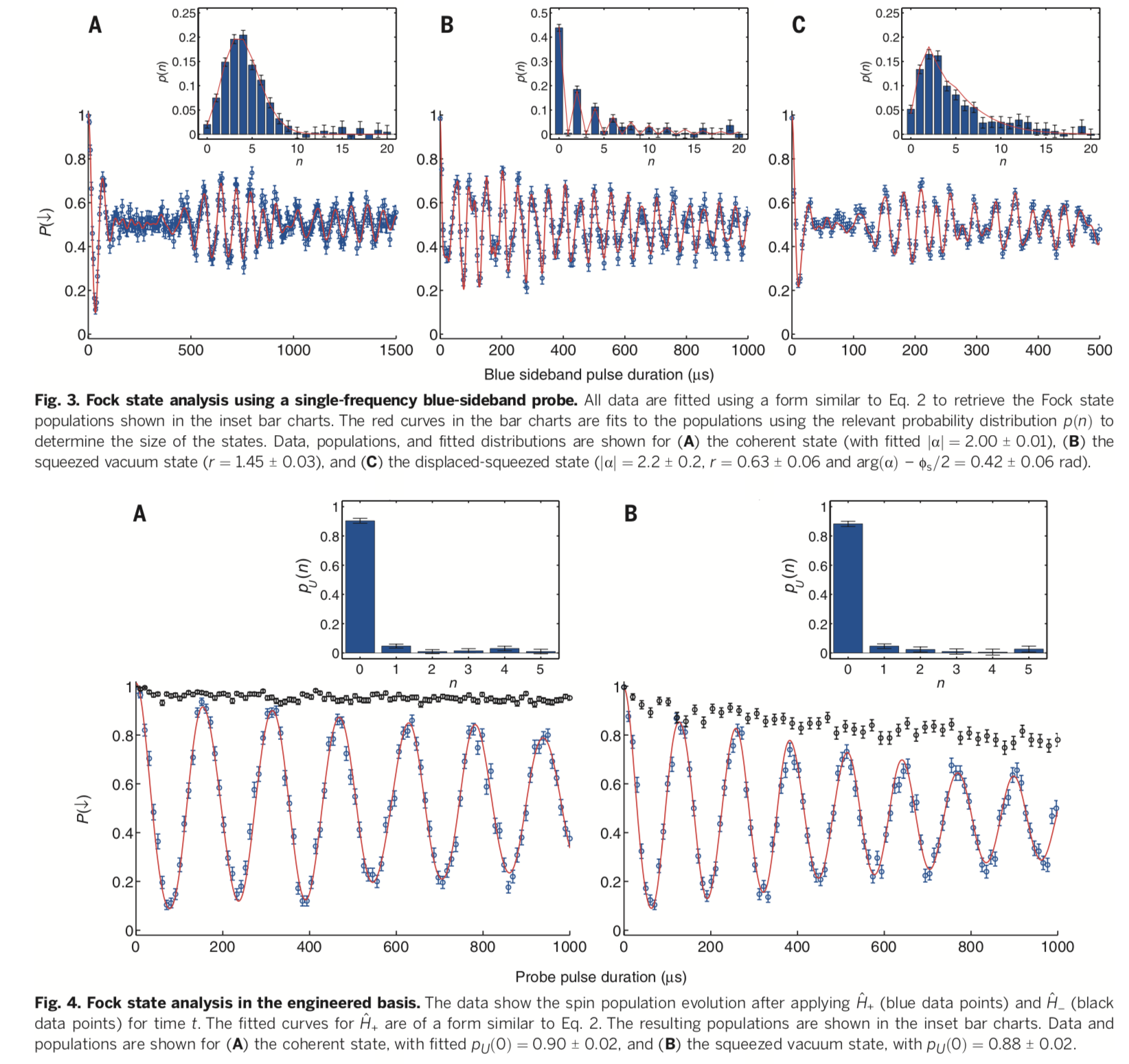
En la figura 3-A se muestra el mismo gráfico del paper anterior: la medición de P(n) y el ajuste por una distribución de Poisson. En la figura 4-A se muestra el resultado de la medición en la base trasladada; se observa que efectivamente solamente se tiene una probabilidad apreciable de medir n = 0, lo cual confirma que efectivamente tienen un estado coherente con el α correspondiente al de la base corrida en que midieron.
Cabe destacar dos cosas: primero, en el primer paper también logran determinar que el estado es un estado coherente porque logran medir todos los coeficientes del estado, tanto probabilidades como fases relativas; esto está contado al final y está hecho con una técnica parecida a la que les mencioné en el segundo experimento, pero así como está contando y reportado (en términos de matrices densidad, que es algo que vamos a ver más adelante en la materia), quizás no es tan claro con lo que saben por ahora cómo lo hacían, mientras que en el segundo caso se muestra explícitamente la medición sobre una base que es muy parecida a la que se ve en el problema 9. Por último quería notar que en el segundo experimento el método de generación de estados coherentes es diferente al del caso anterior y al estudiado en el problema del oscilador forzado.
Finalmente, les quería contar un último ejemplo de medición de estados coherentes, que es para el caso del campo electromagnético. Esto es algo que no vemos en la materia, pero les mencioné la clase pasada; si uno escribe el Hamiltoniano del campo electromagnético libre de fuentes y usa las ecuaciones de Maxwell pero promoviendo ahora todos los campos a operadores, eventualmente se puede demostrar que el resultado es que el Hamiltoniano se puede escribir como una suma de distintos osciladores armónicos cuánticos a distintas frecuencias ω, correspondientes a la distintas posibles frecuencias del campo electromagnético. En este contexto, como les mencioné en clase, el autovalor n del operador de número es literalmente el número de fotones en el campo. Si me creen esto sobre el campo electromagnético, entonces les puedo mostrar este resultado muy lindo obtenido por Breitenbach, et. al. en 1997, en este paper, del cual adjunto parte de la figura 2
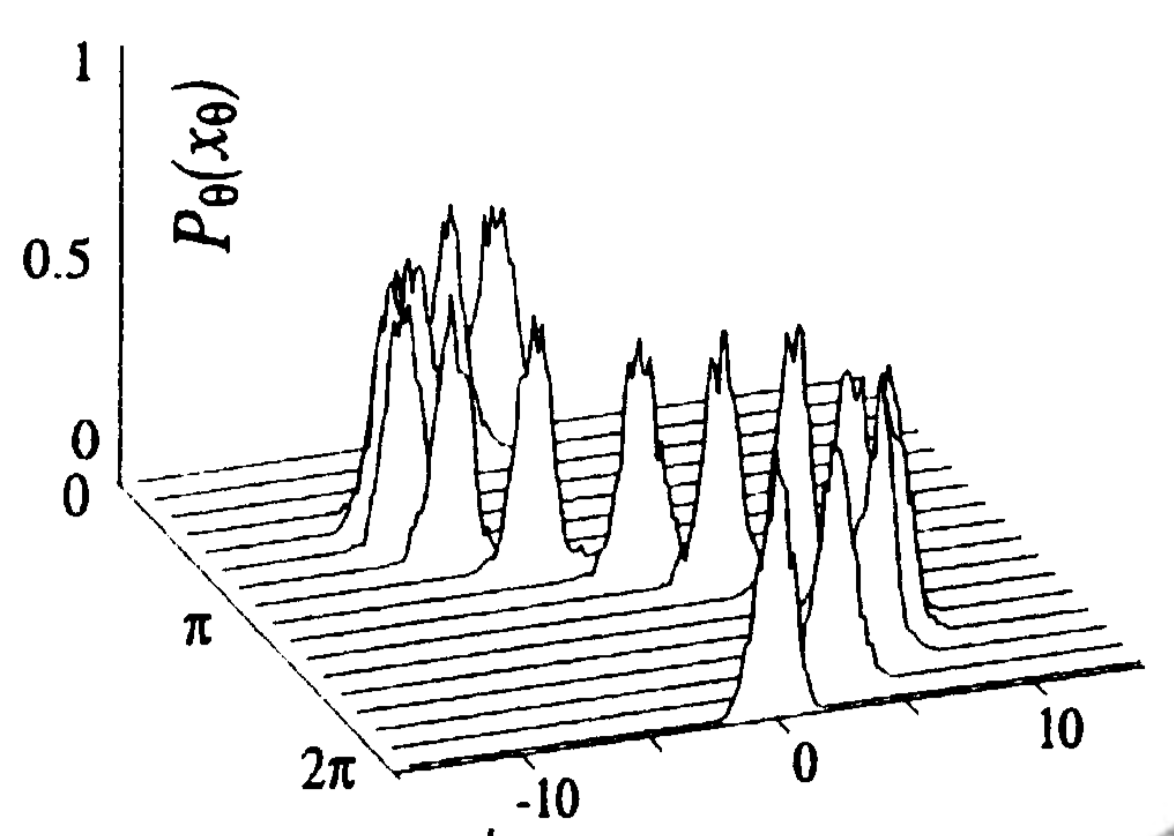
donde se grafica la densidad de probabilidad medida experimentalmente en función de la posición (eje en el plano de la pantalla) y en función del tiempo (eje que entra dentro de la pantalla). Vemos que efectivamente se ven las oscilaciones armónicas del centro de la gaussiana en función del tiempo como calculamos en clase para un estado coherente. En este paper hacen además una medición de todos los coeficientes del estado del sistema (probabilidades y fases) y verifican que efectivamente es un estado coherente (esto está reportado al final, aunque en el lenguaje de matrices densidad, que veremos más adelante en la materia).
Espero les haya parecido interesante y por supuesto están invitados a mirar los papers, aunque va haber muchas cosas que no entienden (pero seguro van entender más de si hubiesen agarrado esos papers antes de empezar la cursada!) y también están invitados a hacer cualquier pregunta.
Nos vemos,
Federico
Hola, en el mismo link de antes subí también unos apuntes de la guía de Oscilador Armónico.
Les aviso que además actualicé el de dinámica: le agregué algunas cosas y corregí un error de tipeo en una ecuación del problema 2.
Nos vemos,
Federico
Hola, acá pueden encontrar una versión digital de unos apuntes míos de la guía de Dinámica. Quizás les pueden resultar útiles. Están resueltos los problemas que resolvimos en clase más el problema 4 del guía 4 (que no vimos en clase). Este último ejercicio, aún si ya lo resolvieron, quizás les puede resultar útil mirarlo, dado que varias de las preguntas están resueltas de más de una forma.
Salvo que lo quieran imprimir, les sugiero mirar el apunte desde el link, porque como ahí está en mi drive, si lo actualizo para agrega/corregir cosas ven los cambios inmediatamente.
Por las dudas, si no vieron el post de ayer, les recuerdo que por el motivo del paro la clase de hoy está suspendida.
Nos vemos,
Federico
Hola, en vista de que por el paro del Martes 30/04:
decidimos suspender tanto la clase práctica como teórica.
En cuanto a la práctica, el parcial se mantiene en princpio para la fecha originalmente estipulada. Para compensar la clase menos, de la guía de momento angular veremos solamente la primer parte, quedando la segunda para el segundo parcial (después les confirmo exactamente hasta qué ejercicio de la guía de momento angular).
Nos vemos,
Federico
Hola, me acaban de hacer notar que hay un error de tipeo en la Guía 3. En el Problema 7, en la definición del operador B faltan coeficientes ‘b’ multiplicando al operador |3><4| y al operador |4><3|. Subí recién una versión con esa correción. Disculpen el error.
nos vemos,
Federico
Hola, les aviso que las clases van a ser, tanto Martes como Jueves, en el Aula 4 del Pabellón 2.
Nos vemos,
Federico